梅花形建筑施工变形精确计算技术

3．2．1 适用于大跨结构安装过程模拟的计算方法

1）正装迭代法

正装法对大跨结构过程进行分析的基本思路为：对实际结构的施工过程进行正序分析，即按照施工方案依次安装各施工步的构件，并施加相应施工步的荷载，来跟踪模拟施工过程中结构的一系列受力状态，从而分析施工过程中结构的内力和变形。正装法可以考虑非线性、混凝土徐变等因素的影响，计算精度高。

正装迭代法计算钢结构施工变形预调值的基本方法为：设计位形作为安装的初始位形，按照实际施工方案对结构进行全过程正序跟踪分析，得到施工成型时的变形，把该变形反号叠加到设计位形上，即为初始位形。类似一般迭代法，若结构非线性较强，基于该初始位形施工成型的位形将不满足设计要求，需要经过多次正装分析反复设置变形预调值才能得到精确的初始位形和各分步位形，进而确定构件的加工预调值和安装预调值。该方法可考虑非线性等因素的影响，计算精度高。

以悬臂梁采用无支撑悬伸施工法的成型过程为例（分三步施工），来说明正装迭代法确定变形预调值的具体步骤（图3-6），其中，v为设计位形，u（i）为第i次迭代过程中结构施工成型时相对初始位形的变形。

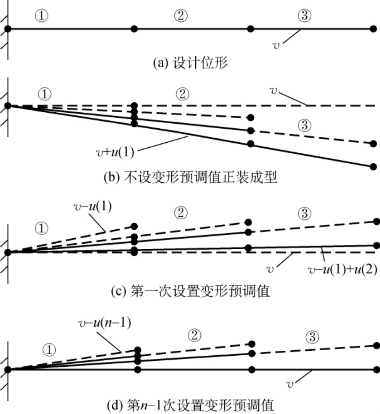
图3-6 正装迭代法计算过程

（1）设计位形v作为施工的初始位形，对结构进行正装跟踪模拟分析，可得到成型状态下结构的变形u（1）和位形v＋u（1）。

（2）利用模型更新功能把变形u（1）反号施加到设计位形上，即把-u（1）施加到设计位形上，就得到初始位形v-u（1）。如果结构的非线性较弱，则以此位形作为初始位形正装成型的位形，使其落到设计位形上或二者的误差u（1）-u（2）满足收敛标准，此时，v-u（1）即为初始位形。

（3）若结构非线性较强，以v-u（1）作为初始位形，正装成型结构变形后将不会回到设计位形，而是将到达新的位形v-u（1）＋u（2），与设计位形的误差为u（1）-u（2）。类似迭代法，需要进行迭代才能得到精确的初始位形。在下一次迭代时，仍以设计位形为基准，在设计位形的基础上施加-u（2），以v-u（2）作为初始位形，正装成型结构的位形为vu（2）＋u（3），与设计位形的误差为u（2）-u（3）。如此反复，直到误差u（n）-u（n-1）满足收敛标准时，得到的位形v-u（n-1）即为精确的初始位形。

（4）以v-u（n-1）作为初始位形，通过正装分析，将得到结构施工的各分步位形以及构件的加工预调值和安装预调值。

2）倒拆迭代法

与正装法不同，倒拆法是对施工过程的逆序分析，主要是分析所拆除的构件对剩余结构变形和内力的影响。分析过程中，在每一步的分析中可考虑非线性的影响，而总的内力和变形采用叠加的方法求解。倒拆迭代法计算钢结构施工变形预调值的基本思路为：根据设计位形，计算最后一施工步所安装的构件对剩余结构变形的影响，根据该变形确定最后一施工步构件的安装位形。以此类推，依次倒退分析各施工步的构件对剩余结构变形的影响，从而确定各构件的安装位形。使得构件按施工正序依次安装完成时结构的位形与设计位形的误差满足要求。以图3-7中的悬臂梁采用无支撑悬伸施工法的成型过程为例，倒拆迭代法计算钢结构施工变形预调值的具体步骤为：

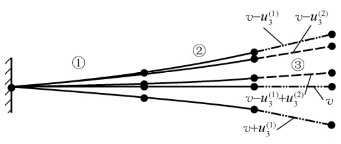
图3-7 杆件3安装位置确定

（1）倒拆迭代法第一步就是要找到杆件3的安装位形，具体步骤（图3-7）为：①在设计位形上，激活杆件1和杆件2，同时把作用在其上的荷载置零，只保留它们的刚度，在此基础上激活杆件3，结构在杆件3的自重作用下会产生变形；②把变形反加到设计位形v上得到位形v-，按此位形重新安装杆件3，若结构的非线性较弱，变形后将落到设计位形v上；③若结构的非线性较强，类似迭代法需要反复迭代才能得到杆件3的安装位形v-使得成型位形与设计位形吻合。

（2）在杆件3安装位形的基础上，即把结构的模型更新为，以杆件3的安装位形为阶段目标位形，确定杆件2的安装位形。具体步骤为：“杀死”杆件3，不考虑杆件3的刚度和作用在其上的荷载。对于已安装的杆件1，不考虑其上作用的荷载，只考虑其刚度，然后安装杆件2。用类似确定杆件3安装位形的方法即可得到杆件2的安装位形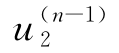（图3-8）。同理，可以得到杆件1的安装位形（图3-9）。

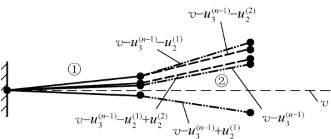
图3-8 杆件2安装位置确定

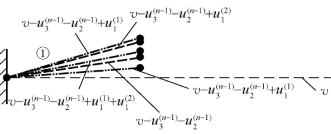
图3-9 杆件1安装位置确定

3）两种方法的优缺点

使用正装迭代法可以考虑非线性、混凝土徐变等因素的影响，计算精度高。但当结构体形复杂、杆件量大时，采用正装迭代法会出现单元漂移过大或发生畸变而导致算法不收敛，最终求解失败。

而采用倒拆迭代法，由于每个施工步都要进行迭代，计算量和工作量都较大，同时难以考虑混凝土徐变等材料非线性的影响。但其对安装过程的模拟思路清晰，求解一般能够顺利进行，对于钢结构这类材料受力表现为典型的线弹性的结构还是非常适用的，因此本书讨论的钢结构安装预控值计算采用倒拆法计算。

3．2．2 大跨度钢结构的非线性有限元理论

前面已经提到，对于使用钢材作为主要材质的大跨建筑，其结构的非线性主要表现为几何非线性而不是材料非线性。对于非线性结构的精确求解，目前通常使用的就是有限元方法，下面根据求解需要对工程结构中典型单元的有限元模型进行简单推导，这类推导可以从有限元相关书籍中查到。最终的求解是使用有限元通用程序来完成。

1）大跨度钢结构建筑施工期变形计算的有限元模型

大跨钢结构的施工过程按不同的结构形式和施工内容可以分成若干个阶段。在每个不同的施工阶段，或者结构形式不同，或者受力体系有所转换，或者是施工荷载发生了变化，而对施工过程中每个阶段的构件位置和内力状况分析计算，是大跨钢结构施工控制中的基本要求。施工控制的主要目的就是确保施工过程中结构安全的前提下，使结构成形状态的构件位置和内力状况最大限度地逼近设计要求。为了实现工程控制的最终目的，有必要在施工过程中预测和监控结构的变形情况和受力状态，这就要求采用精确合理的结构分析方法来计算确定施工过程中每个阶段在受力和变形方面的理想状态，以便了解每个施工阶段的结构行为以及几何线形和内力状况随施工过程变化的全部信息。从这个意义上讲，分阶段施工中结构分析不仅要模拟分段施工过程中结构形成的过程，进行分段施工跟踪计算，而且还要抓住施工阶段结构分析的特点，非线性影响较大和环境影响（如温度和风载）较复杂，选用有效的简化模型和合理的计算方法，为各个施工阶段提供准确的中间目标状态或实际结构状态。考虑上述要求，以下内容是基于非线性有限元理论建立了钢结构施工过程计算的非线性有限元理论与方法。

（1）梁单元

梁单元基本假定：①单元初始形状为一直线，截面沿杆长不变；②单元的应力应变关系符合虎克定律；③单元位移变形为大位移、小应变；④单元变形后仍服从平截面假定；⑤不考虑单元剪切和翘曲变形。

图3-10表示了一个梁元变形过程中三个典型时刻的构形。整个结构的全局坐标系是固定不变的直角坐标系x，单个梁元的局部坐标系始终与固定于梁上的主惯性坐标系rSt重合。采用下面两个假设：

a．假定应力分量σs，σt，τst，与其他应力分量相比可以忽略不计，从而可令σs＝σt＝τst＝0，于是则有σr＝Eerr，τrs＝2Gers，τrt＝2Gert。

b．假定弯曲前垂直于形心轨迹的横截面仍为平面，并且在它们的平面内没有经受应变，但它们不再垂直于变了形的形心轨迹，也即考虑剪切变形的影响。单元可经历大位移、大转角，但假定为小变形。因此，单元的截面积和长度保持不变。梁单元整体坐标系和局部坐标系如图3-10所示。

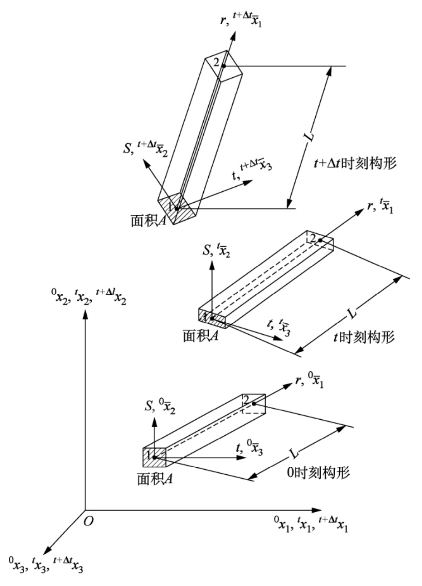
图3-10 梁单元有限元基本假定模型

假定梁单元轴向位移是线性插值（Lagrange插值），两个方向的横向位移均为Hermit插值，用us，ur，ut表示梁中性轴上的点沿局部坐标轴（r，S，t）平动位移，θs，θr，θt表示其相应的转角位移，则单元的位移函数为

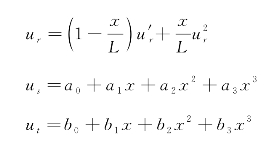
考虑边界条件：

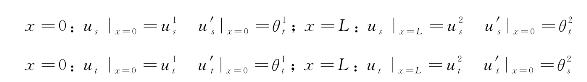
由以上两式可得出的矩阵表达式。

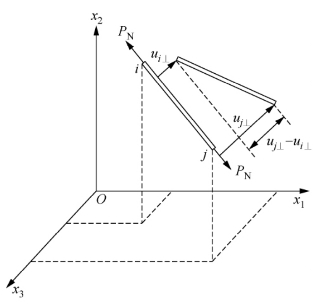
图3-11 杆单元模型

（2）杆单元

杆单元基本假定：①节点为理想铰接节点，杆单元只承受轴向力；②杆单元的应力应变关系符合虎克定律，材料为理想弹性体；③杆单元位移变形为大位移、小应变。

杆单元整体坐标系和局部坐标系如图3-11所示，单元的坐标向量为｛x｝＝｛xi，xj｝T，节点坐标向量为｛xi｝T＝｛xi1，xi2，xi3｝，｛xj｝T＝｛xj1，xj2，xj3｝，单元在局部坐标系中单元节点的位移向量｛ue｝＝｛ui，uj｝T，单元长度L＝单元在当前位置的方向余弦xi2）（xj3-xi3）｝＝｛l m n｝，单元中任一点沿着Xi方向的位移可以表示为

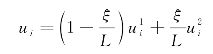
式中，ξ为局部坐标轴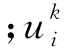为k节点沿Xi方向的位移。(www.zuozong.com)

2）非线性有限元方程的求解方法

用有限元进行结构非线性分析时，其平衡方程最终是一组非线性代数方程

式中，｛u｝表示节点位移；求解非线性方程一般都采用线性方法，即把非线性问题转化为一序列线性问题求解。对于在总荷载作用下进行线性迭代计算的方法，称之为全量迭代方法（简称全量法）。它又可以分成直接迭代法、N-R（Newton-Raphson）迭代法、修正的N-R法等。

3）迭代法的ANSYS实现

ANSYS是一个通用的大型有限元软件，有着种类丰富的单元库，可用于构建结构分析的BIM模型，而且大多数单元都具有被“激活”和“杀死”的功能。通常称这种手段为死活单元功能，对应着EALIVE和EKILL这样两个死活单元的命令。前者使单元参加承载，后者将单元虚设，并不参与结构的承载。EALIVE和EKILL的功能可以描述如下：①“激活单元”是指结构在现有的受力状态下，在结构的某个部位的单元激活，如果结构上未作用新的荷载，原有结构原有的内力和变形不发生变化，而且激活的单元没有任何内力和变形；如果结构上新增加荷载，激活的单元也会产生内力和变形。但由于构件总有重量，因此总会产生新的内力和变形。②“杀死单元”是指结构在某一状态下，某些构件从结构上撤除。这样被撤除构件的内力就反作用于结构上，而使结构发生进一步的内力和变形。

3．2．3 钢屋盖施工过程的变形预控

1）荷载条件

工程实际建设过程中施工步骤、恒荷载大小及其施加次序、施工活荷载、地基沉降、温度作用、风荷载及焊接工艺等诸多因素均会影响结构的力学状态，要精确模拟实际结构的施工过程非常困难。本书综合考虑各种因素的影响，对影响结构受力状态的主要因素（施工步骤、恒荷载、施工活荷载）进行了分析，而对于其他因素（温度作用、风荷载等），因其不是影响施工预调值的重要因素而进行了忽略，这样的假设对评估其对结构受力状态影响不大。

建模的荷载：①计算分步所施加的活荷载按照建筑设计规范施工荷载取值为1．3kN／m2；②计算恒载按结构上部最终完成后屋面板与檩条自重计算为0．7kN／m2（表3-2）。

表3-2 建模荷载条件

2）计算模型

根据施工顺序，首先安装ZHJ-5，ZHJ-6，ZHJ-7，ZHJ-8，PHJ-5，BHJ-5，BHJ-7和BHJ-6，形成一个结构稳定封闭体系（图3-12）。其次沿顺时针方向，依次安装各分区主桁架和边桁架（图3-13）。最终在边桁架BHJ-4位置合拢（图3-14）。

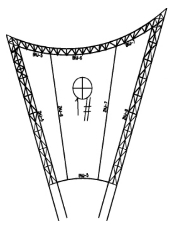
图3-12 第一个封闭花瓣

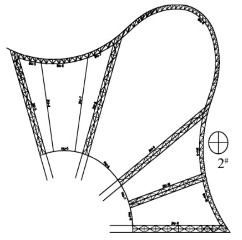
图3-13 顺时针施工

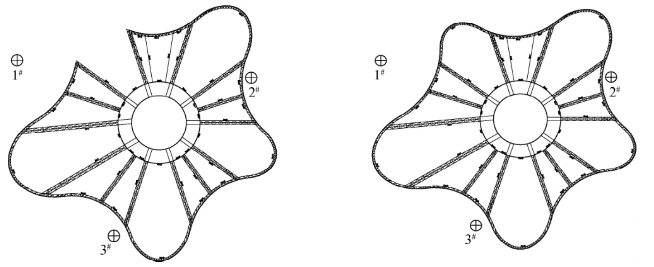
图3-14 最终合拢

建模的假定和条件为：

（1）各构件按截面特性进行赋值。

（2）施工步骤及顺序是先安装主桁架，再安装平桁架及边桁架，待封闭结构形成之后安装网壳。

（3）各施工步所施加的恒荷载，根据拟定的各阶段实际量值确定，并考虑相应阶段的施工活荷载，不考虑温度和风荷载等作用的影响。

（4）支座布置一般按照设计给定的支座条件，当桁架采用分段吊装时，则在分段点处设立竖向支座，该处支座只约束竖向变形，不提供弯曲约束。

（5）面荷载经计算后归并与各控制点成为节点荷载。

（6）计算时先按节点荷载计算沉降后，将沉降量反向迭加到原位再加荷载计算新位移，反复迭代计算直到前后两次迭代的初始位移之差小于0．5mm时停止。

在所有主桁架中位于A区的ZHJ-1和ZHJ-2跨度最大，所组成的“梅花瓣”也最大，因此在本章中将以该A区的主桁架安装预调值计算为例进行详细叙述，详见图3-15～图3-17，其他部位钢结构不在此赘述。

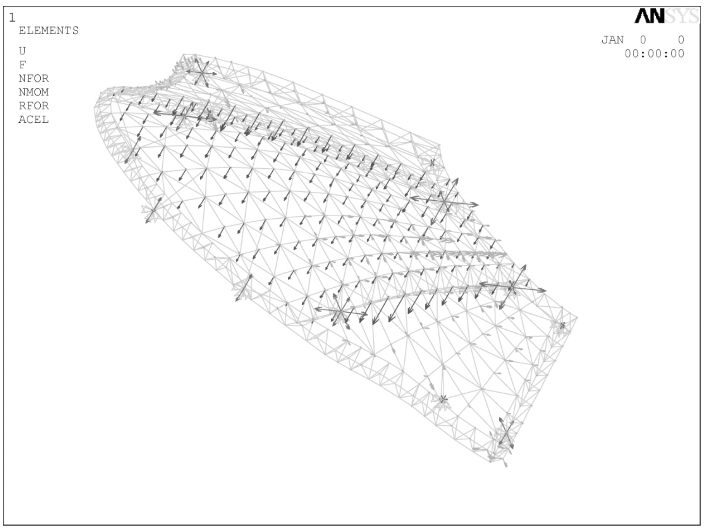
图3-15 A区荷载布置

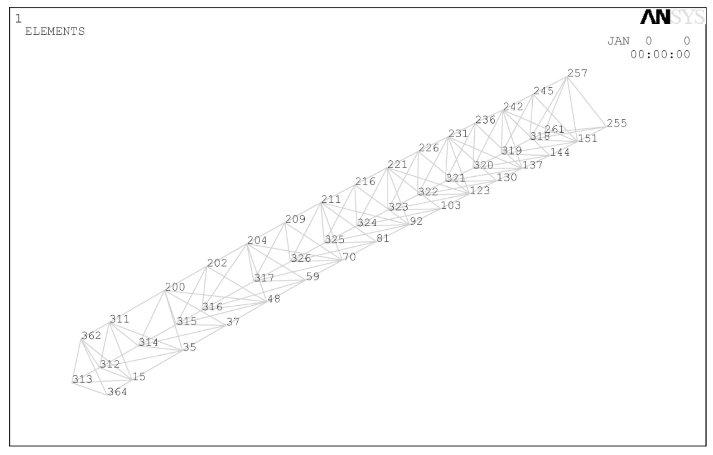
图3-16 桁架ZHJ1节点编号

图3-17 桁架ZHJ2节点编号

3）计算结果

计算结果如表3-3和表3-4所示，预拱变形情况详如图3-18和图3-19所示。

表3-3 桁架ZHJ1各节点预拱值

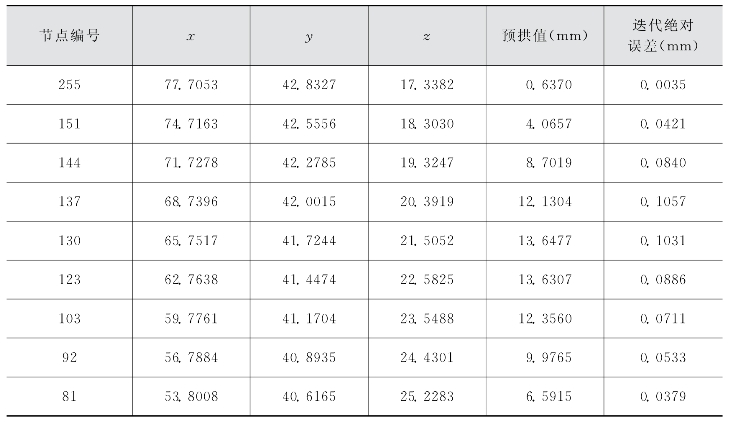
（续表）

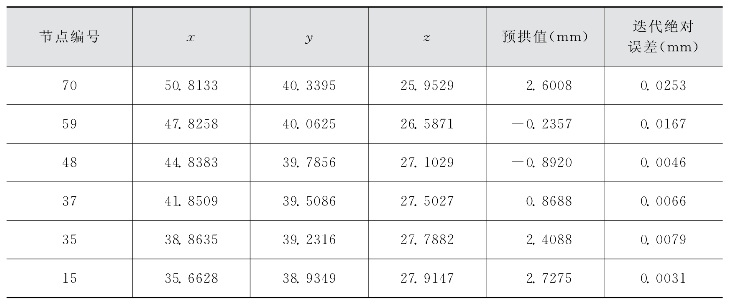
表3-4 桁架ZHJ2各节点预拱值

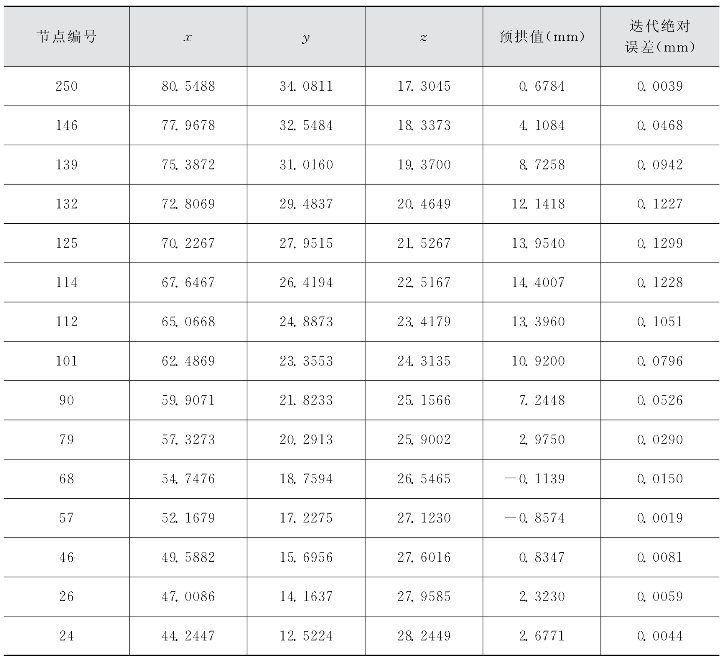
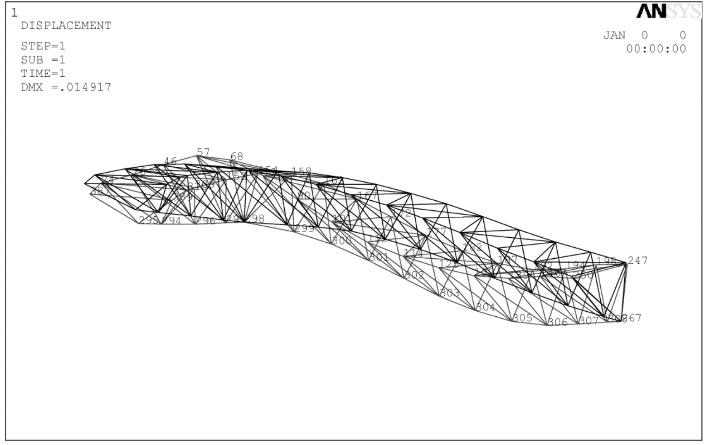
图3-18 桁架ZHJ1预拱变形情况

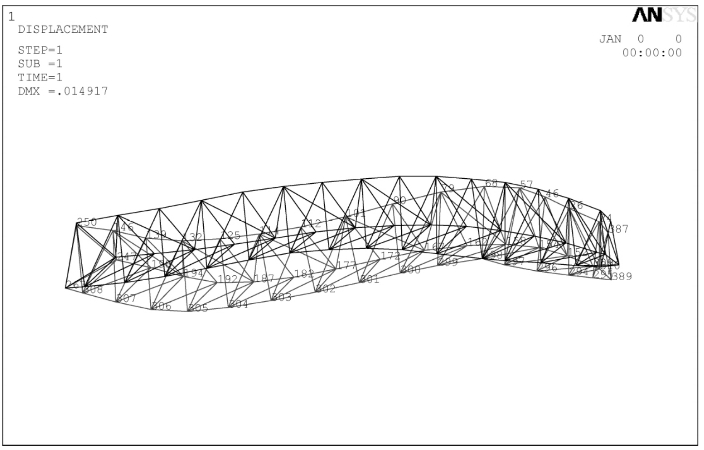
图3-19 桁架ZHJ2预拱变形情况