《汽车涂装技术：红外喷雾可视化和表征的数学处理》

本书中介绍的红外热成像可视化和表征技术是一种采用红外成像来表征和显示液态喷雾的整个流场的光学技术。该技术采用一个经过均匀加热的黑体背景作为热辐射源的发射器，这个发射器也可以看成是一个红外光谱探测器。该方法提供了一个二维图像，其值与强度标上的每个像素值有关。这个数值反映了从喷雾中穿过的光源发射出的红外光谱量子的数量。由于存在喷雾，其光源发出的红外能量将会衰减。

对于一个给定的流体，这种衰减与液滴粒度、喷雾密度和喷雾材料折射率（m=n-ik）有关。红外探测器因为发射强度的衰减而接收到一个减弱信号。这类图像将被记录下来，用以提供一个喷雾衰减图像。利用理论和经验公式进一步处理这个图像即可得出喷雾体积分数、数密度和宏观信息。

5.7.2.1 辐射模型

在本书中，认为喷雾可视化系统包括均匀的或已知强度分布的辐射源和相机或类似的在一定波长范围内可以检测到由任何障碍物引起的辐射强度衰减的设备。辐射强度是指单位时间内的辐射能量转移、立体角、光谱变量和正常的束区。这种辐射能量的传播形式是具有一定波长的电磁波。相机检测到辐射能量的衰减是在其通过参与性介质时，该介质包括由粒度分布确定的液滴所组成的液态喷雾。喷雾是由喷嘴或类似的雾化装置产生的。这一概念的示意图如图5-6所示。

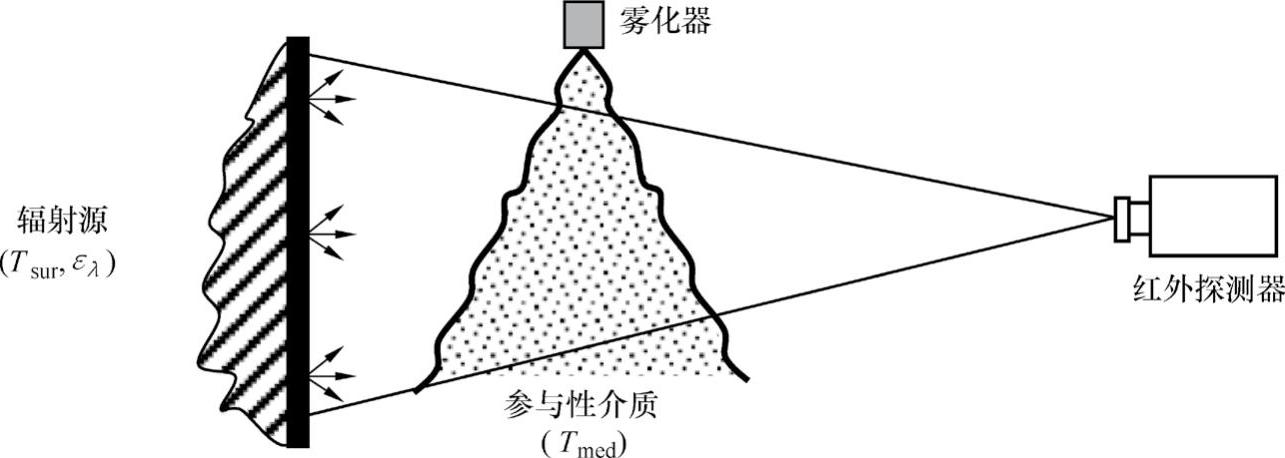
图5-6 红外可视化模型图解

一群液滴的散射和吸收系数，与液滴的数密度以及它们的有效截面面积有直接关系，这些有效面积称为散射和吸收截面（C_scaλ和C_absλ）。一般C_scaλ和C_absλ是粒子取向的函数，复折射率（m=n-ik），与波长有关的粒度和入射光束的偏振。假定大部分的喷雾是由球状液滴组成的，并且与方向无关。同样的，只考虑非偏振光，是因为这有益于多数热传递过程的估算。

考虑到喷雾的微观状态，当电磁波或光量子穿过球状颗粒或液滴的附近时，将被吸住、分散，或是都发生。散射可归因于三个不同的现象，即衍射，颗粒表面的映像和颗粒的折射。图5-7所示为电磁波与球状颗粒之间的相互作用。

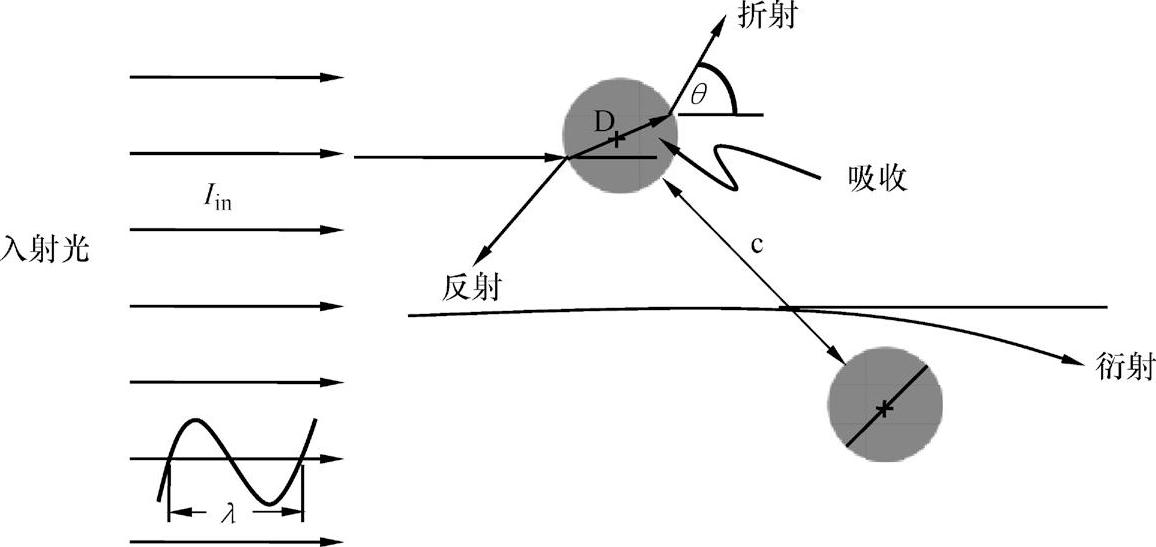
图5-7 电磁波与球状颗粒之间的相互作用

5.7.2.2 红外辐射公式

现在应该把重点放在研究入射的光束与吸收、发射和散射颗粒介质碰撞时的强度I_inλ上。当光束穿过介质时，它的强度由于吸收以及能量折射到其他方向的外散射而下降。光束的强度由于放射物折射到传播方向的内散射或从颗粒中发出的能量而增强。

介质中的强度变化详见以下转移方程式：

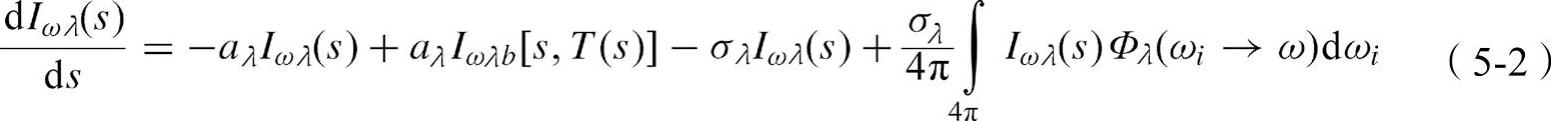
式中，Iωλ是方向光谱强度；s是照射到介质的距离；a_λ与δ_λ分别是吸收和散射的系数。式（5-2）也包括颗粒发出的能量Iωλb，这个能量是根据Planck分布对颗粒温度T的评估，以及ω_i方向变到ω，Ф_λ（ω_i-ω）方向的散射相变。通过下列公式介绍光学浓度τ_λ和散射反照率Ω_λ的定义，即

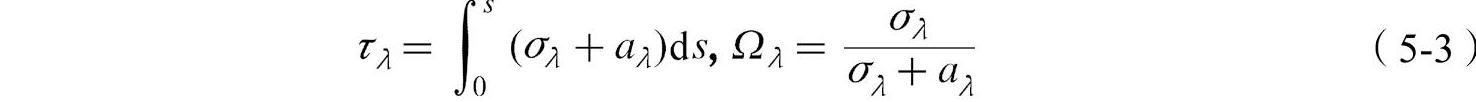
辐射转移方程式（5-2）也可以写成以下形式：

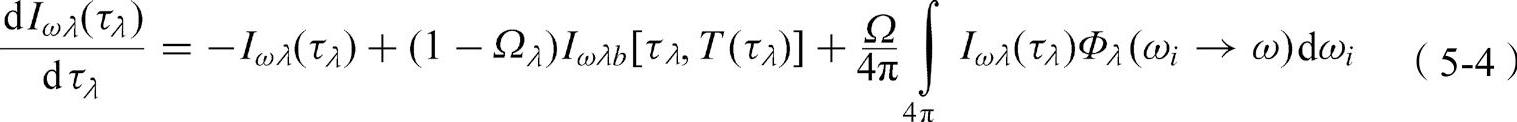
适当提出限制条件是为了公式的完整和高质量。在这一问题中假设所有方向都有明显的边界。主要来源产生的正辐射，可由一个众所周知的散射辐射解释清楚，即

根据其余的分析报告简化假设，即电磁波进入传播方向时的散射和局部散发物可忽略，同样假设这里没有液滴的损失。在分析报告中，气相减少可忽略，在这些假设条件下，式（5-4）中的源项可以被忽略。因此，该式可归纳如下：

用边界条件式（5-5）解式（5-6）得：

这象征着在光程传递过程中传播光束的简单衰弱指数强度，根据式（5-7）可以解决光学密度问题。

因此，传播方向的光学密度可以根据放射强度的衰减计算，而这个衰减是由探测器获取的。

5.7.2.3 二维数字图像分析

获取显示辐射强度减弱的喷雾二维数字图像，经过验证知其是由喷雾液滴的存在所造成的。图像包含一个像素的有限序列p（x，y），其中1≤x≤N_x和1≤y≤N_y，这里的N_x和N_y分别是x和y方向的像素数量。像素的尺寸是ΔxΔy，这里的Δx和Δy，通常始终遍及图像且可能相等（即Δx=Δy），每个像素p（x，y）是微小体积的二维图像φ（x，y），随着内部的有效衰减b（x，y），与喷雾的深度方向相当，在像素的位置，从正常方向到图像p（x，y），与喷雾的深度方向相当。因此，每个减小的体积或三维像素的尺寸可以用ΔxΔyb（x，y）表示（图5-8）。在单个减小体积范围内，存

在一个具有相应液滴粒度分布的有限液滴数量n（x，y）。

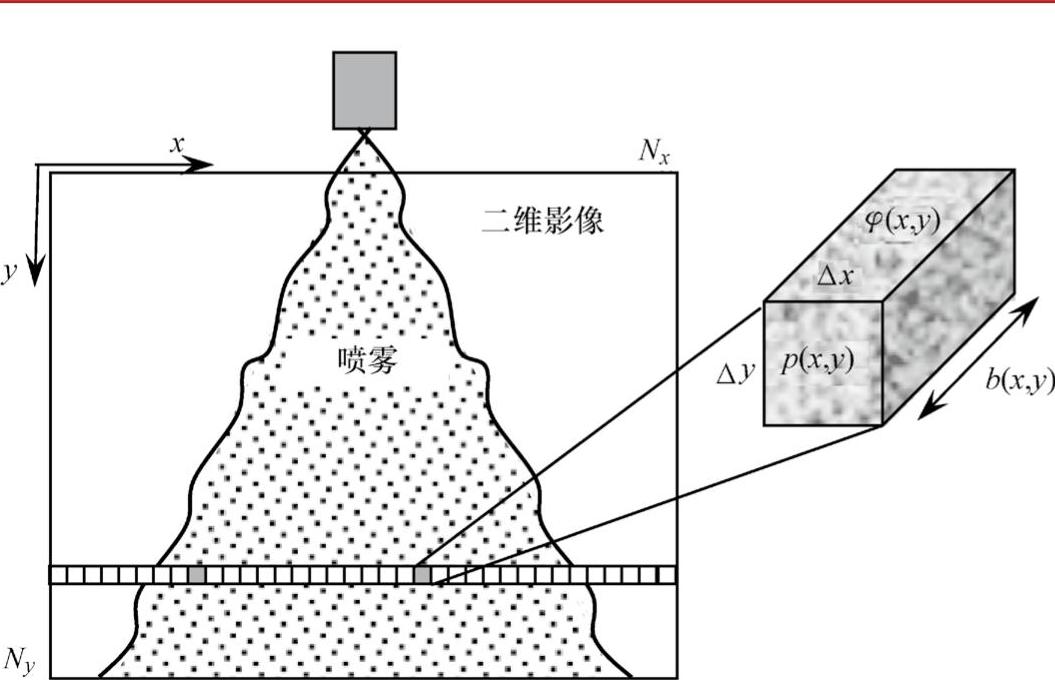
图5-8 喷雾减弱曲线示意图

假设红外能量在喷雾附近空气中的减小可以忽略不计，也就是说，光束的减弱只在衰减量φ（x，y）内发生。式（5-3）中的光学浓度又可以用消光系数κ_λ（x，y）表示成以下形式：

式（5-9）能够将用消光系数表示的光学浓度与物理路径长度统一起来，表示成以下形式：

尽管在集成路径b（x，y）中的液滴展现了粒度分布，而且沿此路径的集中并不均匀，但是有效的消光系数κ_λ（x，y）被认为是独立于液滴粒度分布和液滴浓度的。因此，消光系数可以表示为：

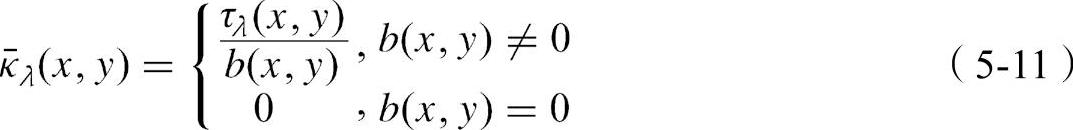
散射和吸收系数分别定义为一个辐射光束每个波段的总能量被散射或吸收的比例。由Tien和Drolen提出的一组粒子（或液滴）的散射和吸收系数与这些粒子（或液滴）的数密度及其有效横截面积有直接联系，这些有效面积称为散射和吸收截面，即C_scaλ（x，y）和C_sabλ（x，y）。

尺寸参数χ定义为液滴周长与光的波长之比，即χ=πD_m/λ。液滴的几何截面积m通过G_m（x，y）=πD²_m（x，y）/4可得。当χ>10时，光散射能通过几何光学近似成消光截面，它是C_scaλ（x，y）和C_absλ（x，y）的总和。这将等同于用物理横截面G_m（x，y）来评估使用基于表面平均液滴尺寸为D₂₀（x，y）的喷雾。因此，在每个像素的图像中，我们得到了G_m（x，y）的值，它包含了整合路径b（x，y）沿衰减量φ（x，y）的相关信息。由此可得：

其中，D₂₀（x，y）的定义如下：

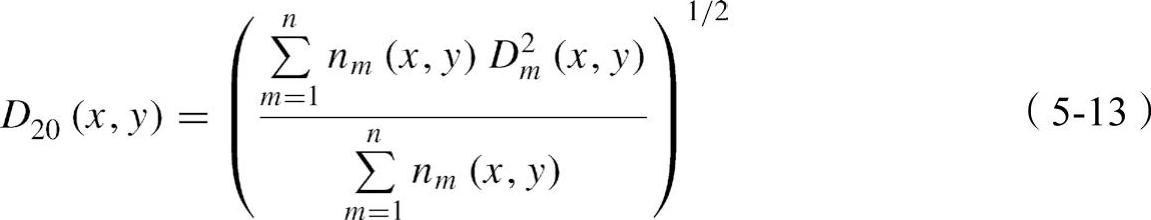
这意味着所有液滴的散射和吸收中所包含的衰减量φ（x，y）等价于等效直径为D₂₀（x，y）的n（x，y）个液滴。

吸收和消光截面可以是液滴无量纲的物理横截面。最终产生的参数由Tien和Drolen提出，称为散射、吸收和消光效率，即

利用上述表示方法，散射和吸收系数可表示成以下形式：

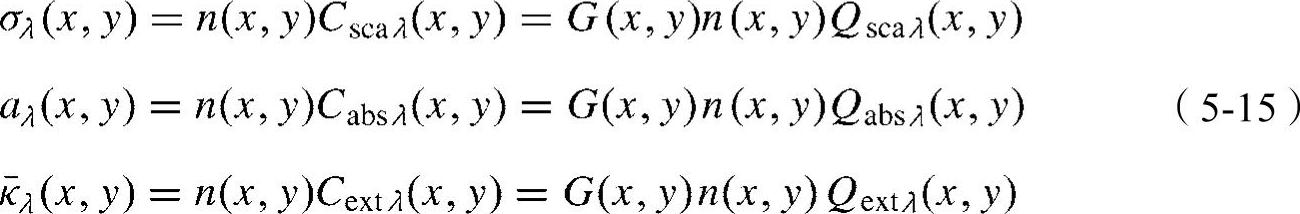
在每个像素[或衰减量φ（x，y）]中，有n（x，y）个液滴具有直径从D_min（x，y）到D_max（x，y）的液滴粒度分布。基于衰减量φ（x，y）内由液滴所占据的总体积的有效直径可定义为

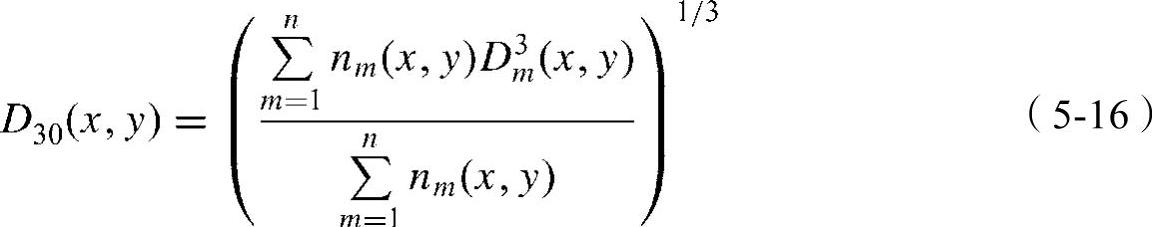
式（5-16）意味着每个控制体积内的液滴体积可由n（x，y）个液滴的当量直径D₃₀（x，y）表示。这些都与该液体在衰减量φ（x，y）范围内的液滴体积分数f_v（x，y）有关。通过式（5-16），体积分数f_v（x，y）可定义为

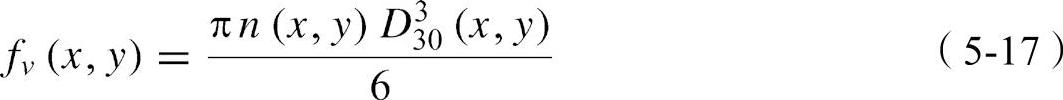
其中，n（x，y）作为单位体积的液滴数量，可表示为(www.zuozong.com)

将式（5-12）中的G（x，y）和式（5-17）中的n（x，y）代入式（5-14）中，可得：

其中，D₃₂（x，y）=D³₃₀（x，y）/D²₂₀（x，y）通常称为表面积力矩平均值或索特平均直径（SMD），它表示面积与体积之比和衰减量范围内的液滴相同的液滴的直径。将（5-13）代入式（5-19）中，则液体体积分数可以依据索特平均直径被定义为

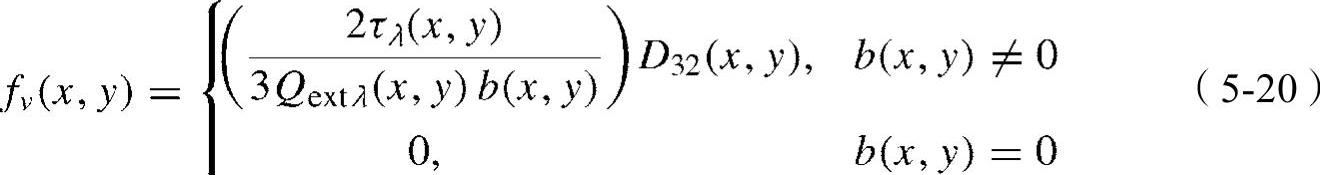
将式（5-16）和式（5-13）中的D₃₀（x，y）和D₂₀（x，y）代入式（5-20），可以得到单位体积的液滴数密度，即

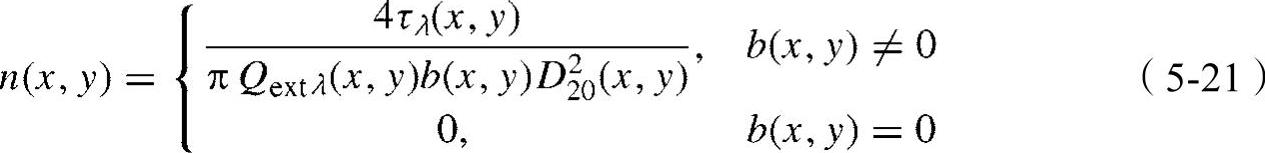
要想算出液滴的数密度和液体体积比例，就需要知道喷雾在每个像素位置的深度b（x，y）和消光效率Q_extλ（x，y）。在计算液滴的数密度时，需要估计D₃₀和D₂₀的值。

5.7.2.4 估算每个像素位置的喷雾深度

红外可视化和表征技术应用于两个汽车自动喷涂工具上，它们分别是高速旋杯雾化器和大容量低压（HVLP）气动雾化器。高速旋杯雾化器产生轴对称喷雾，而HVLP气动雾化器则会产生扇形喷雾。离心力是高速旋杯雾化器的主要雾化机理，HVLP气动雾化器则是利用空气压力实现雾化。b（x，y）是深度方向正常的喷雾图像在每个像素P（x，y）的位置，其计算方法如图5-9所示。如图5-9a所示，高速旋杯雾化器和UCA喷雾具有圆形横截面。如图5-9b所示，HVLP气动雾化器具有椭圆形横截面。对于高速旋杯雾化器和UCA喷雾使用边缘检测方法，沿喷雾图像每个横截面位置的半径R可以通过式（5-22）中的b（x，y）值进行估算。注意，高速旋杯雾化器产生的喷雾起初是具有环形横截面的中空喷雾。但是，喷雾在接近目标表面的过程中，变成具有圆形横截面的固态喷雾。因此，为简单起见，假设为一个圆形横截面。

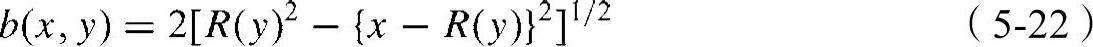
对于HVLP气动雾化器，喷雾的主轴可利用边缘检测方法，根据喷雾每个横截面在图像中的位置估算。图像中的各截面位置。因此，对于HVLP气动雾化器，在每种条件下进行测试时获取两个图像。其中，一个是长轴的图像，另一个是短轴的图像。在获取的图像中，b（x，y）的值可以由式（5-23）计算，即

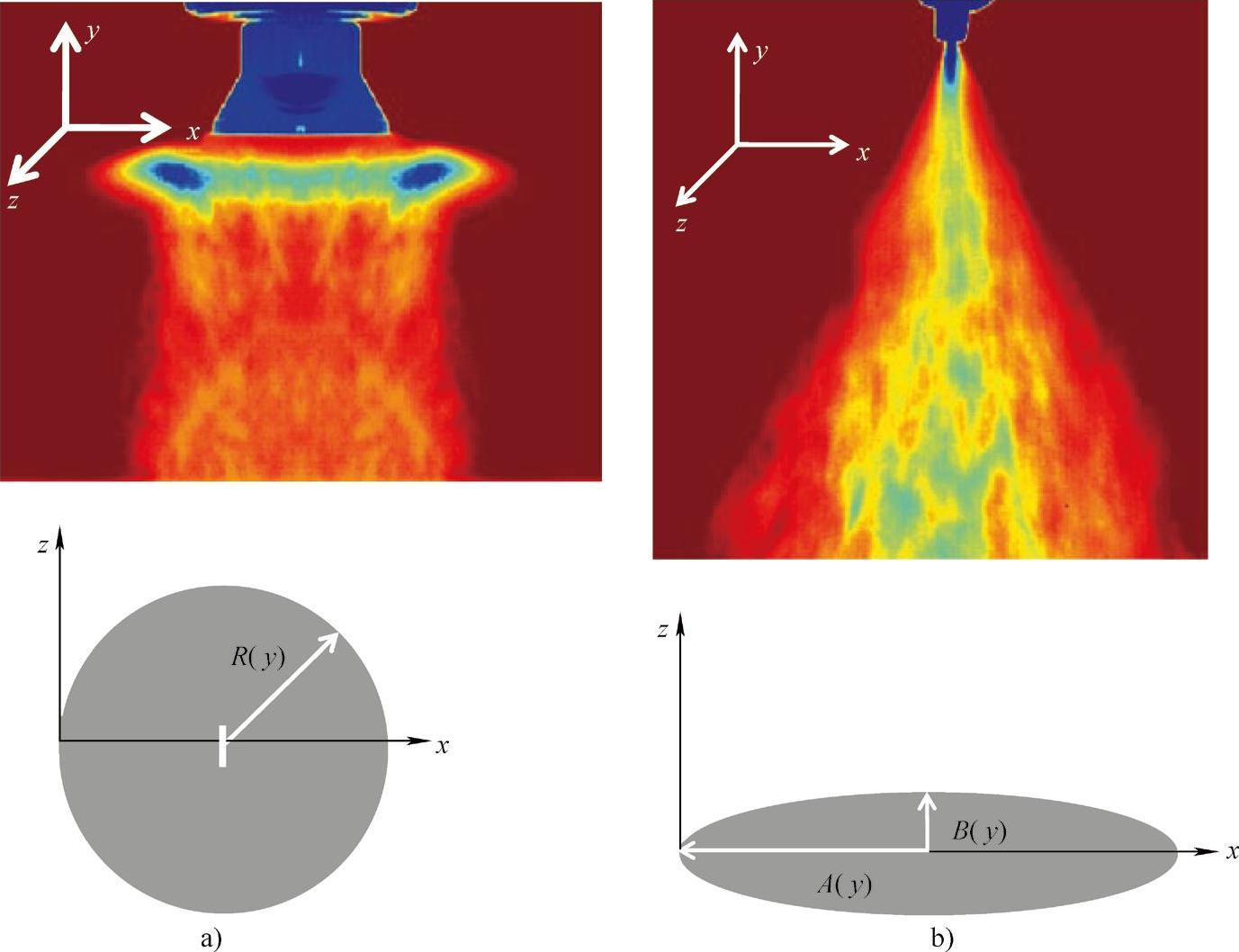
图5-9 计算喷雾深度b（x，y）

a）高速旋杯雾化器和UCA喷雾的横截面 b）HVLP气动雾化器喷雾的横截面

5.7.2.5 消光效率

为了计算消光效率，Matzler的数值解法随之出现。消光效率Q_extλ的表达式为

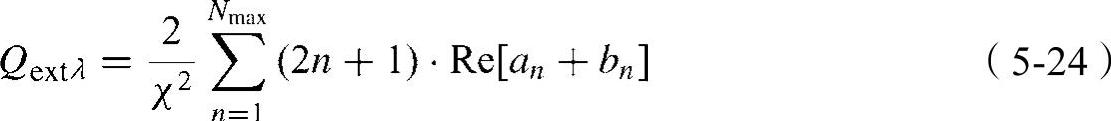
式中，a_n与b_n是三重系数，其定义为

这里ψ_n和ξ_n是黎卡地-贝塞尔函数。

另外，还有

同样散射效率可定义为

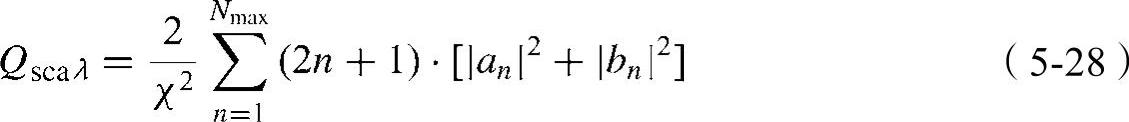
以及通过满足能量守恒而得到的吸收效率为

继Matzler使用MATLAB得到数值解法后，水的米氏效率也通过复折射率1.33+0.00001i得到。水的米氏效率如图5-10所示。用数值解法得到的消光效率（Q_ext）逐渐接近2.1，因此，在分析中假设消光效率的定值为2.1。

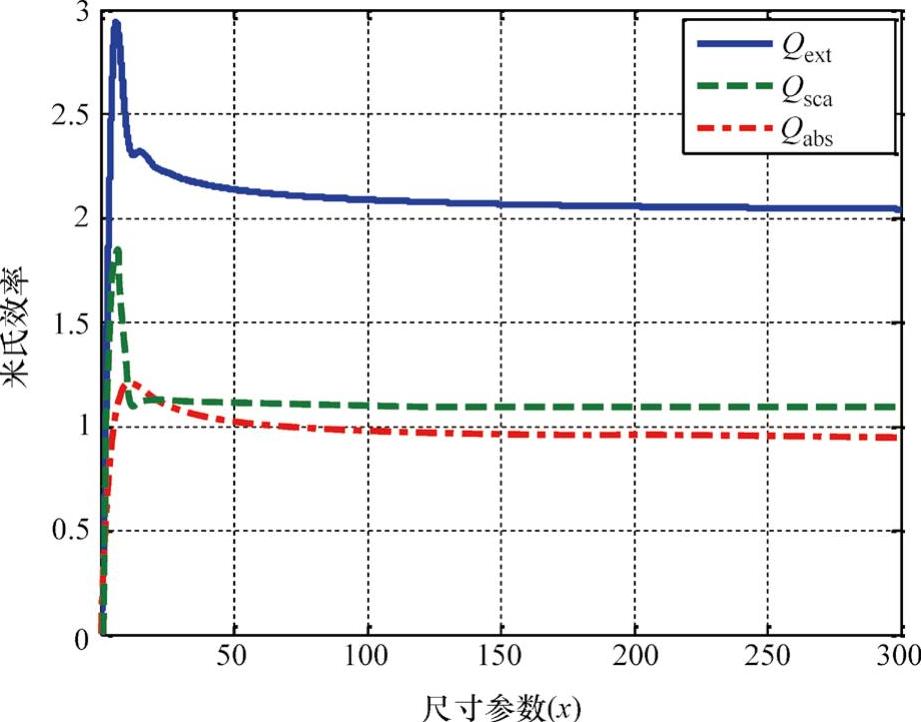
图5-10 水的米氏效率

只要SMD（D₃₂）是已知的，利用得到的米氏消光效率，就可以算出液滴的体积分数。D₃₂值可以通过使用马尔文粒度分析从实验测量中获得。

5.7.2.6 使用经验公式估算D₃₀和D₂₀为了使用式（5-21）计算液滴数密度，我们先使用Nukiyama-Tanasawa分布函数

计算D₃₀和D₂₀。

式中，N是液滴的规范化数量分布；B是常数；C是尺寸参数；q是分布参数；D是液滴直径。B、C和q是通过调整得到的最符合实验数据的常数。Li和Tankin通过使用信息熵找到液滴尺寸的极限是零到∞，随后发现了分布函数，即

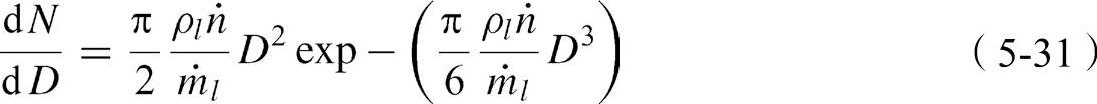
式中，l是液体密度；m·_l是液体的质量流率；n是单位时间内的液滴数密度。

这是Nukiyama-Tanasawa分布函数的一种形式，其中分布参数（q）不再是一个自由变量，而是等于3。

通过定义SMD从而给出以下定义：

将式（5-31）代入式（5-32），得到由液体密度、液体的质量流率和单位时间液滴

数密度所形成的SMD的表达式为

同样从式（5-16）中D₃₀的定义，得到由液体密度、液体的质量流率和单位时间液滴数密度所形成的D₃₀的表达式为

根据式（5-34）和式（5-33），得到通过D₃₂表示的D₃₀的公式。只要D₃₂可以从实验测量中得到，就可以利用这个公式得到D₃₀的值。

同样D₂₀从它的定义（式（5-13））求解，得到：

若用D₃₂表达D₂₀和D₃₀，则只需知道D₃₂的值就可以通过这些数学关系估算D₂₀和D₃₀的值。液滴数密度可以使用式（5-21）得到。