土力学中的有效应力与土体压缩和强度关系的解析

在一般情况下，土的孔隙中含有水和空气。设土中微单元体的截面面积A（包括土粒和孔隙的总截面面积）上作用着法向力p，如图3-16所示，则由固体颗粒、孔隙中的水和气体共同承担的总应力为δ=P/A。与土体压缩和强度有关的只是土粒接触面上的应力，而非颗粒截面上的应力，然而，粒间接触面的方位却是随机的。这样，考虑通过接触面传递的应力时，就只能取微单元体中平行于面积A的统计接触面总面积A_s，并设其上由P引起的法向力和切向力为P_s和T_s。相应的粒间接触面上的法向应力和切向应力为σ_s=P_s/A_s和τ_s=T_s/A_s。粒间应力的定义是σ_g=P_s/A，如引入接触面积比a=A_s/A，则σ_g=σ_sA_s/A=σ_sa，这就是总应力σ中起着控制土体体积变化和抗剪强度的有效应力σ′，即

σ′=σ_g=σ_sa （3-48）

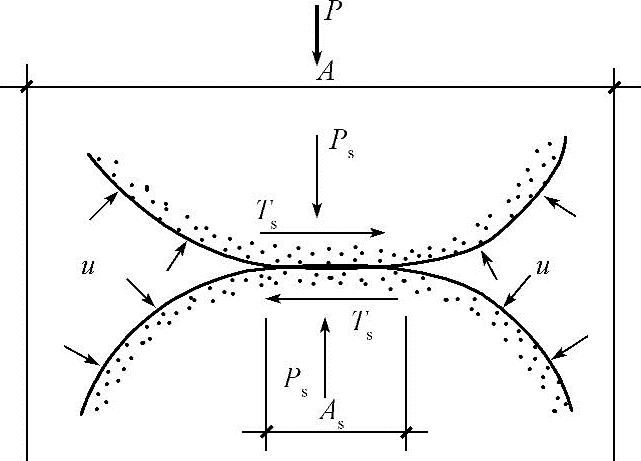
图3-16 有效应力原理

对具有普遍意义的非饱和土，孔隙压力包括孔隙水压力u_w和孔隙气压力u_a两个分量。如何确定有效应力σ′与σ、u_w、u_a之间的关系是土力学的基本问题之一。毕肖普对饱和度不太小（S_r=40%～85%）的非饱和土提出了土中有效应力的表达式，即

σ′=σ-[u_a-χ（u_a-u_w）] （3-49）

式中 χ——与土的饱和度有关的参数。当饱和度S_r=100%，χ=1时，上式简化为太沙基凭经验得到的饱和土的有效应力表达式为

σ′=σ-u(www.zuozong.com)

或 σ=σ′+u （3-50）

式中 u——饱和土的孔隙压力，即孔隙水压力u_w。

斯肯普顿在试验基础上对以上两式作出了详细的论证。对无黏性土，其推理是简单的：由于孔隙压力各向相等，根据微面A的法向平衡条件即得

P=P_s+（A-A_s）u=σ_sA_s+（A-A_s）u （3-51）

以A除上式各项，得

σ=σ_sa+（1-a）u=σ′+（1-a）u （3-52）

式中接触面积比a＜0.03，可以略而不计，因此式（3-50）成立。对黏性土，其中黏土矿物颗粒为结合水所包围，实际上并不直接接触，式中的有效应力应认为是粗颗粒的接触面应力和细颗粒之间的分子力的综合效应。