二、三维成形法在汽车变速器设计中的应用

（一）几何原理

液力变矩器工作轮的叶片一般都是空间扭曲的，叶形设计首先需要保证能对叶片的真实长度、厚度和角度等参数进行正确的描述。本文提出的三维成形法主要通过两次转换实现对叶形的定义：

1）利用平行的翼面层对叶片进行切分，使得对空间叶形的描述可通过对各翼面层上叶片断面形状的描述来实现，从而将空间曲面转化为空间曲线。例如，在图10-21中，叶片被五个翼面层（0，1/4，2/4，3/4，1）切分，叶形可以由各翼面层上的叶片轮廓线确定。

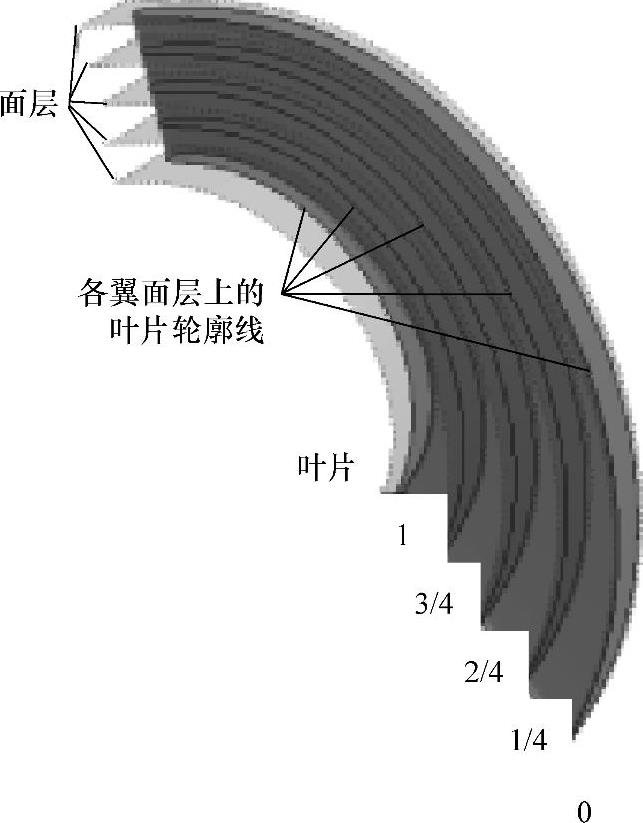
图10-21 叶形空间描述

2）利用投影于多圆柱面的等倾角射影法，将翼面层上的叶片轮廓线转化为平面叶形，从而将空间曲线转化为平面曲线，等倾角射影得到的展开线可与原曲线保持相等的长度和倾角。图10-22为翼面层0上叶片骨线的等倾角射影图。传统的叶片设计方法中也用到了等倾角射影法，但是它主要考虑的是进出口角，对于中间变化过程则多依赖于经验进行手工绘形，其设计过程繁琐且精度低。三维成形法通过对骨线上各点叶片角和厚度的定义，根据空间几何关系，可直接生成叶片表面点的三维坐标，进而生成叶片的三维模型，不仅保证了空间叶形的精确性，而且可以对叶形进行参数化定义和研究。

图10-22 多圆柱面上的等倾角射影图

参照图10-22，定义骨线上各点的位置参数如下：

x、y、z——X、Y、Z轴坐标值；

r——半径；

θ——绕Z轴从X轴到Y轴方向的旋转角度；

β——叶片角；

m——沿子午曲线的距离；

s——沿曲线的距离百分数（0≤s≤1，进口侧为0，出口侧为1）；

c——曲线真实的三维长度。

各参数的几何关系如下

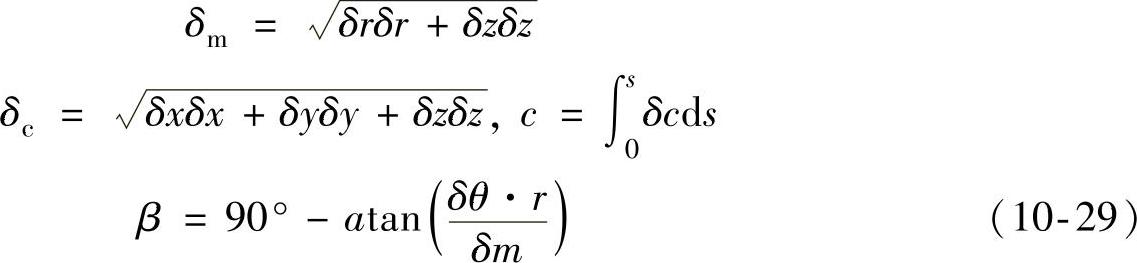
于是，在划分了翼面层之后，叶片骨线形状便可以通过角度参数θ得以确定，叶片加厚时，则将相应点沿骨线的垂直方向偏移厚度值的1/2即可。处理叶片前、后缘时，还需定义圆角半径以得到合理的叶形，得到各翼面层叶形后，通过直纹面将其连接起来，从而生成叶形的三维模型。

（二）设计过程

三维成形法的具体设计流程如图10-23所示。一般情况下，划分两个或三个翼面层来确定叶形就已经足够了，即确定外环和内环或增加中间翼面层上的叶形角度和厚度分布规律。

在设计叶片角度规律时，θ曲线是最基本的空间位置定义，但叶片设计中更能体现与性能之间关系的是叶片角β。因此，以叶片角来描述叶形的角度规律更加直观有效，在设计了合理的叶片角变化规律后，叶片在翼面上的形状就被确定下来了，而叶片在翼线方向上的倾角可通过整体偏移θ曲线来调整。叶片角曲线应保持变化平缓，以保证叶形平顺。

厚度分布规律主要遵从保证过流面积尽量一致的原则，设计中可使用变矩器叶片厚度分布的统计数据，也可采用一些成熟的叶形厚度分布规律，如NACA（美国国家航空咨询委员会）叶形系列和儒可夫斯基叶形等，实际设计中应根据需要进行细节上的调整。

（三）叶形参数研究

作为研究对象的变矩器，其基本角度参数见表10-1，为了保证叶片基本角度参数不变，划分三个翼面层来定义叶形，由此可直接对中间翼面上的叶形角度参数进行控制。为了防止叶形扭曲，内、外环上的叶片角变化规律设计成与中间翼面一致，后文中描述各叶片角变化规律时，仅给出中间翼面上的叶片角变化规律。

1.泵轮

用来作对比研究的三种泵轮采用同样的厚度变化规律，如图10-24a所示，外环即翼面层1/2上的叶片弦长较长，最大厚度较大，约为4.3mm；内环即翼面层1上的叶形相对较薄，最大厚度为3mm，整个叶片的厚度分布规律保持一致。为了便于分析，三种泵轮的叶片角变化规律采用了比较特殊的三种方案，如图10-25b所示，其中泵轮B为直线型，是进行对比研究的基本形式。将叶片角从进口到出口沿弦线方向积分，可得到叶片出口边缘相对于进口边缘的角位移，采用图10-25b中的三种方案可保证叶片进出口的相对角位移相同，从而使得所进行的性能对比仅仅受到叶形的影响。

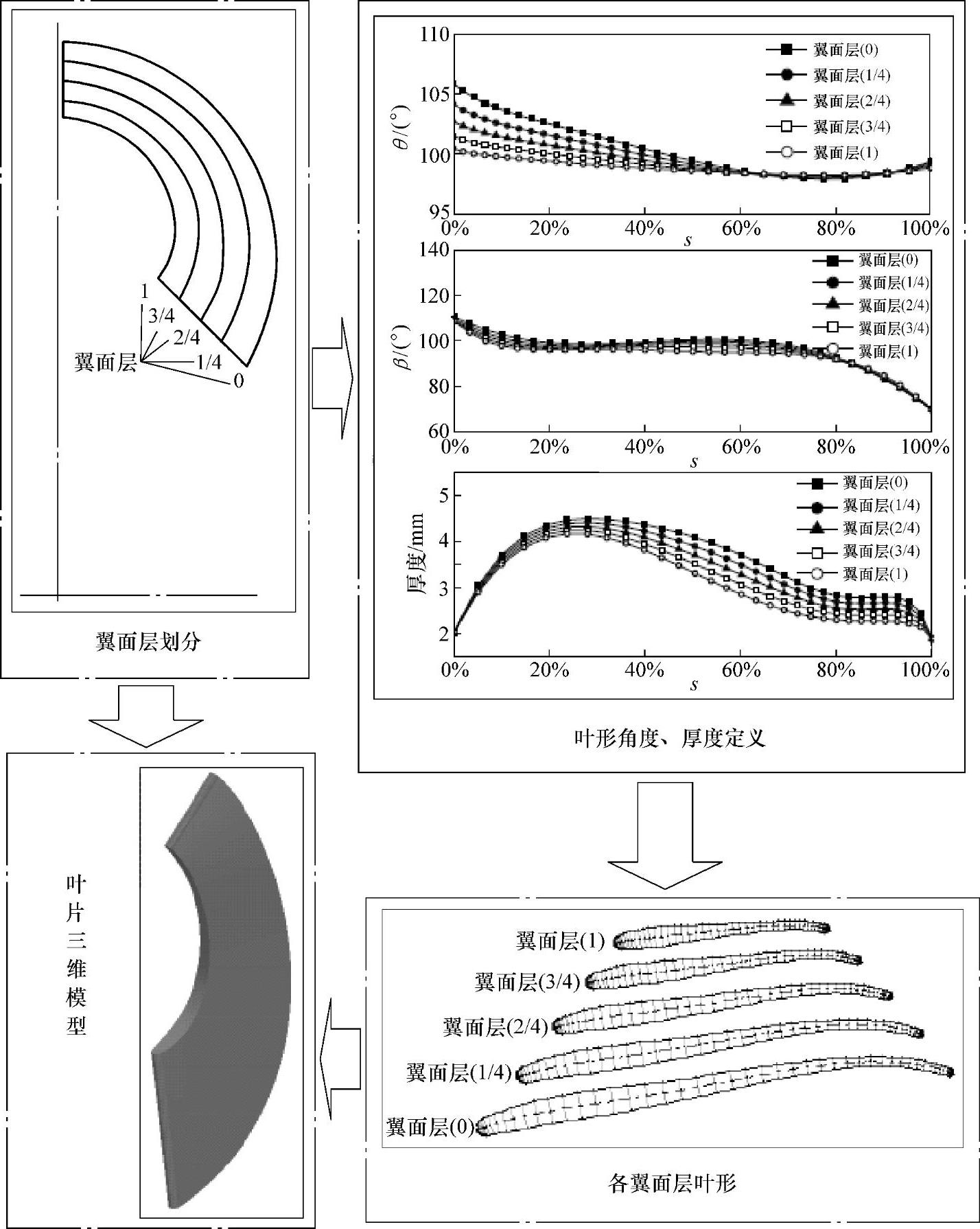
图10-23 三维成形法设计流程

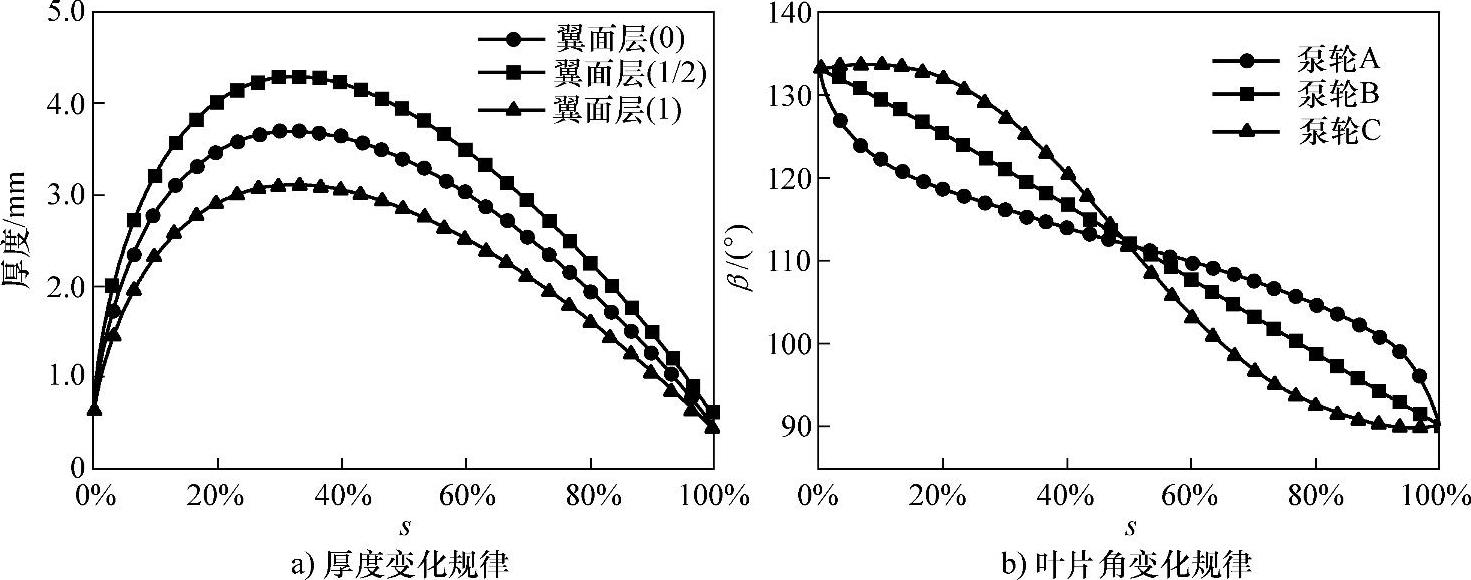
图10-24 泵轮叶片参数(www.zuozong.com)

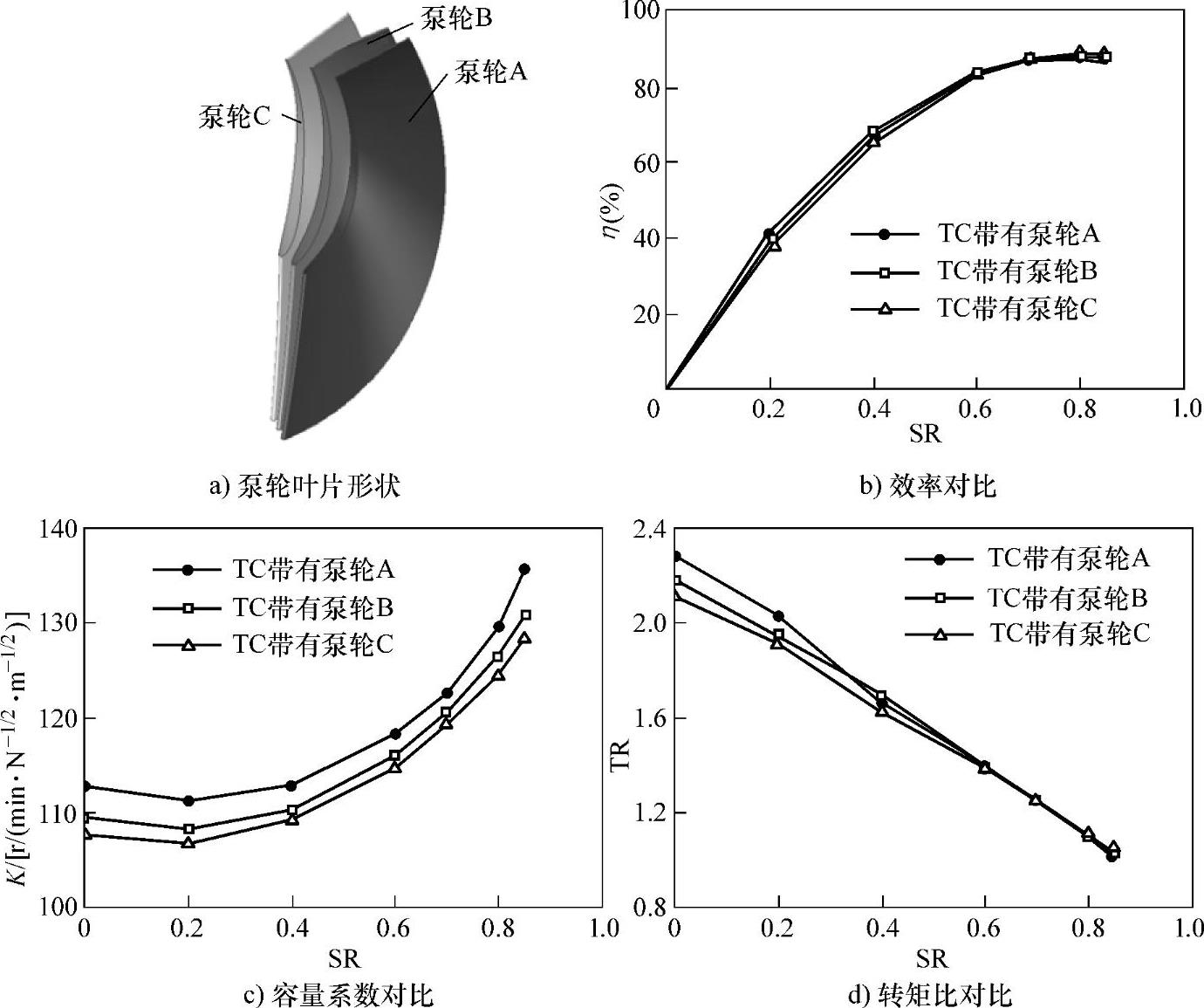
图10-25 泵轮叶片角变化规律研究

三种泵轮的叶片形状如图10-25a所示，将三种泵轮分别与同样的涡轮和导轮搭配组合成三种变矩器，所搭配的涡轮和导轮的叶片角变化规律均为直线型。在对涡轮和导轮进行对比研究时也采用同样的方法，三种变矩器的效率、泵轮容量系数、转矩比的对比情况如图10-25b、c、d所示。

由图可知，效率性能上，泵轮C所对应变矩器的最高效率最高，泵轮A所对应变矩器的最高效率最低，但最高效率变化值不大；泵轮容量系数K的对比显示，泵轮C所对应变矩器的泵轮容量系数最小，泵轮A的最大；在转矩比方面，泵轮A所对应变矩器的起动转矩比最大，泵轮C所对应变矩器的起动转矩比最小。

可见，对泵轮采用前后缘变化平缓、中间变化剧烈的叶片角变化规律（如泵轮C），可获得较高的效率性能，相应的泵轮容量系数也较小；采用前后缘变化剧烈、中间变化平缓的叶片角变化规律（如泵轮A），可获得较大的起动转矩比，泵轮容量系数较大；叶片角变化规律为直线型的泵轮，其各项性能均介于上述两种泵轮之间。

2.涡轮

三种涡轮采用同样的厚度变化规律，如图10-26a所示。外环即翼面层0上的叶形最大厚度约为8mm，内环即翼面层1上的叶形最大厚度约为4mm，整个叶片厚度分布规律保持一致。与泵轮类似，三种涡轮的叶片角变化规律采用了比较特殊的三种方案，如图10-26b所示，其中涡轮B为直线型，是进行对比研究的基本形式。

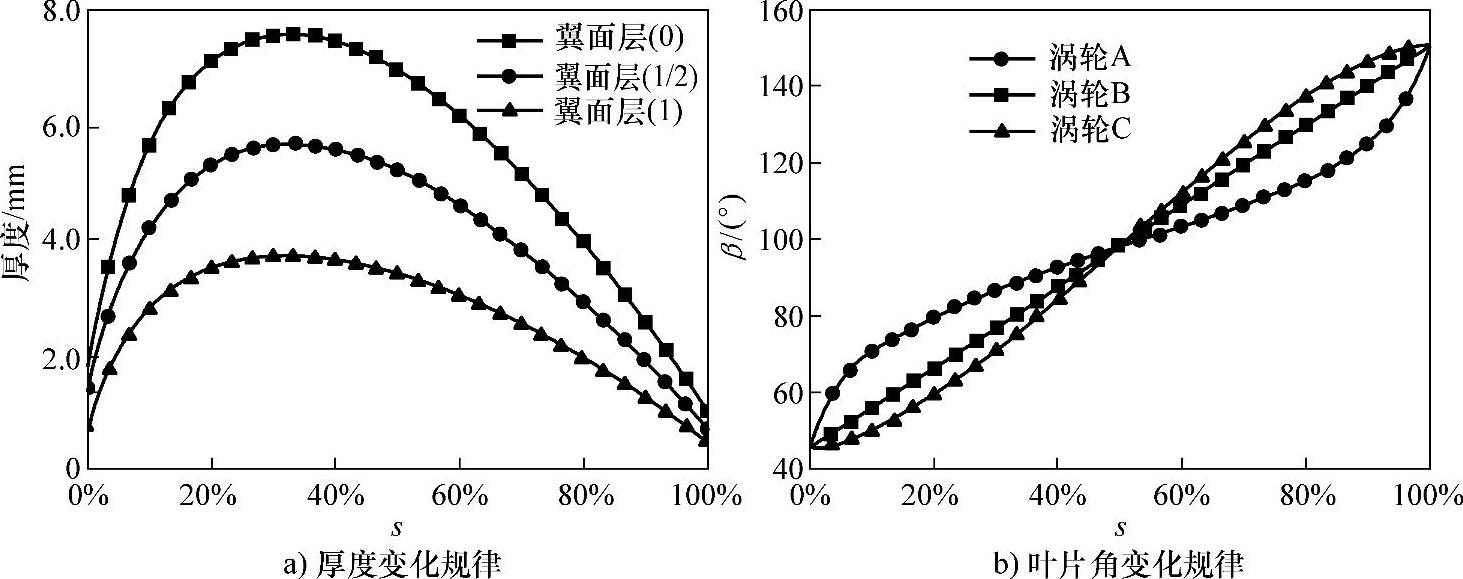
图10-26 涡轮叶片参数

三种涡轮的叶片形状如图10-27a所示，将三种涡轮分别与同样的泵轮和导轮搭配组合成三种变矩器，其效率、泵轮容量系数、转矩比的对比情况如图10-27b、c、d所示。

效率性能上，涡轮C和涡轮B所对应变矩器的最高效率最高，涡轮B所对应变矩器在高效点临近工况下的效率比涡轮C要高，涡轮A所对应变矩器的最高效率最低；泵轮容量系数K的对比显示，涡轮C所对应变矩器的泵轮容量系数最大，涡轮A的最小；在转矩比方面，涡轮C所对应变矩器的起动转矩比最大，涡轮B与其相差不大，涡轮A所对应变矩器的起动转矩比最小。

由以上分析可知，对涡轮采用前后缘变化平缓、中间变化剧烈的叶片角变化规律（如涡轮C）或者采用直线型叶片角变化规律（如涡轮B），均可获得较高的效率性能，同时可保证较大的起动转矩比，前者泵轮容量系数较大；采用前后缘变化剧烈、中间变化平缓的叶片角变化规律（如涡轮A）可获得较低的泵轮容量系数，起动转矩比较小。

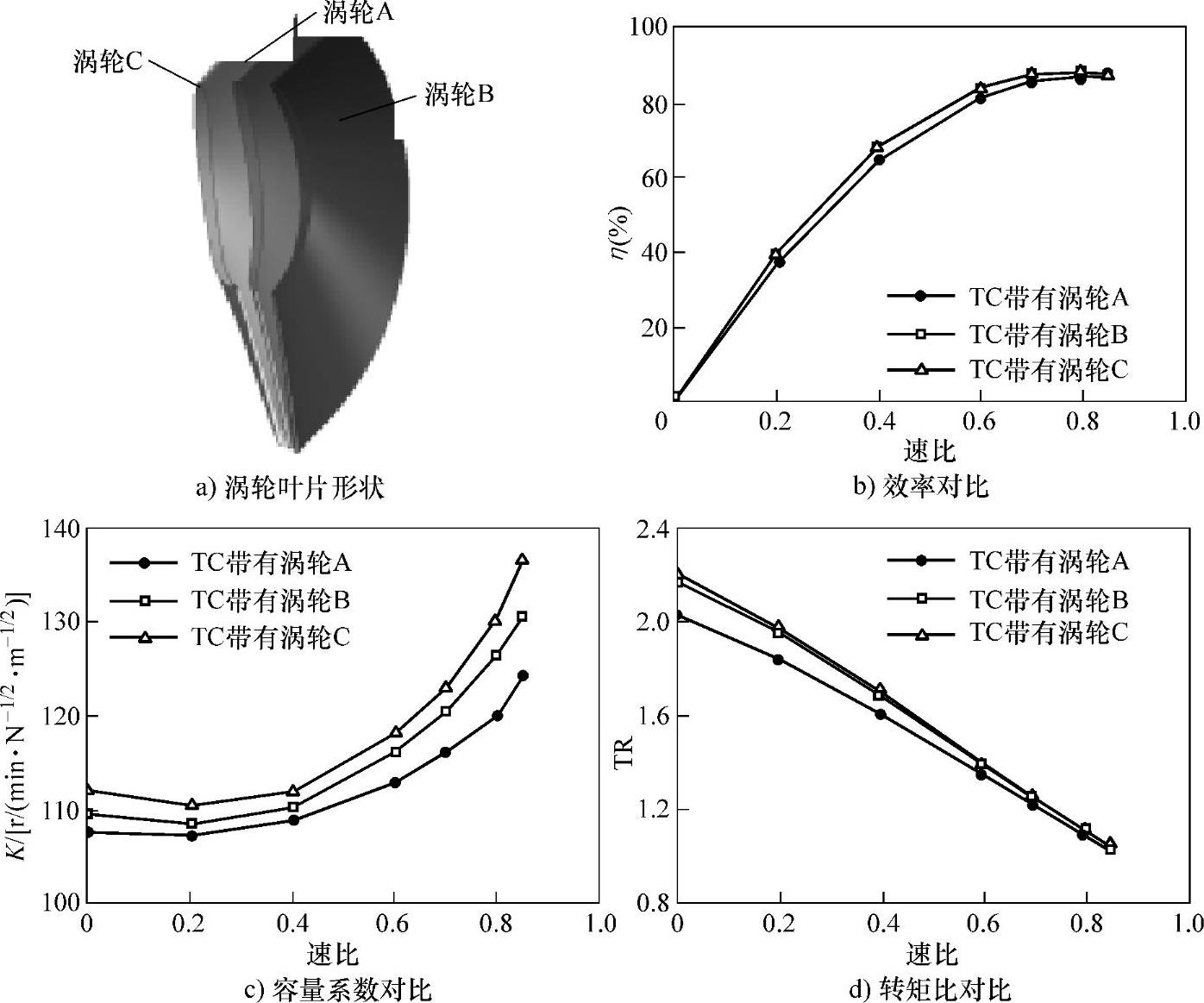
图10-27 涡轮叶片角变化规律研究

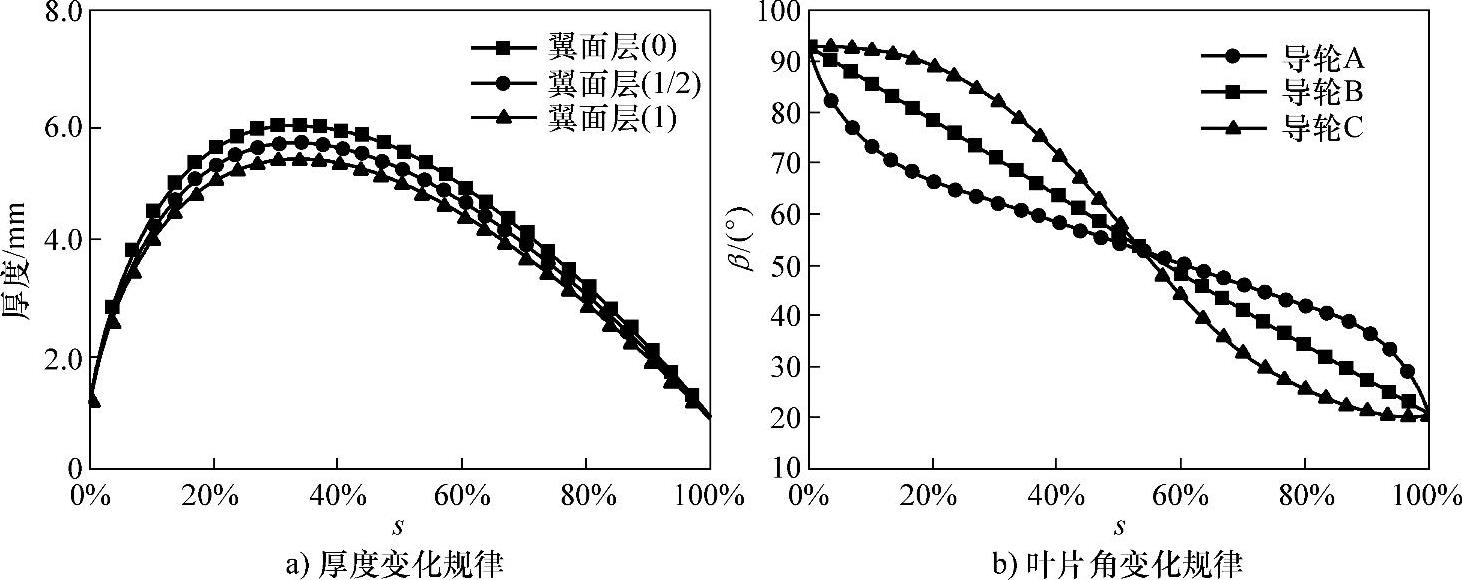
图10-28 导轮叶片参数

3.导轮

三种导轮采用同样的厚度变化规律，如图10-28a所示。外环上的叶形最大厚度约为6mm，内环上的叶形最大厚度约为5.4mm，整个叶片厚度分布规律保持一致。与泵轮类似，三种导轮的叶片角变化规律采用了比较特殊的三种方案，如图10-28b所示，其中导轮B为直线型，是进行对比研究的基本形式。

三种导轮的叶片形状如图10-29a所示，将三种导轮分别与同样的泵轮和涡轮搭配组合成三种变矩器，其效率、泵轮容量系数、转矩比的对比情况如图10-29b、c、d所示。

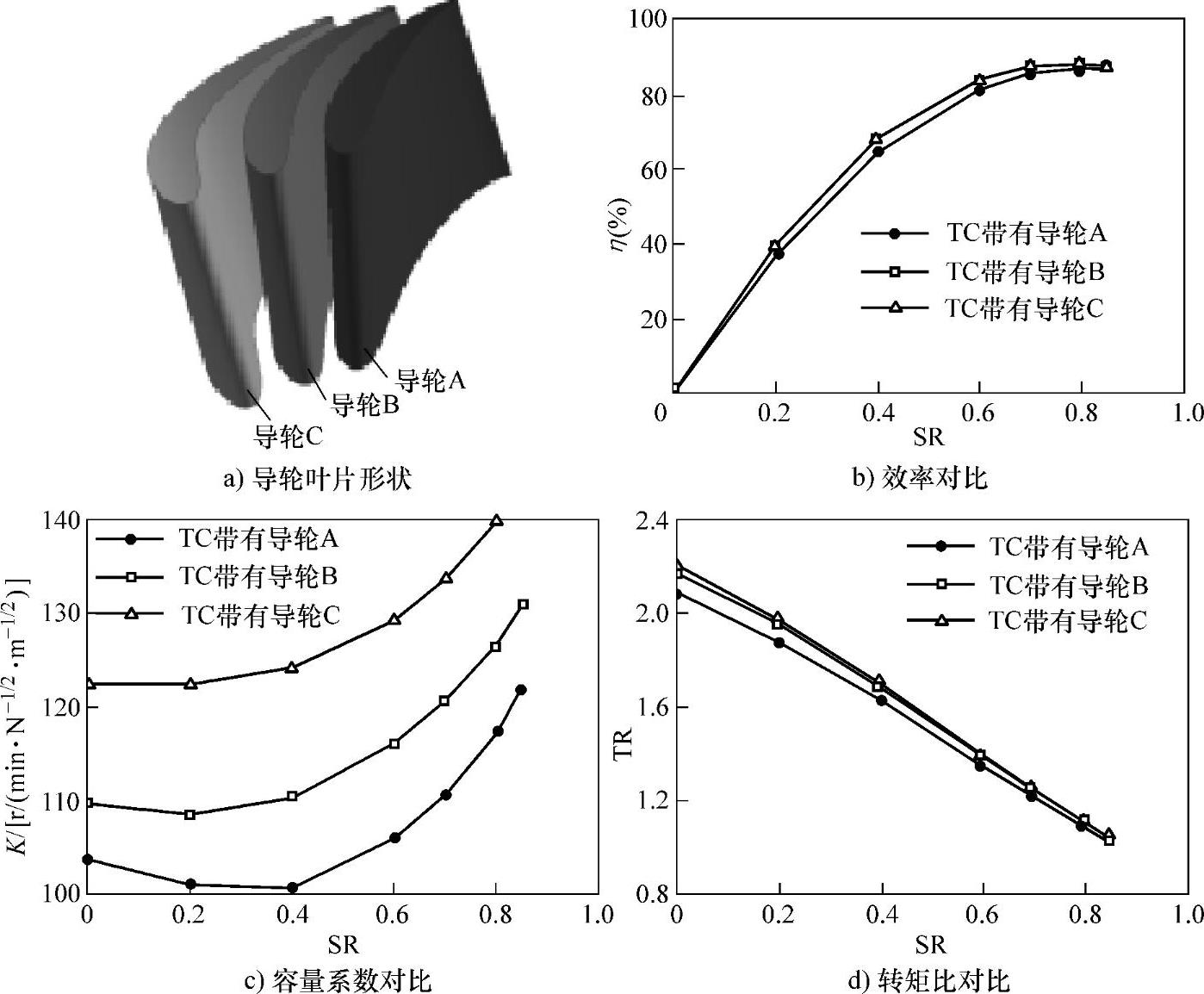
图10-29 导轮叶片角变化规律研究

SR—速比

效率性能上，导轮B所对应变矩器的最高效率最高，导轮C所对应变矩器的最高效率最低；泵轮容量系数K的对比显示，导轮C所对应变矩器的泵轮容量系数最大，导轮A的最小；在转矩比方面，导轮C所对应变矩器的起动转矩比最大，导轮B与其相差不大，导轮A所对应变矩器的起动转矩比最小。

由以上分析可知，对导轮采用直线型叶片角变化规律（如导轮B），均可获得较高的效率性能；采用前后缘变化剧烈、中间变化平缓的叶片角变化规律（如导轮A），可获得较小的泵轮容量系数，起动转矩比也较小；采用前后缘变化平缓、中间变化剧烈的叶片角变化规律（如导轮C），则可获得较大的起动转矩比。

4.结论

1）要提高变矩器的最高效率，可采用的方案有：泵轮采用前后缘变化平缓、中间变化剧烈的叶片角变化规律；涡轮采用前后缘变化平缓、中间变化剧烈的叶片角变化规律；导轮采用直线型叶片角变化规律。但总的来说，通过改变叶片角变化规律来调整变矩器效率的效果并不明显，更为有效的方法仍然是改变叶片进出口角等基本参数。

2）要降低泵轮容量系数，可采用的方案有：泵轮采用前后缘变化平缓、中间变化剧烈的叶片角变化规律；涡轮采用前后缘变化剧烈、中间变化平缓的叶片角变化规律；导轮采用前后缘变化剧烈、中间变化平缓的叶片角变化规律。对比发现，导轮叶片角变化规律对泵轮容量系数的影响最大，起动工况下，泵轮容量系数K₀的最大变化可接近20r/min·N^-1/2·m^-1/2，而泵轮和涡轮对其影响相对较小。因此，通过改变导轮叶片角变化规律，可以在很大范围内调整泵轮容量系数，这一方法比目前使用较多的泵轮出口尖端弯曲方法更容易保证其他性能参数的稳定性。

3）要增大起动转矩比，可采用的方案有：泵轮采用前后缘变化剧烈、中间变化平缓的叶片角变化规律；涡轮采用前后缘变化平缓、中间变化剧烈的叶片角变化规律；导轮采用前后缘变化平缓、中间变化剧烈的叶片角变化规律。

基于上述结论，并综合考虑变矩器设计任务书的要求，本文对W30原型进行了改型设计，在上述讨论过的叶形参数变化规律上进行了局部调整，最终获得了满足要求的变矩器性能。

本节所进行对比研究的叶片角变化规律仅仅是几种特殊情况，而厚度变化规律也只是采用了经验数据，实际设计工作中，应根据具体设计目标寻求最优的变化规律。由于叶片参数的变化规律可以是任何形状，而各叶轮之间又存在相互影响，因此，深入细致地研究叶片参数对变矩器性能的影响将是大量而长期的工作。