非线性系统动态分析：《系统工程》

1)非线性系统的动态特性

本节将讨论非线性系统的某些动态特性。一般的连续非线性系统的状态方程为

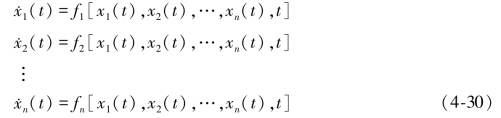
或写成向量形式,即̇x(t)=f[x(t),t],同样,非线性离散系统的状态方程的向量形式为x(k+1)=f[x(t),k]。在上面式子中,f是n维向量函数,x是n维状态向量。非线性特性给系统带来许多新的变化形式。例如,我们在本章一开始讲过,一个单一种群(如微生物)在世代之间如果有完全重叠的情况,则可用一阶常微分方程进行描述,即,其解(当初始值为N0时)为N=N0e rt,即N按指数规律增长,逐步趋向无穷大,但我们知道这是不可能的。由于环境容纳量(k)有限,所以增长方程为,而其解为,其中c是由初值条件决定的。这个式子表明,在开始时刻,当t较小时,N的变化近乎指数上升;当时间t趋于无穷大时,N趋于k。这个解所对应的曲线,便是著名的逻辑斯蒂曲线。从这个例子可以看出,描述客观事物单靠线性模型是不够的,而非线性关系的描述提供了更广泛的建模可能性。

严格地说,相当多的客观事物中各因素之间的关系都是非线性的,但在一定条件、一定范围内可以近似看成线性的。由于线性系统分析的方法比较成熟,因此许多问题都用线性模型来进行近似研究。但有些本质是非线性关系的,或者超出了线性范围的,就不能不从非线性的角度来进行分析了。可是到目前为止,非线性问题还没有像线性问题那样有通用的解法,当前还是只能就几类问题进行一些分析。另外,由于无法进行细节上的分析,研究常常仅限于一些关键性的性态,如稳定性、振荡(波动)等。

和线性模型一样,非线性模型的分析也着重研究平衡条件以及平衡点附近系统的性能。从状态方程可知,平衡点是代数方程组f(¯x,t)=0或(离散系统)¯x=f(¯x,k)的解。

2)相空间与相迹

由于直接求解非线性状态方程很困难,因此人们常常在状态空间中去研究系统运动时各状态变量间的关系,而不直接研究状态变量本身的变化。有时候,人们希望研究某一变量x及其各阶导数(̇x,¨x,…)之间的关系,便可在由x与其各阶导数构成的所谓的相空间中来分析问题。相空间可看作状态空间的一种特例,其中常用的是相平面,即由x与̇x构成的二维空间。

例如,有非线性动态方程

将上式改写成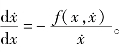在以x为横坐标、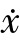为纵坐标的相平面上,相迹曲线是当时间t变化时,以t为参变量的̇x与x的函数关系曲线,而上面的表达式正是该曲线的斜率。

如果要想画出相迹曲线,可对式(4-31)直接积分求解,得出ẋ=F(x)的关系,即可画出,由于,两式相除,得曲线;也可以用图解法逐点寻求,因为相平面上任何一点(̇x,x)都对应相迹的一个斜率,按式(4-31)逐点计算便可连成相迹曲线。

下面研究一个非线性系统,其状态方程为

假定原点是它的平衡点,试研究原点附近系统的动态性能,我们试将上述两个方程在原点附近扩展成泰勒级数,即

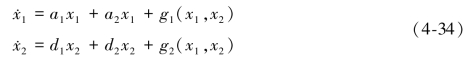
取线性近似,略去高阶项,得(www.zuozong.com)

令,两式合并,消去x2,得¨x+ḃx+cx=0,其中b=﹣a1﹣d1,c=a1d2﹣a2d1。其两个特征根为

当b、c参数不同时,λ1、λ2的值也不同,一般来说,它们可用复数形式表示。当它们的实部与虚部具有不同的数值与符号时,相迹也不同,图4-7画出了各种情况。

图中左边画的是A在复平面上的位置,右边是相应的相迹。由于相迹形状不同,所以平衡点的性质也不同,平衡点对应,该点称为奇点。

图4-7中还画出了特征根在复平面(σ,jω)上的位置。由于参数不同,特征根也不同,这样会产生6种情况。当特征根为一对具有负实部的复根时,系统动态特性具有衰减振荡特点,奇点为稳定焦点;当特征根为具有正实部的复根时,对应发散振荡,奇点为不稳定焦点;当特征根为一对负实根时,系统动态过程为非周期性衰减,奇点为稳定节点;当特征根为一对正实根时,对应非周期发散,奇点为不稳定节点;而当特征根为一对纯虚根时,对应持续振荡,奇点为中心点;如果特征根是一正一负两个实根,则动态过程或为衰减,或为发散,视初始条件而定,这时的奇点是鞍点。

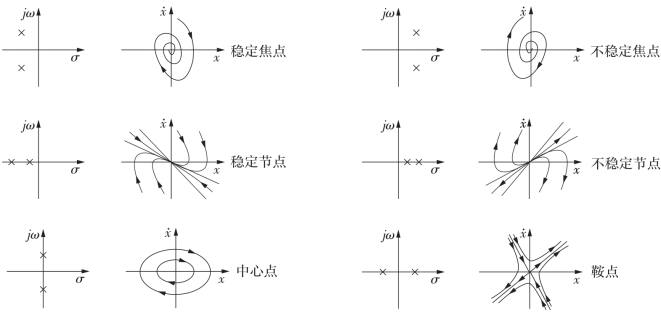
图4-7　特征根在复平面(σ,jω)上的位置

我们说过,系统参数变化,会引起特征根变化,因而动态过程特性也随之改变。图4-8画出了式(4-33)中不同b、c值下特征根与相迹的变化情况(图中

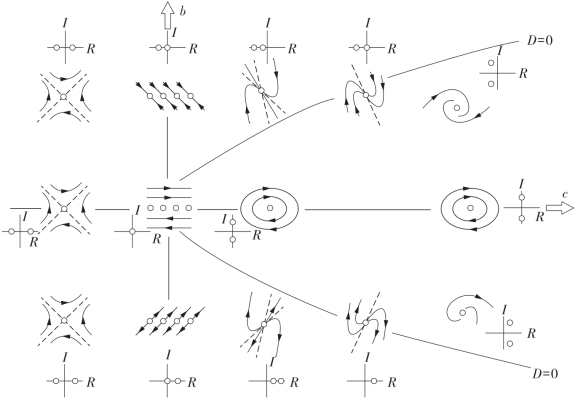
图4-8　不同b、c值下特征根与相迹的变化情况

非线性系统的相迹在形状上比线性系统更加多样化一些,但奇点与极限环也都存在,而多数极限环形状并没有规则。作为闭合曲线的极限环总是对应周期性运动,而在非线性系统的极限环中,又有稳定与不稳定两种。对稳定的极限环来说,当相迹(从内或从外)偏离它时,系统会自动地回到环上来,不稳定的极限环则在偏离后会远离它而趋向另一极限环或奇点。稳定的极限环对应稳定的持续振荡,它表明:依赖非线性能够维持稳定的振荡,否则会像线性情况那样,一旦某一参数发生变化,其动态过程特征也会变化。

例4-2　在由居民、企业组成的社会系统中,假设k表示人均持有资本量,其资本量随时间的动态方程可表示为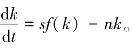其中,f(k)为企业采用资本进行生产的生产函数,且满足f′(k)≥0,f″(k)≤0;n表示人口增长率;s表示储蓄率。试用相图分析该系统的稳定性。

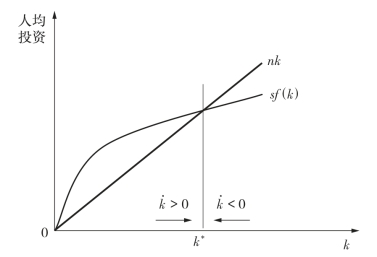
图4-9　人均持有资本量的相图

将图4-9中两条曲线的交点对应的资本存量记作k∗。当k=k∗时,实际投资恰好等于持平投资,即sf(k)=nk,从而̇k(t)=0,说明k=k∗时投资将保持不变。

在k=k∗处的左侧,即k<k∗时,sf(k)>nk,所以̇k>0,资本存量k将趋于增大;在k=k∗处的右侧,即k>k∗时,sf(k)<nk,所以̇k<0,资本存量k将趋于减小。上述分析表明,k=k∗是微分方程的稳定状态解。并且,无论起初的k值是否小于或大于k∗,都必然趋向k∗,一旦达到k∗,系统将处于全程稳定,资本存量不再变化。所以称k=k∗时,经济达到稳定状态,且称k∗为稳态资本存量。在经济达到稳定状态时,由方程sf(k∗)﹣nk∗=0可得该等式说明,一个系统的稳态资本存量最终取决于两个因素——人口增长率和储蓄率。当资本边际报酬大于时,k小于k∗,k将增大;资本边际报酬小于时,k大于k∗,k将减小。由于稳定状态路径上的资本存量不再变化,人均产出f(k∗)也将保持不变。这说明,稳定状态增长路径上的经济增长率等于0。