方程的建立：回归方程与相关系数之间的关系

一元线性回归分析是将因变量与自变量之间的关系用一个等式连接起来，构成一个数学表达式，即

式中：x 为自变量为因变量；a 是回归直线的起始值（截距），即x 为0 时的值，其数学意义为，在没有自变量的影响时，其他各种因素对因变量的平均影响；b 为直线斜率，这里又称回归系数。

这个表达式表示：自变量x每变动一个单位，因变量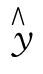平均变动b个单位。

通过a 和b 的取值，确定自变量与因变量的关系，a 和b 取不同的数值，就会得出不同的关系，即不同的直线。在这众多的直线中，我们总可以寻找出一条最能代表变量分布状态的、误差最小的直线。寻找误差最小的直线的方法，就是最小平方法，也是拟合直线最常用的方法。

最小平方法，又称最小二乘法，其原理是使原数列的实际观察值y 与预测值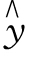的离差最小，数学表达式为：

将=a+ bx 代入上式中得到：

现在要解决的问题是，当a 和b 取什么值时，该式有最小值。这是一个二次方程式，求最小值的方法是求导数，且使导数等于0。

过程如下：

设Q=Σ（y-a-bx）2，为复合函数，要分别给a和b求导。

令Q'=（Σ（y-a-bx）2）'=0：

给a 求导结果为：

给b 求导结果为：

联立成方程组：

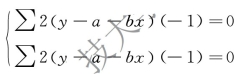
简化为：

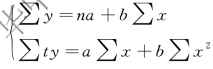
经过变形，又组成一个新的方程组：

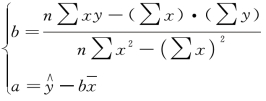
a、b 求出后，一元线性回归方程即可确定。

回归系数b 与相关系数r 之间还存在着如下的关系：

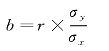(www.zuozong.com)

拟合直线方程的具体步骤如下：

首先，根据客观存在的变量，进行定性分析，判断变量之间有无内在联系。

其次，绘制散点图，做进一步的定性分析，判断变量之间相关关系的形态，观察其数量变化是否接近直线。

再次，如果接近直线，则进行定量分析，计算相关系数，只有根据相关系数得知变量之间呈现高度显著性线性相关或是显著性线性相关关系时，才有必要拟合一元线性回归方程，计算出参数，并确定方程。

最后，用方程预测变量变化趋势。

【例7-8】　表7-10是10 个企业生产性固定资产与利润增加额的数据，试根据表7-10 中的数据确定一元线性回归方程并预测当固定资产为1500 万元时，利润增加额可达到多少万元？

表7-10　10 个企业的相关资料　（单位：百万元）

解 （1）生产性固定资产与利润增加额有明显的相互联系。

（2）绘制散点图，如图7-6 所示。从数据点的走向来看，各数据趋势非常接近一条直线，可以拟合一条直线。

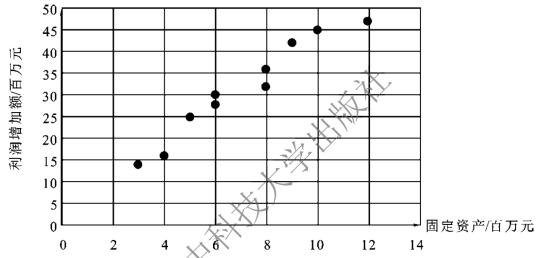
图7-6　固定资产与利润增加额散点图

（3）计算相关系数和一元线性回归方程参数，相关系数计算的相关参数计算过程如表7-11所示。

表7-11　相关系数计算的相关参数计算过程

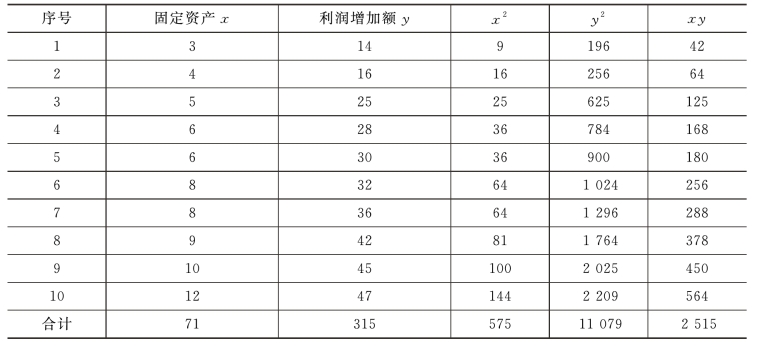
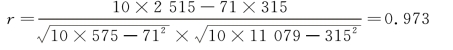
r=0.973，表明两个变量之间呈现高度显著性线性相关，可以进行一元线性回归分析。进一步计算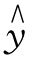=a+ bx 方程中的参数a 和b。依据公式计算如下：

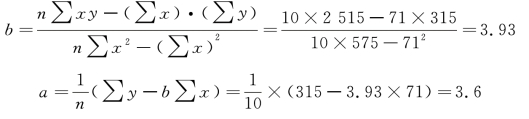
则一元线性回归方程为：

（4）用一元线性回归方程预测变量变化趋势。

将x=15 代入已知的回归方程，求出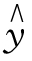的值即可：

即当固定资产为1500 万元时，利润增加额可达到6255 万元。

统计所研究的现象之间的相关关系，应该是真实的、客观存在的联系，而不是主观臆断或形式上的偶然与巧合，这就要求在实际进行相关关系分析时，依据有关的科学理论，通过观察和试验，在对现象做深入分析的基础上来确定这种联系，而且要经过理念和实践的进一步检验，只有这样，才能得到正确的结论。