拉普拉斯：天体力学和量热研究的先驱

拉普拉斯（1749—1827），法国著名物理学家、数学家和天文学家，天体力学的主要奠基人，天体演化学的创立者之一，分析概率论的创始人，应用数学的先驱．拉普拉斯用数学方法证明了行星的轨道大小有周期性变化．拉普拉斯曾任拿破仑的老师，在量热研究方面也有重大的贡献．图为拉普拉斯任职过的巴黎军事学院．

知能概述

物态变化时：熔化吸热Q＝m·λ（λ为熔化热）

汽化吸热Q＝m·L（L为汽化热）

物态不变时：Q吸＝cm（t-t0）

Q放＝cm（t0-t）

热平衡方程：两个物体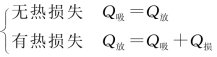

多个物体，在这多个物体组成的系统与外界无热交换时Q吸1＋Q吸2＋Q吸3＋…＋Q吸n＝0

问题解决

例1　洗澡时将11℃的冷水与66℃的热水充分混合成550kg、36℃的温水，在混合的过程中有2．31×106J的热量损失掉了，则所用冷水为________kg，所用热水为_________kg．

（上海市第二十二届初中物理竞赛大同中学杯复赛试题）

解题思路　此题属于典型的混合热量计算问题．解决思路是找质量关系：m混合＝m热＋m冷，找热量关系：Q放＝Q吸＋Q损，然后联立求解．

拉普拉斯冰量热器

把零摄氏度的冰做成一个中空的冰球，球内放入具有一定温度（高于零摄氏度）的物体，并尽量做到使整个装置与外界绝热．球内物体的温度会慢慢下降，球内壁的冰也慢慢熔化，直到球内物体的温度降到零摄氏度，物体的温度就达到稳定，球内的冰也不再熔化．这时只要测得熔化的水的质量，便可计算出物体从原来的温度降到零摄氏度所放出的热量，这个热量等于这些水由冰熔化时所吸收的热量．由物体的质量便可很容易地计算出它的比热容．

例2　如图所示，将质量为3kg的1200℃的铁块先后浸入两个盛有5kg水的开口容器中，容器中的水初始水温为25℃．不计容器壁吸收的热量．当第一个容器中的水温稳定后再将铁块浸入第二个容器中．则第一个容器中水的最后温度为_________；铁块的最后温度为_________．已知铁的比热容为0．5×103J／（kg·℃），水的比热容为4．2×103J／（kg·℃），大气压强恒为1个标准大气压．

例2图

（上海市第十七届初中物理竞赛大同中学杯复赛试题）

解题思路　物质混合后温度问题，可应用热平衡方程分析求解，但需注意水在1个标准大气压下的末温度只能为100℃．

例3　将50g、0℃的雪（可看成是冰水混合物）投入装有450g、40℃水的绝热容器中，发现水温下降5℃．那么在刚才已经降温的容器中再投入100g上述同样的雪，容器中的水温将又要下降（　）．

A．6℃　B．7．5℃　C．9℃　D．10℃

（上海市第二十届初中物理竞赛大同中学杯初赛试题）

解题思路　先用热平衡方程求出50g、0℃的雪融化为0℃的水所需吸收的热量，再用热平衡方程求投入100g同样的雪后，容器中的水降低的温度．注意第2次投放雪时，水的质量已变为了500g．

例4　人的体温是由“下丘脑”中特殊神经细胞组织控制的，它对人体体温的变化很敏感，当下丘脑温度高于37℃时，人体散热机制（如血管舒张、出汗等）就会活跃起来．已知37℃时蒸发18g汗水所需要的能量为4300J．现有一中年人漫步行走时，每秒钟体内产生的热量为35J，而此时人体通过传导、辐射等方式（不包括出汗）产生的散热功率只有33W，因此还要通过出汗的方式才能保持37℃的体温不变．那么此人漫步行走1h出汗约（　）．

A．20g　B．30g　C．40g　D．50g

（上海市第十九届初中物理竞赛大同中学杯初赛试题）

解题思路　人行走时产生热量的功率为35W，通过传导、辐射等方式的散热功率只有33W，还有2W的散热功率需要通过排汗来解决．

计算1h需要通过排汗散发的热量和汗水的蒸发热即可求出汗水的质量．

热量：人类生命的原料

维持人类生命的原料是我们吃进去的食物．这些食物到达体内后，经过化学作用，使其中所含的蛋白质、脂肪、碳水化合物发出热量，作为动力来供给人体内外的各种活动．离开了食物，人类就不能生存．维持体内的各种活动如血液的循环、心脏的跳动、胃肠的消化和排泄等都需要食物供给的热量．体外活动的方式虽然不同，但都需要热量作动力．不过劳动的强度不同，所需的热量也不相同．劳动强度越大，消耗的热量也越多．

多物体混合的热量计算

例5　已知冰的比热容为2．1×103J／（kg·℃），冰的熔化热为3．36×105J／kg，水的比热容为4．2×103J／（kg·℃）．把质量为10g、温度为0℃的冰和质量为200g、温度为100℃的金属块同时投入质量为100g、温度为20℃的水中，当它们达到热平衡时，它们的共同温度为30℃．若不计热量损失，求金属块的比热容．

（上海市第八届初中物理竞赛普陀杯复赛试题）

解题思路　此题属于多物体混合问题，当它们与外界没有热交换时，它们吸热的总和为零．即Q冰熔化＋Q冰水吸＋Q水吸＋Q金属吸＝0．

热平衡方程组的联立计算

例6　温度不同的两个物体相互接触后将会发生热传递现象．若不计热量的损失，则当两物体达到热平衡状态时，它们的温度相同，且高温物体放出的热量等于低温物体所吸收的热量．现有三种不同的液体A、B、C，它们的初温度分别为15℃、25℃、35℃．当A和B液体混合并达到平衡状态时，其平衡温度为21℃；当B和C液体混合并达到平衡状态时，其平衡温度为32℃．求A和C液体混合并达到平衡状态时的平衡温度．

（上海市第五届初中物理竞赛复赛试题）

解题思路　本题属于多物体间的两两平衡问题．每两个物体的平衡都有一个平衡方程，先将各平衡方程列出，再联立求解．

1．有甲、乙两个物体，已知甲物体的比热容是乙物体的2倍，甲物体的质量是乙物体的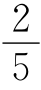．若它们吸收相同的热量，则它们升高的温度之比为Δt甲∶Δt乙＝________．

（上海市第五届初中物理竞赛复赛试题）

2．北方的冬天天气比较寒冷，房间内一般都要安装暖气片供暖．在房间暖气片温度保持不变的情况下，房间内的平衡温度将随外界温度的变化而变化．研究表明，房间内暖气片和房内的温差与房间内外的温差之比保持不变．当外界温度为-23℃时，房间内的温度长时间保持13℃不变；当外界温度为-18℃时，房间内温度长时间保持16℃不变，则房间内暖气片的温度应为________℃．当房间内温度长时间保持25℃不变时，外界温度为________℃．

（上海市第十八届初中物理竞赛大同中学杯初赛试题）

成年人每日每公斤体重约需的热量

工作种类　约需热量（单位：kcal）

休息　0～35

轻体力劳动　35～40

中等体力劳动　40～45

重体力劳动　45～50

极重体力劳动　50～70

轻体力劳动指售货、讲课等，中等体力劳动指学生的日常活动、机动车的驾驶等，重体力劳动指非机械化农业劳动、体育运动等，极重体力劳动指伐木、采矿等．

3．甲、乙两液体的密度比为ρ甲∶ρ乙＝5∶4，体积比为V甲∶V乙＝2∶3，比热容比为c甲∶c乙＝1∶2，且它们的初温不等．现将它们混合（不发生化学反应），不计混合过程中的热损失，达到热平衡后液体温度相对各自初温变化量的绝对值分别为Δt甲和Δt乙，则Δt甲∶Δt乙为（　）．

A．16∶15　B．15∶16　C．12∶5　D．5∶12

（上海市第二十九届初中物理竞赛大同中学杯初赛试题）

4．将一杯热水倒入容器内的冷水中，冷水温度升高10℃，又向容器内倒入同样一杯热水，冷水温度又升高6℃，若再向容器内倒入同样一杯热水，则冷水温度将再升高（不计热损失）（　）．

A．5℃　B．4℃　C．3℃　D．2℃

（上海市第二十七届初中物理竞赛大同中学杯初赛试题）

5．A、B两物体质量相等，温度均为10℃，甲、乙两杯水质量相等，温度均为50℃，现将A放入甲杯，B放入乙杯，热平衡后，甲杯水温降低了4℃，乙杯水温降低了8℃，则A、B两种物质的比热容之比为（　）．

A．2∶3　B．3∶5　C．4∶9　D．1∶2

（上海市第二十二届初中物理竞赛大同中学杯初赛试题）

6．著名物理学家费米根据侦探小说的内容得知，一具尸体大约需要半天时间才能从体温37℃降至室温25℃．另外他通过实验室提供的数据还了解到：体重约60kg的正常人的比热（容）与水相当，约为4200J／（kg·℃），每千克葡萄糖完全分解释放的热量为1．6×107J，此外，尸体的散热量大约为正常人在相同时间内散热量的60%．根据这些数据估算出一个正常人体内每天必须补充的葡萄糖为（　）．

A．630g　B．63g　C．840g　D．84g

（上海市第十七届初中物理竞赛大同中学杯初赛试题）

7．质量相等的28℃、100℃的水分别装在甲、乙两容器中，现将一个温度为100℃的金属球放入甲容器中，达到温度相同时，甲容器中水温升高到40℃，然后迅速取出金属球放入乙容器中，再次达到温度相同时，乙容器中水温是（设不计热量损失和水的质量损失）（　）．

A．60℃　B．70℃　C．88℃　D．90℃

（上海市第十三届初中物理竞赛太奇杯复赛试题）

8．甲、乙两容器中装有质量相等的水，水温分别为25℃和75℃，现将一温度为65℃的金属球放入甲容器中，热平衡后水温升高到45℃，然后迅速取出金属球并放入乙容器中，热平衡后乙容器中水温为（不计热量散失和水的质量的变化）（　）．

A．65℃　B．60℃　C．55℃　D．50℃

（上海市第二十六届初中物理竞赛大同中学杯初赛试题）

9．在相同的加热条件下，对质量为m1、比热容为c1的物质A和质量为m2、比热容为c2的物质B均匀加热，物质A、B的温度随加热时间的变化情况如图所示．根据图象分析可推断出正确的结论是（　）．

A．若c1＝c2，则m1＜m2

B．若c1＞c2，则m1＞m2

C．若m1＝m2，则c1＜c2

D．若m1＜m2，则c1＞c2

第9题图

（上海市第十三届初中物理竞赛太奇杯初赛试题）

10．在27℃的室温下，将20℃的1kg水与15℃的2kg水混合，由于实验装置不够精密，在混合过程中与周围物体有8．4×103J的热量交换，则混合后水的温度为（　）．

A．16．7℃　B．17．3℃　C．18．3℃　D．20．0℃

（上海市第十三届初中物理竞赛太奇杯初赛试题）

11．把加热到100℃的某铁块投入m1克20℃的水中，混合温度为40℃；把加热到100℃的该铁块投入m2克20℃的水中，混合温度为60℃；如果把同样加热到100℃的该铁块投入（m1＋m2）克20℃的水中，混合温度为（　）．

A．50℃　B．48℃　C．36℃　D．32℃

（上海市第十二届初中物理竞赛初赛试题）

12．两种不同的液体，它们的质量、比热容、初温度分别为m1和m2、c1和c2、t1和t2，且t2＞t1．若不计热量损失，则把它们混合后的共同温度为（　）．

（上海市第八届初中物理竞赛普陀杯初赛试题）

13．在两个相同的杯子内盛有质量相等的热水和冷水，将一半热水倒入冷水杯内，冷水杯内的温度升高21℃，若再将热水杯内剩余热水的一半倒入冷水杯内，冷水杯内的水温会升高（　）．

A．9℃　B．8℃

C．6℃　D．5℃

（上海市第三十一届初中物理竞赛初赛试题）

14．如图所示，在一大块温度为0℃的平整的冰上有一个体积为V0＝1000cm3的洞，用带小孔的不导热泡沫塑料板覆盖在冰面上．现从小孔向洞内缓慢注入温度为100℃的水，为不让水从小孔中溢出，至多能注入多少千克100℃的水？（已知冰的密度ρ冰＝0．9×103kg／m3，冰的熔化热λ＝334kJ／kg）

第14题图

（上海市第三十届初中物理竞赛复赛试题）

15．小明拿了一只有温度显示的保温电热水瓶．装上一定量的水之后，温度计的示数为T0＝20℃．经过t1＝1min，水被加热到T1＝40℃，他往电热水瓶里又注入了一些水，在t2＝3．5min的时刻，水的温度达到了T2＝50℃．小明不再往电热水瓶里注水了．又过了5min水烧开了．如图所示为热水瓶里水的温度在加热和注水的过程中的变化图象．试求：注入的水的温度Tx等于多少？

第15题图

（上海市第三十届初中物理竞赛复赛试题）

16．质量相等的A和B两固体，它们的初温度均为20℃．把A和B同时放入盛有沸水的大锅炉内后，它们分别以每克每秒12．6J和每克每秒42J的吸热速度吸收热量．A和B的比热容分别为2．1×103J／（kg·℃）和3．36×103J／（kg·℃），且在吸热过程中，A和B两个物体均未发生物态变化，求10s内：

（1）A物体的温度和它每克吸收的热量．

（2）B物体的温度和它每克吸收的热量．

（上海市第七届初中物理竞赛风华杯复赛试题）

17．将一勺热水倒入盛有一些冷水的保温容器内，使得冷水温度升高5℃．然后又向保温容器内倒入同样一勺热水，水的温度又上升了3℃．如果再连续倒入10勺同样的热水，则保温容器内的水温度还会升高多少摄氏度（保温容器吸收热量忽略不计）？

（上海市第十二届初中物理竞赛复赛试题）

18．小明看到一句农谚：“下雪不冷化雪冷．”他很好奇，想具体了解一下冰雪熔化时究竟要吸收多少热量．于是查找了资料，知道“熔化热”的定义是：单位质量的某种晶体，在熔化成同温度的液体时吸收的热量，叫作这种晶体的熔化热．他想用实验测量一下冰的熔化热，于是找来了一些实验器材：一架天平和配套的砝码、一支实验室用温度计（0℃～100℃）、一个有密封盖子的保温桶、一个小烧杯、一把镊子和一个专门用来在冰箱中冻小冰块的塑料冰格，又观察到家里的冰箱面板上显示冷冻室温恒为-18℃．请帮助小明设计一个用这些器材粗测冰块熔化热的方案，要求写出实验的步骤和用测量的物理量计算冰的熔化热λ的表达式（水和冰的比热容分别用c水和c冰表示）．

（第二十二届全国初中应用物理知识竞赛复赛试题）

19．有六个完全相同的杯子，其中一个盛满热水，如果要利用杯子的吸热作用把热水的温度降低，可以把热水注入其余的五个冷杯子中，让杯子吸收热水的热量，怎样注入热水可以获得最佳的冷却效果？

［方法一］把热水平均注入五个杯子中，每个杯子分配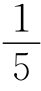热水．

［方法二］先把热水整杯注入第二个杯子，等杯子不再吸热时，再整杯注入第三个杯子，如此类推，最后注入第六个杯子．

（1）你选择哪个方法？写出选择理由．

（2）如果热水质量是100g，温度是90℃，玻璃杯质量是50g，温度是10℃，玻璃的比热容为0．84×103J／（kg·℃），请计算能使热水降到的最低温度．

（第四届英才杯初中物理应用知识竞赛试题）(www.zuozong.com)

例1　290；260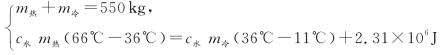

例2　100℃；30℃　先放入第一个容器，

Q放＝c铁m铁Δt＝0．5×103×3×（1200-100）J＝1．65×106J

Q水吸＝c水m水Δt′＝4．2×103×5×（100-25）J＝1．575×106J

因为Q放＞Q水吸，所以水吸热沸腾后，稳定温度为100℃．

再放入第二个容器，c铁m铁（100℃-t共）＝c水m水（t共-25℃），解之t＝30℃

例3　B　先计算450g水温度降低5℃所放出的热量：Q放＝cmΔt＝c×450×5＝2250c

再计算50g 0℃的水温度升高到35℃所吸收的热量：Q水＝cmΔt＝c×50×35＝1750c

两者差值为500c，表示每50g 0℃的雪转化为0℃的水需要吸收500c的热量（熔化热）．

利用热平衡方程计算第二次热传递（设水温将再降低Δt，则最终水温为35℃-Δt）：

c×100×（35-Δt）＋2×500c＝c×500×Δt，解此方程可得Δt＝7．5（℃）

例4　B　P排汗＝35W-33W＝2W，1h通过排汗散发的热量W＝P·t＝2×3600＝7200（J）

m汗＝×18g≈30g

例5　Q冰熔化＋Q冰水吸＋Q水吸＋Q金属吸＝0

m冰λ＋m水c水（t-0℃）＋m水c水（t-t水初）＋c金m金（t-t金初）＝0

10g×3．36×102J／g＋10g×4．2J／（g·℃）×（30℃-0℃）＋100g×4．2J／（g·℃）×（30℃-20℃）＋c金×200g×（30℃-100℃）＝0

解之c金＝0．63×103J／（kg·℃）

例6　A、B混合　cAmA（21℃-15℃）＝cBmB（25℃-21℃）……①

C、B混合　cCmC（35℃-32℃）＝cBmB（32℃-25℃）……②

A、C混合　cAmA（t-15℃）＝cCmC（35℃-t）……③

①÷②有代入③式t＝30．6℃

1．5∶4

2．67；-3　根据题目给出的条件，可以列出比例式（设暖气片的温度为t0，所求的外界温度为t1）：

3．C

4．B　设一杯热水的质量为m热，初温度为t热，第一次的混合温度为t共1，冷水质量为m冷．

第一次倒入：有m热·c·（t热-t共1）＝m冷·c×10℃……①

第二次倒入：有m热·c·［t热-（t共1＋6℃）］＝（m冷＋m热）·c×6℃……②

第三次倒入：有m热·c·［t热-（t共1＋6℃＋Δt）］＝（m冷＋2 m热）·c·Δt……③

①-②：m热×6＝m冷×4-m热×6，则m冷＝3 m热

③式可分解为m热［t热-（t共1＋6℃）］-m热·Δt＝（m冷＋2 m热）·Δt……④

②式与④式联立，解之Δt＝4℃

5．C mA＝mB m甲＝m乙

A放入甲杯：cAmA（46℃-10℃）＝c水m甲×4℃

B放入乙杯：cBmB（42℃-10℃）＝c水m乙×8℃

解之

6．A　依题意Q放＝Q散，即λm1＝2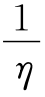·cm2Δt

7．D　在甲容器中平衡时，c金m金（100℃-40℃）＝c水m水（40℃-28℃）……①

在乙容器中平衡时，c金m金（t-40℃）＝c水m水（100℃-t）……②

①式与②式两边分别相除得，解之t＝90℃

8．B　①当将金属球放入甲容器中时，金属球放出的热量与水吸收的热量相等，即Q金＝Q水．

设金属球的质量为m金，比热容为c金，水的质量为m水，水的比热容为c水．

则Q金＝m金×c金（65℃-45℃），Q水＝m水×c水（45℃-25℃）

因为Q金＝Q水，所以m金×c金（65℃-45℃）＝m水×c水（45℃-25℃）

化简得

②当将金属球放入乙容器中时，乙容器中的水放出的热量与金属球吸收的热量相等，即Q′水＝Q′金．

由于甲、乙容器中的水的质量相等，又是同一个金属球，所以仍设金属球的质量为m金，比热容为c金，水的质量为m水，水的比热容为c水，此时两者共同的温度为t．

则Q′水＝m水×c水（75℃-t），Q′金＝m金×c金（t-45℃）

因为Q′水＝Q′金，即m水×c水（75℃-t）＝m金×c金（t-45℃），所以75℃-t＝t-45℃

解得t＝60℃

9．D　相同的加热条件指在相同的时间内吸热相等，取相同时间，如答图QA＝QB，Δt2＞Δt1，c1m1Δt1＝c2m2Δt2

若c1＝c2，则m2＜m1

若m1＝m2，则c2＜c1

若m1＜m2，则c1一定大于c2．

10．B　c水m水（t-20℃）＋c水m′水（t-15℃）＝8．4×103J

4．2×103J／（kg·℃）×1kg×（t-20℃）＋4．2×103J／（kg·℃）×2kg×（t-15℃）＝8．4×103J

解之t＝17．3℃

11．C　c铁m铁（100℃-40℃）＝c水m水1（40℃-20℃）……①

c铁m铁（100℃-60℃）＝c水m水2（60℃-20℃）……②

①÷20＋②÷40有3c铁·m铁＋c铁·m铁＝c水·（m水1＋m水2）……③

c铁m铁（100℃-t）＝c水（m水1＋m水2）·（t-20℃）……④

第9题答图

③÷④有，解之t＝36℃

12．B

13．C　设原来热水和冷水的温度分别为th、tc，t1-tc＝21℃，当一半热水倒入冷水杯内后：

c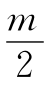（th-t1）＝cm（t1-tc），所以th-t1＝2（t1-tc）＝42℃，th＝tc＋63℃

当再将热水杯内剩余热水的一半倒入冷水杯内后：

th-t2＝6（t2-t1）

tc＋63℃-t2＝6（t2-tc-21℃）

所以t2＝tc＋27℃，因此冷水杯内的水再次升高的温度为t2-t1＝6℃．

14．100℃的水降温到0℃放出的热量将被冰吸收使冰熔化，

有cm水Δt＝λm冰

4．2×103J／（kg·℃）×m水×100℃＝334×103J／kg×m冰

水的体积＋熔化了的冰变成的水的体积＝洞的体积＋熔化了的冰的体积

即

代入数据，可得m水＝1．162kg

15．由图表的斜率可得：开始时的加热速度为20℃／min，最后水的加热速度为10℃／min，可见加入的水的质量和加入前水的质量相同，均设为m．如果加入的水也是40℃，那么3．5min的时刻，根据质量加倍，加热速度减半为10℃／min，从1～3．5min，经过了2．5min，10×2．5＝25（℃），水温应升高为65℃，而实际只有50℃，所以少升高15℃的原因是：使2 m质量的水升高15℃的热量消耗在了使加入的m质量的水温度从Tx升高到40℃的过程中，即2 m×15℃＝m×Δt

Δt＝30℃

Δt＝40℃-Tx

Tx＝10℃

16．（1）对于A物体，若10s内都在吸收热量，Q吸A＝mA×10×12．6＝126 mA

126 mA＝cAmA（t-20℃）

126 mA＝2．1×mA（t-20℃），解之t＝80℃

所以每克A物体吸热126J，末温为80℃．

（2）对于B物体，若Q吸B＝mB×10×42＝420 mB

420 mB＝cBmB（t-20℃），解之t＝145℃

由于B物体的最终温度不能超过100℃，故B物体没有吸收10s的热量，每克B物体吸热

Q＝1g×3．36J／（g·℃）×（100℃-20℃）＝268．8J，末温为100℃．

17．第一勺热水倒入：c水m热［t热初-（t冷初＋5℃）］＝c水m冷·5℃

第二勺热水倒入：c水m热［t热初-（t冷初＋8℃）］＝c水（m冷＋m热）·3℃

联立解之m冷＝3 m热，t热初-t冷初＝20℃

将总共12勺热水倒入冷水中，设冷水温度升高Δt，有

12c水m热［t热初-（t冷初＋Δt）］＋c水m冷［t冷初-（t冷初＋Δt）］＝0

解之Δt＝16℃，后10勺热水倒入后升高的温度为16℃-8℃＝8℃

18．实验步骤：

（1）用调好的天平测量小烧杯的质量m1；

（2）用小烧杯盛取足量的水，再用天平测量小烧杯和水的质量m2；

（3）将水倒入保温桶内，用温度计测量水的温度t1；

（4）提前较长时间用冰格盛适量水放在冰箱冷冻室里冻成冰块，用镊子取适量冰块放在小烧杯中，迅速用天平测量出其总质量m3后，立刻将冰块倒入保温桶内的水中，盖紧桶盖；

（5）轻轻摇晃保温桶使水温均匀，并仔细听声音，听出冰块熔化完毕后，打开桶盖，用温度计测出保温桶内水的温度t2．

冰块的熔化热的表达式为：λ＝

19．（1）应该选择方法二．因为方法二中前几个杯子倒入热水后，杯子升高的温度都会比方法一中杯子升高的温度高，表明吸收的热量比第一种方法多，所以热水降温多，故应选择方法二．

（2）方法二中，第一个杯子升高到的温度

同理t2＝76．1℃　t3＝70．1℃　t4＝64．6℃　t5＝59．7℃

所以能使热水降低到的最低温度是59．7℃．