【摘要】:一、选择题(本大题共12小题,每小题3分,共36分)二、填空题(本大题共6小题,每小题3分,共18分)13.x≥-314.415.x=-116.1.1a17.18.6三、解答题(本大题共7小题,共46分)19.220.化简得:,代入得:21.证明:∵四边形ABCD是正方形,∴AB=BC=DC,∠ABC=∠BCD=90°.∵E是边AB的中点,F是边BC的中点,∴BE=AB,CF=BC,∴BE

一、选择题(本大题共12小题,每小题3分,共36分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.x≥-3 14.4 15.x=-1
16.1.1a 17.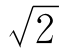 18.6
18.6
三、解答题(本大题共7小题,共46分)
19.2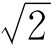
20.化简得:![]() ,代入得:
,代入得:![]()
21.证明:∵四边形ABCD是正方形,
∴AB=BC=DC,
∠ABC=∠BCD=90°.
∵E是边AB的中点,F是边BC的中点,
∴BE=![]() AB,CF=
AB,CF=![]() BC,
BC,
∴BE=CF.
在△BCE与△CDF中: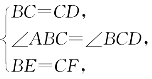
∴△BCE≌△CDF,
∴CE=DF.
22.(1)12÷25%=48(人).
(2)连线如下图所示:
(3)P(参加的比赛项目相同)=![]()
23.解:过点P作PC⊥AB,垂足为C,
设PC长为xkm.
∵点P在工厂B北偏西45°方向上,
∴∠PCB=45°,
∴BC=PC=x.(www.zuozong.com)
∵点P在工厂A北偏东60°,
∵AB=3km.
∴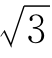 x+x=3,
x+x=3,
解得:x≈1.05<1.2,
答:修筑公路时,这个村庄有居民需要搬迁.
24.(1)由勾股定理可得:AC=![]() =4.
=4.
(2)证明:连接OC.
∵AC是∠DAB的平分线,
∴∠CAD=∠CAB.
∵OA=OC,
∴∠OCA=∠CAB,
∴∠OCA=∠CAD,
∴OC∥AD.
∵AD⊥CD,
∴OC⊥CD.
∵点C在圆周上,
∴直线CD是⊙O的切线.
25.解:(1)由待定系数法可求得函数解析式为y=x2-2x-3.
(2)当点P到点A、点B的距离之和最短时,点P是对称轴与x轴的交点.
直线l=-![]() =1,
=1,
∴点P的坐标为(1,0).
(3)(1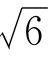 ),(1,-
),(1,-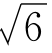 ),(1,0)
),(1,0)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




