统计学中的相关系数及计算方法

1.相关系数的概念

相关图、相关表可以帮助我们直观地看出所研究的变量之间是否存在相关关系,以及所呈现出的相关关系形式,但是不能确切地表明相关关系的密切程度。当两个变量存在直线相关时,我们一般借助相关系数这一指标说明其相关的密切程度。

什么是相关系数? 它是研究和判断两个变量之间直线相关关系密切程度和方向的统计指标,一般用r 表示。相关系数具有以下几个特点和性质:

(1)相关系数的大小只能判断两个变量之间是否有直线相关关系及其密切程度和方向,而不能作为曲线相关关系的判断依据。例如,当相关系数很小甚至为零时,只能说变量之间不存在直线相关而不能说它们不存在相关关系。曲线相关关系的密切程度判断方法是计算相关指数指标。

(2)测定相关关系时是无需分辨自变量和因变量的,所以两个变量之间如果存在直线相关关系,则计算的相关系数只有一个。

(3)相关系数的计算,要求两个变量的数据都是随机抽选的。即在选择计算相关系数所需的统计资料时,所有数据不能凭选用者主观愿望来确定,这样才能保证计算结果的客观、准确。

(4)相关系数有正负之分。当相关系数为正值时,说明两个变量之间存在着正相关关系;相反,相关系数为负值时,说明两个变量之间存在着负相关关系。

(5)相关系数取值范围为|r|≤1。|r|愈接近1,说明两个变量之间的直线相关关系密切程度就愈高;愈接近0,则直线相关关系的密切程度就愈低。在实际应用中,利用相关系数判断直线相关关系的密切程度的一般标准:

当|r|=0时,说明两个变量之间不存在直线相关关系;

当0<|r|≤0.3时,认为两个变量微弱直线相关;

当0.3<|r|≤0.5时,认为两个变量低度直线相关;

当0.5<|r|≤0.8时,认为两个变量显著直线相关;

当0.8<|r|<1时,认为两个变量高度直线相关;

当|r|=1时,说明两个变量之间存在完全直线相关关系,即成直线函数关系。

2.相关系数的计算

(1)相关系数基本公式

式中:

σx 为自变量x 的标准差,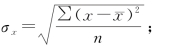

σy 为因变量y 的标准差,

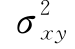为x 与y 的协方差,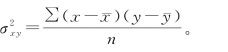(www.zuozong.com)

所以,相关系数的计算公式也可写成:

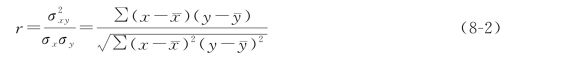
(2)相关系数的简捷计算公式

根据基本公式计算比较烦琐,实际中通常采用下列简捷公式来计算相关系数:

1)根据未分组资料计算

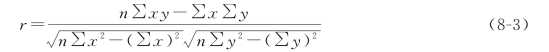
【例8.1】根据案例导入提供的资料计算生产费用与产量之间的相关系数,说明两个变量之间相关的密切程度。

解:计算相关系数时,两个变量都是随机变量,不需区分自变量和因变量。为了方便计算,这里设产量为自变量 (x),生产费用为因变量 (y),有关数据计算见表8-4。

表8-4　生产费用与产量相关系数计算表

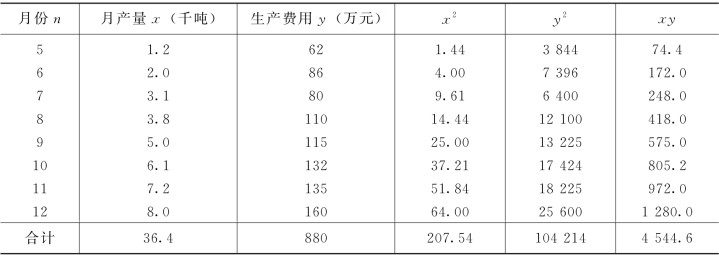
根据表中数据可知:

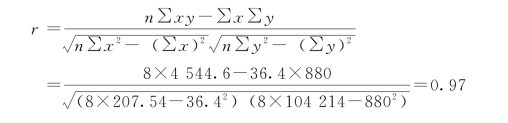
r=0.97说明生产费用与产量之间存在高度正直线性相关关系。

2)根据单变量分组资料计算

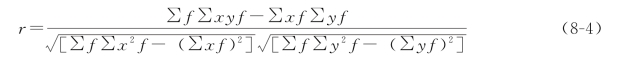
【例8.2】为了研究家庭收入与家庭消费支出关系,通过抽样调查获得40个家庭的月收入与月消费支出的资料,先整理成分组相关表,如表8-5所示。以各组家庭月收入为x,家庭个数为权数f,各组家庭月平均支出为y,列计算表如表8-5所示。

表8-5　家庭收入与家庭消费支出相关系数计算表

将表中计算数据代入公式得:

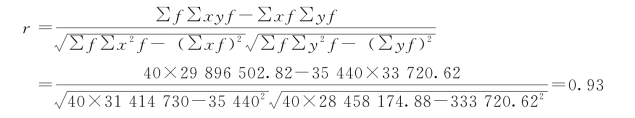
说明家庭月收入和家庭月支出高度正线性相关。