整体性分析高中数学教师TPACK知识水平

1.研究样本信息

通过电子版和纸质版问卷的收集和统计，最终回收问卷195份，有效问卷188份，有效率为96.4%，有效问卷被试的基本信息如表6.2。

表6.2　被试的基本信息

2.高中数学教师TPACK知识水平的整体性分析

运用SPSS 22.0测试教师TPACK各维度的整体水平，计算7个维度知识的均值、标准差、方差。

表6.3　TPACK整体比较

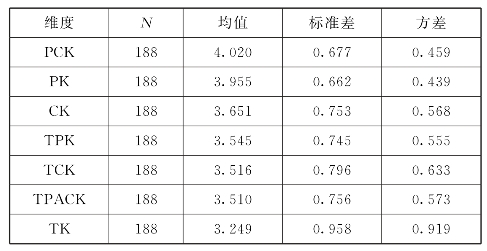
根据表6.3中数据可得，TPACK各维度的均值排序为PCK＞PK＞CK＞TPK＞TCK＞TPCK＞TK。并且通过计算，TPACK 7个维度的组成元素得分均值为3.65，我国初中数学教师在平面图形变换的TPACK知识水平处于中等偏上。PCK、PK以及CK均值得分大于整体均值，另外的4个维度TPK、TCK、TPACK以及TK均值得分小于整体均值。PCK得分最高，平面图形变换的教学知识水平最高。TK得分最低，技术知识掌握是最差的，并且标准差和方差最大。

表6.3数据显示，初中数学教师在平面图形变换的教学中，对学科教学知识、教学法知识和学科内容知识的运用有自信心，掌握能力强。在没有信息技术的支持下，初中数学教师能够很好地掌握平面图形变换的基础知识，进行平面图形变换的教学，做好教学管理工作，有信心并且能够做好平面图形变换的教学工作。在没有引入信息技术时，PCK得分高于PK、CK得分。在引入信息技术进行辅助教学时，对于信息技术的使用、将信息技术与教学知识和学科知识相融合存在问题。这些问题的根本原因在于信息技术掌握能力弱。

3.核心元素知识的比较分析

TK、CK和PK是组成教师TPACK知识的要素，也是其他复合知识的基础。对核心元素知识TK、CK和PK进行单个样本t检验，结果如表6.4所示。

表6.4　核心元素知识单个样本检验

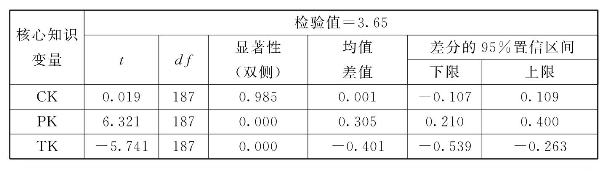
由表6.4可知，初中数学教师对教学知识的掌握明显优于对平面图形变换知识和技术知识的掌握，技术知识分值过低，初中数学教师信息技术能力水平很低。

4.复合元素知识的比较分析

复合知识是核心元素知识融合生成的新知识。教师TPACK复合知识包括PCK、TCK、TPK、TPACK。用SPSS 22.0对复合知识进行单样本t检验，结果如表6.5所示。

表6.5　复合元素知识单个样本检验

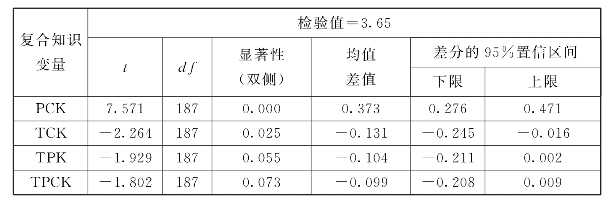
由表6.5可知，其中PCK与其他三种复合知识差距很大，但这三种复合知识分值差不多。说明初中数学教师在平面图形变换的教学中，学科教学能力强，在没有信息技术的条件下，能够很好地胜任平面图形变换的教学工作。初中数学教师将信息技术与教学整合的能力强于将信息技术与平面图形变换知识整合的能力。

5.CK（学科内容知识）发展差异分析

（1）CK各题平均分差异分析

CK（学科内容知识）是整合教师的学科教学知识的基本要素之一，是教师进行教学传授的内容。图6.1为初中数学知识平面图形变换的CK知识的得分情况。

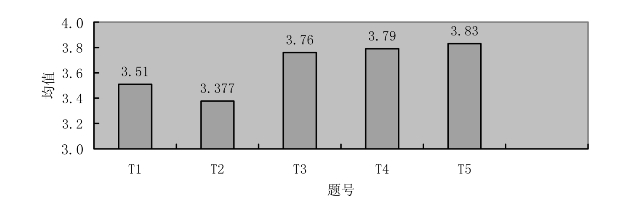
图6.1　CK测试题平均得分

这几道题分别是对平面图形变换的基础知识、拓展知识、数学思想、数学应用以及阶段作用的测试。明显可以看出，初中数学教师在后3个方面分值较高，抓住了其中的数学思想，对平面图形变换的整体作用有良好的把握。基础知识、拓展知识分数分别为3.51、3.377。说明初中数学教师更多的是拘泥于书本上的知识，拓展知识能力需要加强。

（2）CK性别差异分析

下面对初中数学教师CK（学科内容知识）在性别方面的差异进行分析。需进行独立样本t检验，结果如表6.6所示。

表6.6　CK性别差异分析

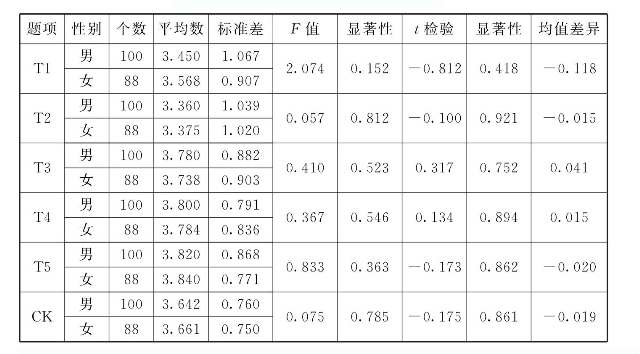
注：*p＜0.05，均值在0.05水平上有显著差异。T1：基础知识，T2：拓展知识，T3：地位和作用的认识，T4：数学思想，T5：实际处理。

对各题男女平均分进行比较，在T1：基础知识，T2：拓展知识，T5：实际处理，女性高于男性。而在T3：地位和作用的认识，T4：数学思想两题上，男性明显高于女性。男性CK得分为3.642，女性CK得分为3.661，男性高于女性。经过双重t检验，t值等于－0.175，p＝0.861＞0.05，说明初中数学教师CK在性别上没有显著差异。并且初中数学教师在CK其他各题目也没有明显的性别差异。

（3）CK教龄差异分析

将教龄分为：0～5年（A）、6～10年（B）、11～15年（C）以及16年及以上（D），为连续变量，采用单因子方差分析ANOVA，进行方差齐性检验（若满足方程齐性检验进行多重比较，否则使用Dunnett T3检验）。Levene3统计量F＝1.27，p＝0.285＞0.05，未达到显著。对初中数学教师在CK（学科内容知识）在教龄方面的差异进行分析。结果如表6.7所示。

表6.7　CK教龄差异分析表

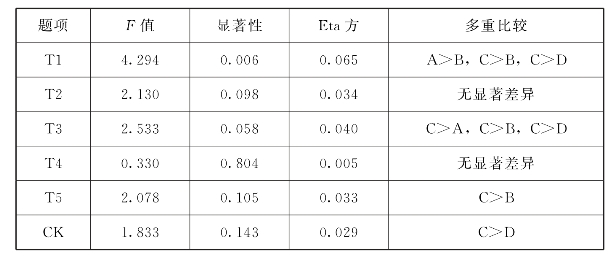
表6.7显示，CK教龄差异检验的F＝1.833，p＝0.143＞0.05，未达到显著性水平，Eta方为0.029，初中数学教师CK与教师年龄的关联度为2.9%，关联程度低。通过各题目的LSD多重比较分析看出，教龄在11～15年（C）教师比教龄在16年及以上（D）教师有更好的学科内容知识，但差异不明显。在基础知识上，F＝4.294，p＝0.006＜0.05，达到显著水平，教龄为0～5年（A）的教师比教龄为6～10年（B）教师基础知识更牢固，教龄为11～15年（C）教师比教龄为6～10年（B）和16年及以上（D）教师基础知识更牢固。在地位和作用的认识上，F＝2.533，p＝0.058，教龄为11～15年（C）教师均比教龄为0～5年（A）、6～10年（B）和16年及以上（D）教师认识更清晰，但差异没有太明显。在实际问题处理上，F＝2.078，p＝0.105，教龄为11～15年（C）的教师比教龄为6～10年（B）的教师处理问题能力更强，但差异不明显。

（4）CK职称差异分析

将教师职称分为：中教三级（A）、中教二级（B）、中教一级（C）以及高级（D），采用单因子方差分析ANOVA，下面对初中数学教师在CK（学科内容知识）在职称方面的差异进行分析。结果如表6.8所示。

表6.8　CK职称差异分析

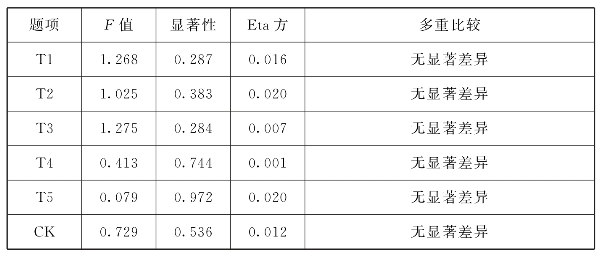
表6.8显示，CK职称差异检验的F＝0.729，p＝0.536＞0.05，未达到显著性水平，Eta方为0.012，初中数学教师CK与教师职称的关联度为1.2%，关联度很低。通过各题目的LSD多重比较分析可以看出，CK在教师职称上无明显差异。

（5）CK就职区域差异分析

将教师就职区域分为农村（A）、城镇（B）和市区（C），采用单因子方差分析ANOVA，下面对初中数学教师CK（学科内容知识）在就职区域方面的差异进行分析。结果如表6.9、表6.10所示。

表6.9　CK就职区域的均值、标准差、标准误

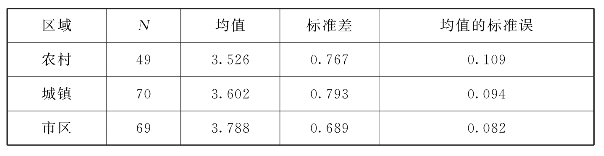
表6.10　CK就职区域差异分析

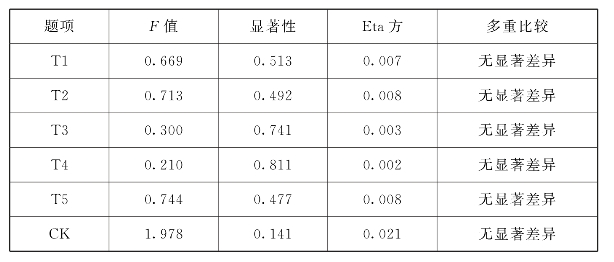
从表6.9看出农村教师CK分数为3.5265，城镇教师CK分数为3.6029，市区教师CK分数为3.7884，市区＞城镇＞农村，这与不同地区发展水平和教师师资力量有关。表6.10显示，CK职称差异检验的F＝1.978，p＝0.141＞0.05，未达到显著性水平，Eta方为0.021，初中数学教师CK测试题平均得分与教师职称的关联度为2.1%，关联度很低。通过各题目的LSD多重比较分析看出，CK在教师就职区域上无明显差异。

（6）CK学历差异分析

将教师学历分为：专科及以下（A）、本科（B）、硕士（C）、博士（D）以及其他（E），由于调查对象中学历为博士、其他的人数过少，因此只对前3种采用单因子方差分析ANOVA，下面对初中数学教师在CK在年级的差异进行分析。结果如表6.11所示。

表6.11　CK学历差异分析

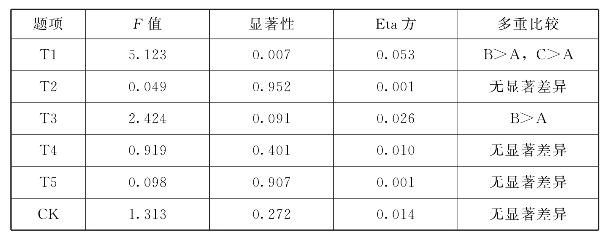
表6.11显示，CK学历差异检验的F＝1.313，p＝0.272＞0.05，未达到显著性水平，Eta方为0.014，初中数学教师CK测试题平均得分与教师学历的关联度为1.4%。但在基础知识上，F＝5.123，p＝0.007＜0.05，达到显著水平，学历为硕士（C）和本科（B）比学历为专科及以下（A）的教师有更好的平面图形变换的基础知识。在地位和作用的认识上，F＝2.424，p＝0.091，学历为本科（B）比学历为专科及以下（A）的教师能更好地认识平面图形变换的地位作用。

6.PK（教学法知识）发展差异分析

（1）PK各题平均分差异分析

PK是整合信息技术的学科教学知识的核心知识之一，同样也是构成的基础。图6.2为初中数学知识平面图形变换的PK知识的得分情况。

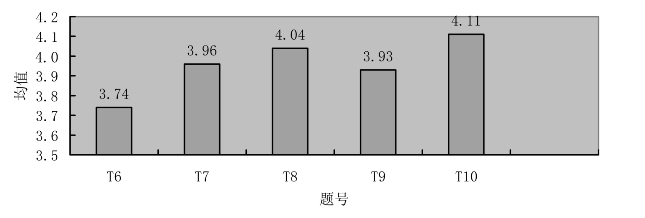
图6.2　PK测试题平均得分

从图6.2中数据可以看出，PK中各题目初中数学教师分值处于偏上水平。这5题分别是测试教师对教学方法的运用、对学情能否正确分析、是否抓住教学重难点、学生评价以及课堂管理。后四项分数较高，说明教师的自信度很高，教学能力比较强。T6分数最低为3.74，说明教师在对于教学方法的灵活使用上有所欠缺，需要不断加强。T10分数最高为4.11，在课堂管理上很有信心，有自己擅长的方法。T7、T8、T9分数较高，但也有待提高。

（2）PK性别差异分析

下面对PK（教学法知识）在性别方面的差异进行差异分析，运用SPSS 22.0进行独立样本t检验，结果如表6.12所示。

表6.12　PK性别差异分析

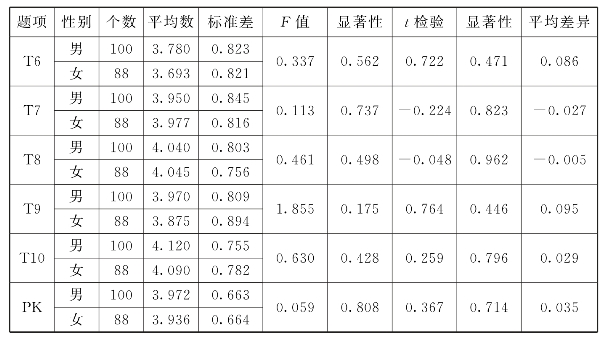
注：T6：教学方法，T7：教学计划，T8：重难点，T9：教学评价，T10：课堂管理。

对各题男女平均分进行比较，在T6：教学方法、T9：教学评价、T10：课堂管理，男性得分高于女性得分。而在T7：教学计划，T8：重难点上，女性得分明显高于男性得分。在PK得分上男性高于女性，男性得分为3.972，女性得分为3.936。经过双重t检验，t值等于0.367，男性大于女性，说明初中数学教师PK在性别上没有显著差异。并且初中数学教师在PK其他各题目也没有明显的性别差异。

（3）PK教龄差异分析

将教龄分为：0～5年（A）、6～10年（B）、11～15年（C）以及16年及以上（D），为连续变量，采用单因子方差分析ANOVA，下面对初中数学教师在PK（教学法知识）在教龄方面的差异进行分析，结果如表6.13所示。

表6.13　PK教龄差异分析

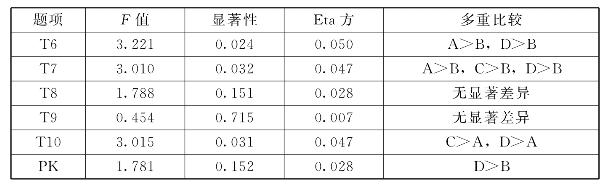
表6.13显示，PK教龄差异检验的F＝1.781，p＝0.152＞0.05，未达到显著性水平，Eta方为0.028，初中数学教师PK与教师年龄的关联度为12.8%，关联度低。通过各题目的LSD多重比较分析看出，教龄在16年及以上（D）比教龄在6～10年（B）教师有更好的教学方法知识，但差异并不显著。在教学方法上，F＝3.221，p＝0.024＜0.05，达到显著水平，教龄为0～5年（A）和16年及以上（D）的教师比教龄为“6～10年（B）”教学方法更灵活。在教学计划的编写上，F＝3.010，p＝0.032＜0.05，达到显著水平，教龄为0～5年（A）、11～15年（C）和16年及以上（D）教师均比教龄为6～10年（B）教师拥有更好的教学计划编写能力。在课堂管理上，F＝3.015，p＝0.031＜0.05，达到显著水平，教龄为11～15年（C）和16年及以上（D）的教师比教龄为0～5年（A）教师课堂管理能力更强。在教学计划的编写上，无显著差异。

（4）PK职称差异分析

将教师职称分为：中教三级（A）、中教二级（B）、中教一级（C）、高级（D），采用单因子方差分析ANOVA，下面对初中数学教师PK（教学法知识）在职称方面的差异进行分析，结果如表6.14所示。

表6.14　PK职称差异分析

表6.14显示，PK的职称差异检验F＝1.100，p＝0.351＞0.05，未达到0.05显著性水平，初中数学教师PK在职称上没有明显的差异。Eta方为0.018，说明关联度为1.8%，关联度低。但是在教学方法上，F＝2.810，p＝0.041＜0.05，达到显著水平，职称为高级（D）的教师比职称为中教二级（B）和中教一级（C）的教师教学方法更灵活。在教学计划编写上，F＝3.880，p＝0.010＜0.05，达到显著水平，职称为高级（D）的教师比职称为中教二级（B）和中教一级（C）的教师计划能力更强。在重难点把握上，F＝1.534，p＝0.207＞0.05，职称为高级（D）的教师比职称为中教一级（C）的教重难点掌握能力更强，但差异并不明显。

（5）PK就职区域差异分析

将教师就职区域分为：农村（A）、城镇（B）和市区（C），采用单因子方差分析ANOVA，下面对初中数学教师PK（教学知识）在就职区域方面的差异进行分析，结果如表6.15所示。

表6.15　PK区域差异分析

表6.15显示，PK就职区域差异检验的F＝2.914，p＝0.0057＞0.05，未达到显著性水平，Eta方为0.031，初中数学教师PK与教师年龄的关联度为3.1%，关联程度低。通过各题目的LSD多重比较分析看出，市区（C）的教师比农村（A）教师PK知识更灵活，但未达到显著水平。在教学方法上，F＝2.552，p＝0.081＞0.05，市区（C）的教师比城镇（B）教师教学方法更灵活，但未达到显著水平。在教学计划编写上，F＝3.098，p＝0.047＜0.05，达到显著水平，市区（C）教师比城镇（B）教师教学计划编写能力更强。

（6）PK学历差异分析

将教师学历分为：专科及以下（A）、本科（B）、硕士（C）、博士（D）以及其他（E），由于调查对象中学历为博士、其他的人数过少，因此只对前3种采用单因子方差分析ANOVA，下面对初中数学教师PK在学历上的差异进行分析。结果如表6.16所示。

表6.16　PK学历差异分析

表6.16显示，PK学历差异检验的F＝0.191，p＝0.826＞0.05，未达到显著性水平，Eta方为0.002，初中数学教师PK与教师学历的关联度为0.2%。通过各题目的LSD多重比较分析看出，PK在学历上没有显著差异。

7.TK（技术知识）发展差异分析

（1）TK各题平均分差异分析

技术知识是TPACK知识的基础知识，也是TPACK知识中最灵活的部分。直接影响着TPACK知识的整体水平。图6.3为初中数学知识平面图形变换的TK知识的得分情况。

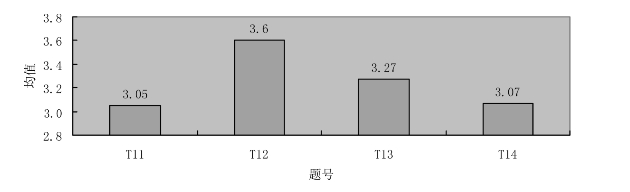
图6.3　TK测试题平均得分

从图6.3可以看出，技术知识的4个题目得分均在4分以下。T11的分数为3.05，说明初中数学教师对自身解决信息技术问题的自信度差。T12分数说明初中数学教师对信息技术的认同度还是很高的，并且愿意花时间去学习信息技术。T13说明初中数学教师对信息技术的更新能力一般，对信息技术兴趣不够。没有花费大量时间了解最新信息技术。T14分数为3.07，说明初中数学教师对信息技术软件的使用能力偏低。这些问题出现的原因可能在于初中数学教师对信息技术系统的学习不够，对信息技术没有全面的认识。

（2）TK性别差异分析

下面对TK（技术知识）在性别方面的差异进行差异分析，需进行独立样本t检验，结果如表6.17所示。

表6.17　TK性别差异分析

注：T11：硬件处理，T12：信息意识，T13：信息技术更新，T14：软件使用。

表6.17中，除T13外，TK的其余各题分数女性均高于男性。男、女在信息技术方面的平均数分别为3.202、3.301，女性略高于男性。经过双重t检验，t值等于－0.703，p＝0.483＞0.05，说明初中数学教师在性别上没有显著差异。

（3）TK教龄差异分析

将教龄分为：0～5年（A）、6～10年（B）、11～15年（C）和16年及以上（C），为连续变量，采用单因子方差分析ANOVA，下面对初中数学教师在TK（技术知识）在教龄方面的差异进行分析。应采用LSD多重比较法进行教龄差异分析，结果如表6.18所示。

表6.18　TK教龄差异分析

表6.18显示，TK教龄差异检验的F＝4.191，p＝0.007＜0.05，达到显著性水平，Eta方为0.064，初中数学教师TK与教师教龄的关联度为6.4%，达到低度关联程度。通过多重比较，教龄为0～5年（A）、16年及以上（D）的教师比教龄为6～10年（B）的教师技术知识更牢固。在对于硬件问题的处理上，F＝3.135，p＝0.027＜0.05，达到显著水平，教龄为0～5年（A）的教师比教龄为6～10年（B）和16年及以上（D）硬件处理问题能力更强。在信息技术的使用意识上，F＝6.003，p＝0.001＜0.05，达到显著水平，教龄为0～5年（A）、11～15年（C）和16年及以上（D）教师均比教龄为6～10年（B）教师拥有更强的信息技术使用意识。在软件使用上，F＝3.106，p＝0.028＜0.05，达到显著水平。教龄为0～5年（A）的教师比教龄为6～10年（B）和11～15年（C）的教师拥有更强的软件使用能力。

（4）TK职称差异分析

将教师职称分为：中教三级（A）、中教二级（B）、中教一级（C）以及高级（D），采用单因子方差分析，下面对初中数学教师在TK（技术知识）在职称方面的差异进行分析，结果如表6.19所示。

表6.19　TK职称差异分析

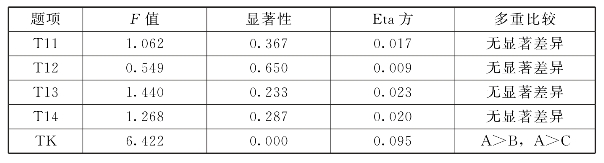
表6.19显示，TK的职称差异检验F＝6.422，p＝0.000＜0.05，初中数学教师TK在职称上具有明显的差异。Eta方为0.095，说明关联度为9.5%，达到了中强度关联。职称为中教三级（A）的教师比职称为中教二级（B）和中教一级（C）的教师信息技术知识更牢固。但是在TK所包含的四个问题上显著性均大于0.05，未达到显著性水平。

（5）TK就职区域差异分析

将教师就职区域分为：农村（A）、城镇（B）和市区（C），采用单因子方差分析，下面对初中数学教师在TK（技术知识）在就职区域方面的差异进行分析。结果如表6.20所示。

表6.20　TK区域差异分析

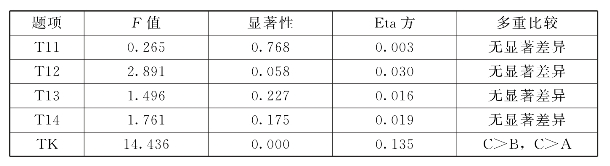
表6.20显示，TK就职区域差异检验的F＝14.436，p＝0.000＜0.05，达到显著性水平，Eta方为0.135，初中数学教师TK与教师就职区域的关联度为13.5%，达到中高度关联程度。多重比较分析看出，市区（C）的教师比农村（A）和城镇（B）的教师有更牢固的信息技术知识。在TK所包含的四个问题上显著性均大于0.05，未达到显著性水平。

（6）TK学历差异分析

将教师学历分为：专科及以下（A）、本科（B）、硕士（C）、博士（D）以及其他（E），由于调查对象中学历为博士、其他部分人数过少，因此只对前3种采用单因子方差分析ANOVA，下面对初中数学教师TK在年级的差异进行分析，结果如表6.21所示。

表6.21　TK学历差异分析

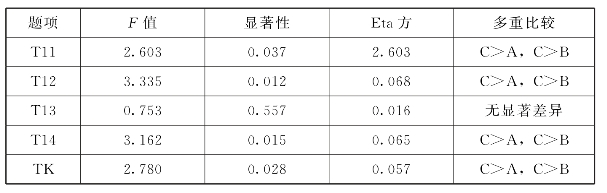
表6.21显示，TK学历差异检验的F＝2.780，p＝0.028＜0.05，达到显著性水平，Eta方为0.028，初中数学教师TK与教师学历的关联度为2.8%。通过各题目的LSD多重比较分析看出，学历为硕士（C）比学历为专科及以下（A）和本科（B）的教师有更牢固的信息技术知识。并且在硬件处理上，F＝2.780，p＝0.037＜0.05，达到显著性水平，学历为硕士（C）的教师比学历为专科及以下（A）和本科（B）的教师有更强的硬件处理能力。在信息技术的使用意识上，F＝3.335，p＝0.012＜0.05，达到显著性水平，学历为硕士（C）的教师比学历为专科及以下（A）和本科（B）的教师有更强的信息技术的使用意识。对于软件使用，学历为硕士（C）的教师比学历为专科及以下（A）和本科（B）的教师能力更强，达到显著水平。

8.PCK（学科教学知识）发展差异分析

（1）PCK各题平均分差异分析

PCK（学科教学知识）是学科内容知识与教学法知识复合而成。是教师平面图形变换教学能力的直接体现。图6.4为初中数学知识平面图形变换的PCK知识的得分情况。

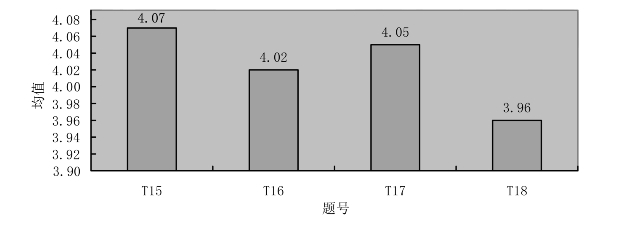
图6.4　PCK测试题平均得分

T15是测试对平面图形变换的基本概念的教学能力，分数为4.07，说明教师能理解基本概念，做好基础工作。T16是考察平面图形变换的基本方法教学能力，分数为4.02，说明教师能掌握学习该内容需要的方法，并且能进行优质的教学。T17是考察平面图形变换的系统关系教学能力，分数为4.05，说明教师能很好地将平移、轴对称、旋转等内容联系起来，帮助学生建立系统框架。T18是考察平面图形变换的解题方法教学能力，分数为3.96，分数略低，但也能看出教师对于解题教学也是比较擅长的。

（2）PCK性别差异分析

下面分析PCK（学科教学知识）在性别方面的差异，运用SPSS 22.0进行数据分析，结果如表6.22所示。

表6.22　PCK性别差异分析

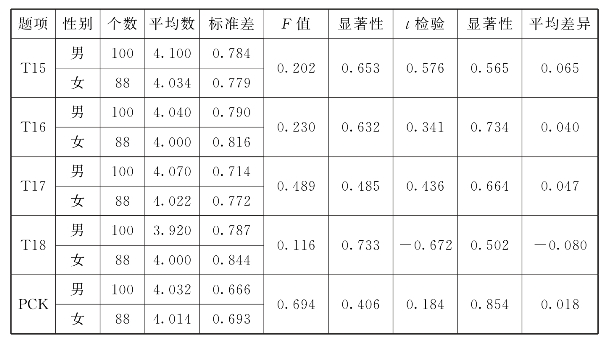
注：T15：平面图形变换知识的概念，T16：方法，T17：系统的知识框架，T18：解决实际问题。

对各题男女平均分进行比较，在T15：平面图形变换知识的概念，T16：方法，T17：系统的知识框架上，男性得分高于女性。而在T18：解决实际问题，女性略高于男性。男性PCK得分为4.0325，女性得分为4.0142，得分均在4以上，处于偏上水平，男性高于女性。经过双重t检验，t值等于0.184，p＝0.854＞0.05，说明初中数学教师PCK在性别上没有显著差异，并且初中数学教师在PCK包含各题目上也没有明显的性别差异。

（3）PCK教龄差异分析

将教龄分为：0～5年（A）、6～10年（B）、11～15年（C）以及16年及以上（C），下面对PCK（学科教学知识）在教龄方面的差异进行差异分析，运用SPSS 22.0进行数据分析，结果如表6.23所示。

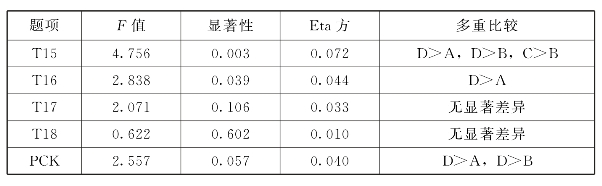
表6.23　PCK教龄差异分析

(www.zuozong.com)

表6.23显示，PCK教龄差异检验的F＝2.557，p＝0.057＞0.05，未达到显著性水平，Eta方为0.040，初中数学教师PCK与教师教龄的关联度为4.0%，关联度低。通过各题目的LSD多重比较分析看出，教龄在16年及以上（D）比教龄为0～5年（A）和6～10年（B）教师有更好的平面图形变换教学方法知识，但其差异并不明显。在平面图形变换知识的概念教学上，F＝4.756，p＝0.003＜0.05，达到显著水平，教龄为16年及以上（D）的教师明显比教龄为0～5年（A）和6～10年（B）概念教学更灵活，并且在概念教学上，教龄为11～15年（C）的教师比教龄为6～10年（B）教龄的教师更擅长。在平面图形变换知识的方法教学上，F＝2.838，p＝0.039＜0.05，达到显著水平，教龄为16年及以上（D）的教师明显比教龄为0～5年（A）的教师方法教学能力更强。

（4）PCK职称差异分析

将教师职称分为：中教三级（A）、中教二级（B）、中教一级（C）以及高级（D），下面对PCK（学科教学知识）在职称方面的差异进行差异分析，运用SPSS 22.0进行数据分析，结果如表6.24所示。

表6.24　PCK职称差异分析

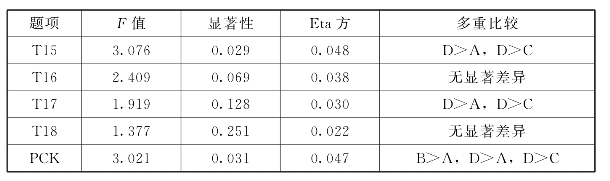
表6.24显示，PCK的职称差异检验F＝3.021，p＝0.031＜0.05，达到显著性水平，初中数学教师PCK在职称上有明显的差异。Eta方为0.047，说明关联度为4.7%，达到中低关联程度。多重比较分析看出，职称为中教二级（B）的教师比职称为中教三级（A）平面图形变换的教学能力更强。职称为高级（D）的教师比职称为中教三级（A）和中教一级（C）的教师有更好的平面图形变换教学方法知识。在平面图形变换知识的概念教学上，F＝3.076，p＝0.029＜0.05，达到显著水平，职称为高级（D）的教师比职称为中教三级（A）和中教一级（C）的教师概念教学更灵活。在平面图形变换知识系统的知识框架的掌握上，p值为0.128，大于0.05，职称为高级（D）的教师比职称为中教三级（A）和中教一级（C）的教师更擅长，但未达到显著水平。

（5）PCK就职区域差异分析

将教师就职区域分为：农村（A）、城镇（B）和市区（C），采用单因子方差分析ANOVA，下面就PCK（学科教学知识）在就职区域方面的差异进行差异分析，结果如表6.25所示。

表6.25　PCK区域差异分析

表6.25显示，PCK就职区域差异检验的F＝3.939，p＝0.021＜0.05，达到显著性水平，Eta方为0.041，初中数学教师PCK与教师区域的关联度为4.1%，关联程度低。通过各题目的LSD多重比较分析看出，市区（C）的教师比农村（A）和城镇（B）教师PCK知识更丰富。这与不同地区发展水平和师资力量有关。说明地区越发达，初中数学教师在平面图形变换的教学能力越强。在PCK所包含的各问题上并没有显著差异。

（6）PCK学历差异分析

将教师学历分为：专科及以下（A）、本科（B）、硕士（C）、博士（D）以及其他（E），由于调查对象中学历为博士、其他过少，因此只对前3种采用单因子方差分析ANOVA，下面对初中数学教师在PCK在年级的差异进行分析。结果如表6.26所示。

表6.26　PCK学历差异分析

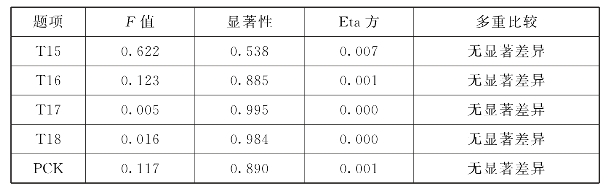
表6.26显示，PCK学历差异检验的F＝0.117，p＝0.890＞0.05，未达到显著性水平，Eta方为0.001，初中数学教师PCK与教师学历的关联度为0.1%。通过各题目的多重比较，PCK在学历上没有显著差异。

9.TCK（整合技术的学科内容知识）发展差异分析

（1）TCK各题平均分差异分析

TCK是学科内容知识与技术知识复合而成。图6.5为初中数学知识平面图形变换的TCK知识的得分情况。

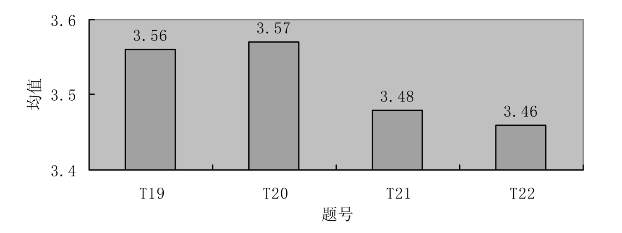
图6.5　TCK测试题平均得分

T19是测试运用信息技术获取平面图形变换资源的情况。T20是测试运用信息技术呈现特定的平面图形变换内容。T21：运用信息技术，直观展示平面图形的变换过程。T22：测试运用信息技术探求解决平面图形变换问题的思路。这四道题目得分均在3.6以下，得分较低。尤其是最后两道题得分过低。说明教师在信息技术与平面图形变换内容结合上存在不足，在教学中需要多尝试使用信息技术。

（2）TCK性别差异分析

下面对TCK（整合技术的学科内容知识）在性别方面的差异进行差异分析，运用SPSS 22.0进行数据分析，结果如表6.27所示。

表6.27　TCK性别差异分析

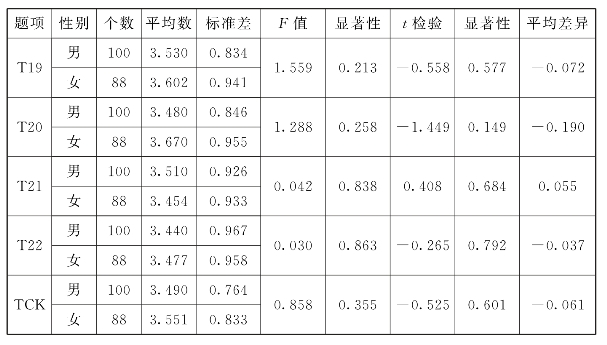
注：T19：运用信息技术拓宽知识，T20：呈现平面图形变换内容，T21：展示知识的动态过程，T22：借助信息技术解决问题。

对各题男女平均分进行比较，在T19：运用信息技术拓宽知识、T20：呈现平面图形变换内容、T22：借助信息技术解决问题上，女性得分略高于男性得分。而在T21：展示知识的动态过程上，男性得分高于女性得分。TCK男性得分为3.490，女性得分为3.551，得分均在4以下，得分偏低，女性高于男性，但差距并不大。经过双重t检验，t值等于－0.525，p＝0.601＞0.05，说明初中数学教师TCK在性别上没有显著差异。并且初中数学教师在TCK包含各题目上也没有明显的性别差异。

（3）TCK教龄差异分析

将教龄分为：0～5年（A）、6～10年（B）、11～15年（C）以及16年及以上（C），下面对TCK（整合技术的学科知识）在教龄方面的差异进行差异分析，运用SPSS 22.0进行数据分析，结果如表6.28所示。

表6.28　TCK教龄差异分析

表6.28显示，TCK教龄差异检验的F＝1.462，p＝0.227＞0.05，未达到显著性水平，Eta方为0.023，初中数学教师TCK与教师教龄的关联度为2.3%，关联度低。通过各题目的LSD多重比较分析看出，在教龄上TCK并没有显著差异。在T21：展示知识的动态过程，T22：借助信息技术解决问题但是展示知识的动态过程上，F＝1.509，p＝0.214＞0.05，未达到显著水平，教龄为16年以上（D）的教师明显比教龄为0～5年（A）的教师更擅长，但差异不明显。在借助信息技术解决问题上，F＝2.551，p＝0.057，略大于0.05，教龄为16年以上（D）的教师明显比教龄为0～5年（A）和11～15年（C）的教师解决问题能力强，但差异不明显。在T19：运用信息技术拓宽知识，T20：呈现平面图形变换内容上，也没有显著的差异。

（4）TCK职称差异分析

将教师职称分为：中教三级（A）、中教二级（B）、中教一级（C）以及高级（D），采用单因子方差分析ANOVA，下面对TCK（整合技术的学科知识）在职称方面的差异进行差异分析，运用SPSS 22.0进行数据分析，结果如表6.29、表6.30所示。

表6.29　TCK职称的均值、标准差和标准误

表6.30　TCK职称差异分析

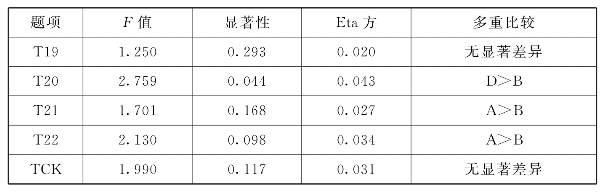
表6.29中数据显示得分均在3.5分以上，分值不高。随着职称的不断提高，初中数学教师在平面图形变换中教学中的TCK得分呈现出两边高、中间低的趋势。表6.30显示，TCK职称差异检验的F＝1.990，p＝0.117＞0.05，未达到显著性水平，Eta方为0.031，初中数学教师TCK与教师年龄的关联度为3.1%，关联度低。通过各题目的LSD多重比较分析可以看出，在职称上TCK并没有显著差异。但在T20：呈现平面图形变换内容，F＝2.759，p＝0.044＜0.05，达到显著水平，职称为高级（D）的教师比职称为中教二级（B）的教师更擅长用信息技术呈现平面图形变换内容。在T21：展示知识的动态过程，T22：借助信息技术解决问题上，p值分别为0.168、0.098，均大于0.05，职称为中教三级（A）的教师比职称为中教二级（B）的教师更擅长，但未达到显著水平。

（5）TCK就职区域差异分析

将教师就职区域分为：农村（A）、城镇（B）和市区（C），采用单因子方差分析ANOVA，下面分析TCK（技术知识）在就职区域方面的差异，运用SPSS 22.0进行数据分析，结果如表6.31所示。

表6.31　TCK区域差异分析

表6.31显示，TCK就职区域差异检验的F＝1.908，p＝0.151＞0.05，未达到显著性水平，Eta方为0.020，初中数学教师TCK与教师就职区域的关联度为2.0%，关联程度低。通过各题目的LSD多重比较分析可以看出，在就职区域上TCK没有显著差异。但在T20：呈现平面图形变换内容，F＝3.143，p＝0.045＜0.05，达到显著水平，就职区域在农村（A）的教师比就职区域在城镇（B）的教师更擅长用信息技术呈现平面图形变换内容。

（6）TCK学历差异分析

将教师学历分为：专科及以下（A）、本科（B）、硕士（C）、博士（D）以及其他（E），由于调查对象中学历为博士、其他的人数过少，因此只对前3种采用单因子方差分析ANOVA，下面对初中数学教师在TCK在学历上的差异进行分析，结果如表6.32所示。

表6.32　TCK学历差异分析

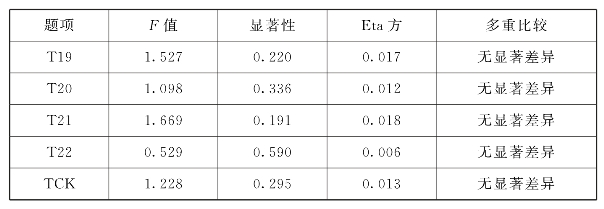
表6.32显示，TCK学历差异检验的F＝1.228，p＝0.295＞0.05，未达到显著性水平，Eta方为0.013，初中数学教师TCK与教师学历的关联度为1.3%。通过各题目的LSD多重比较分析可以看出，TCK在学历上没有显著差异。

10.TPK（学科教学知识）发展差异分析

（1）TPK各题平均分差异分析

TPK（学科教学知识）也是整合技术的学科教学知识的复合知识部分，是教学法知识与技术知识复合而成。图6.6为初中数学知识平面图形变换的TPK知识的得分情况。

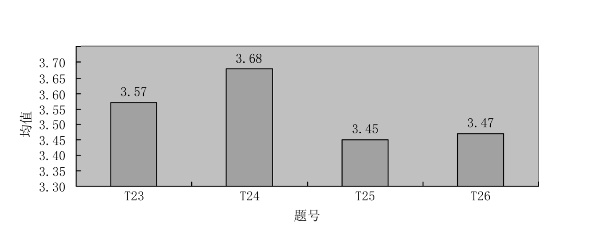
图6.6　TPK测试题平均得分

这四道题目分别是对信息技术条件下课前编写教学计划、课堂教学、课后教学反思以及课后学生评价工作的测试。这四道题目得分均在3.7以下，得分较低。根据分值可以看出初中数学教师在平面图像变换的教学中，课前、课后信息技术的使用效率低，不能充分地借助信息技术进行辅助教学工作。在课堂教学中初中数学教师对信息技术使用熟练，但仍需加强。

（2）TPK性别差异分析

下面分析TPK（学科教学知识）在性别方面的差异，运用SPSS 22.0进行数据分析，结果如表6.33所示。

表6.33　TPK性别差异分析

注：T23：信息技术辅助备课，T24：提高课堂教学效率，T25：批判性地选择和使用信息技术，T26：课后辅导及学生评价。

对各题男女平均分进行比较，在T24：提高课堂教学效率，T25：批判性地选择和使用信息技术上，女性得分高于男性得分。而在T23：信息技术辅助备课、T26：课后辅导及学生评价上，男性得分高于女性得分。TPK男性得分为3.532，女性得分为3.559，得分均在4以下，得分偏低，女性得分高于男性得分，但差距并不大。经过双重t检验，t值等于－0.249，p＝0.804＞0.05，说明初中数学教师TPK在性别上没有显著差异。并且初中数学教师在TPK包含各题目上也没有明显的性别差异。

（3）TPK教龄差异分析

将教龄分为：0～5年（A）、6～10年（B）、11～15年（C）以及16年及以上（C），采用单因子方差分析ANOVA，下面分析TPK（学科教学知识）在教龄方面的差异，结果如表6.34所示。

表6.34　TPK教龄差异分析

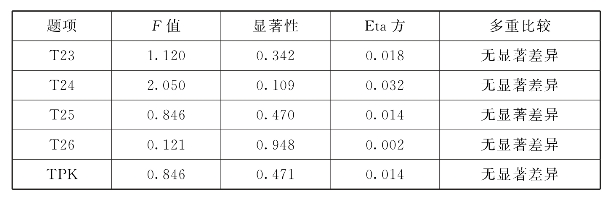
表6.34显示，TPK教龄差异检验的F＝0.846，p＝0.471＞0.05，未达到显著性水平，Eta方为0.014，初中数学教师TPK与教师年龄的关联度为1.4%，关联程度低。

（4）TPK职称差异分析

将教师职称分为：中教三级（A）、中教二级（B）、中教一级（C）以及高级（D），采用单因子方差分析ANOVA，下面分析TPK（学科教学知识）在职称方面的差异，运用SPSS 22.0进行数据分析，结果如表6.35所示。

表6.35　TPK职称差异分析

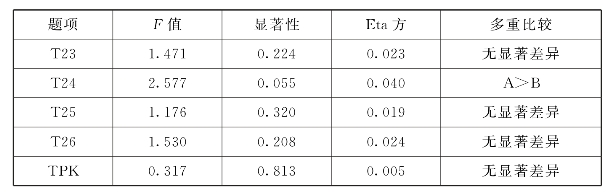
表6.35显示，TPK职称差异检验的F＝0.317，p＝0.813＞0.05，未达到显著性水平，Eta方为0.005，初中数学教师TPK与教师职称的关联度为0.5%，关联程度低。通过各题目的LSD多重比较分析可以看出，在就职区域上TPK没有显著差异。但在T24：提高课堂教学效率，F＝2.577，p＝0.055＞0.05，未达到显著水平，职称为中教三级（A）的教师比职称为中教二级（B）的教师更能利用信息技术来提高教学效率。

（5）TPK就职区域差异分析

将教师就职区域分为：农村（A）、城镇（B）和市区（C），采用单因子方差分析ANOVA，下面对初中数学教师TPK（技术知识）在就职区域方面的差异进行分析，结果如表6.36、表6.37所示。

表6.36　TPK区域的均值、标准差和标准误

表6.37　TPK区域差异分析

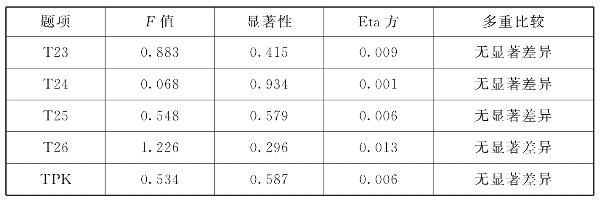
表6.36中数据显示均值整体偏低，农村教师TPK分数为3.479，城镇教师TPK分数为3.521，市区教师TPK分数为3.615，分值排序为：市区＞城镇＞农村。表6.37中，TPK就职区域差异检验的F＝0.534，p＝0.587＞0.05，未达到显著性水平，Eta方为0.006，初中数学教师TPK与教师年龄的关联度为0.6%，关联程度低。通过各题目的LSD多重比较分析可以看出，在就职区域上教师TPK没有显著差异。

（6）TPK学历差异分析

将教师学历分为：专科及以下（A）、本科（B）、硕士（C）、博士（D）以及其他（E），由于调查对象中学历为博士、其他的人数过少，因此只对前三种采用单因子方差分析ANOVA，下面对初中数学教师TPK在年级的差异进行分析，结果如表6.38所示。

表6.38　TPK学历差异分析

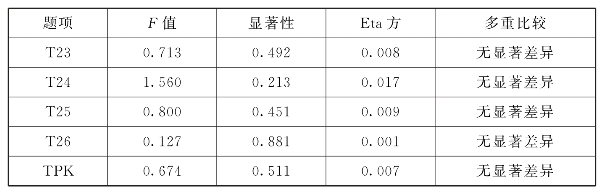
表6.38显示，TPK学历差异检验的F＝0.674，p＝0.511＞0.05，未达到显著性水平，Eta方为0.007，初中数学教师TPK与教师学历的关联度为0.7%。通过各题目的LSD多重比较分析可以看出，教师TPK在学历上没有显著差异。

11.TPACK（整合技术的学科教学知识）发展差异分析

（1）TPACK各题平均分差异分析

TPACK属于复合知识部分，图6.7为初中数学知识平面图形变换的TPACK知识的得分情况。

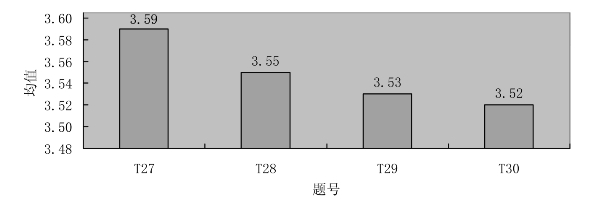
图6.7　TPACK测试题平均得分

这四道题目是对TPACK整体的测试，侧重点分别为教学方法、平面图形变换知识、信息技术以及整体要求。这四题的分数分别为3.59、3.55、3.53和3.52，依次降低。符合核心部分知识得分的排序情况，运用信息技术进行平面图形变换教学的整体要求的测试分数最低，要满足整体的要求是最难的。

（2）TPACK性别差异分析

下面分析TPACK在性别方面的差异，对其进行数据分析，结果如表6.39所示。

表6.39　TPACK性别差异分析

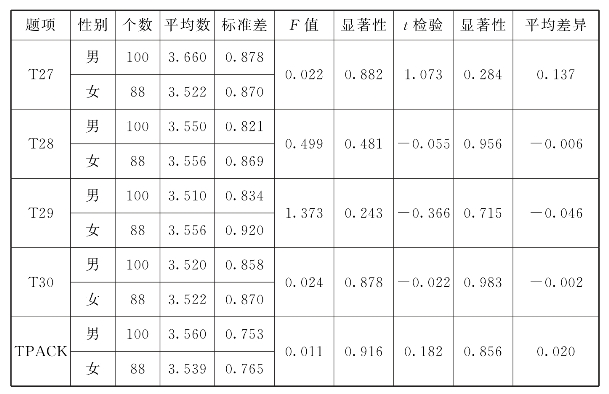
注：T27：有限性，T28：融合在课堂，T29：及时总结，T30：整体要求。

对各题男女平均分进行比较，在T28：融合在课堂，T29：及时总结，T30：整体要求上，女性高于男性。而在T27：有限性上，男性高于女性。TPACK男性得分为3.560，女性得分为3.539，得分均在4以下，得分偏低，男性高于女性，但差距并不大。经过双重t检验，t值等于0.182，p＝0.856＞0.05，说明初中数学教师TPACK在性别上没有显著差异，并且在TPACK包含各题目上也没有明显的性别差异。

（3）TPACK教龄差异分析

将教龄分为0～5年（A）、6～10年（B）、11～15年（C）以及16年及以上（C），为连续变量，采用单因子方差分析ANOVA，下面分析TPACK在教龄方面的差异，进行数据分析，结果如表6.40、表6.41所示。

表6.40　TPACK教龄的均值、标准差和标准误

表6.41　TPACK教龄的差异分析

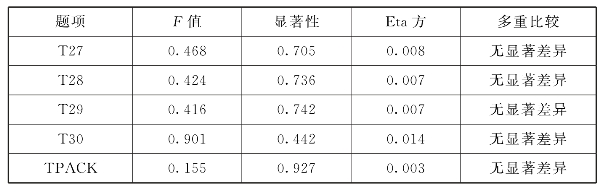
表6.40显示，TPACK随着教龄的逐渐增长呈现持续下降的趋势，教龄在0～5年与教龄6～10年均值大小相当，教龄在11～15年与教龄16年及以上均值大小相当。表6.41显示TPACK教龄差异检验的F＝0.155，p＝0.927＞0.05，未达到显著性水平，Eta方为0.003，初中数学教师TPACK与教龄的关联度为0.3%，关联度低。通过各题目的LSD多重比较分析可以看出，虽然均值有一定差距，但在教龄上TPACK差异并不显著。

（4）TPACK职称差异分析

将教师职称分为中教三级（A）、中教二级（B）、中教一级（C）以及高级（D），采用单因子方差分析ANOVA，下面对初中数学教师TPACK在职称方面的差异进行分析，结果如表6.42、表6.43所示。

表6.42　TPACK职称的均值、标准差和标准误

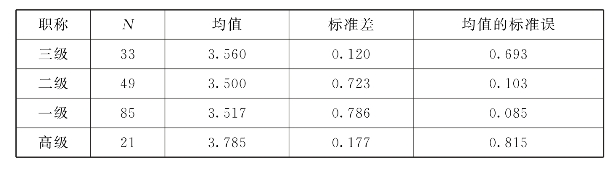
表6.43　TPACK职称的差异分析

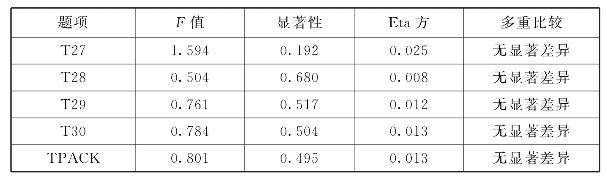
表6.42显示，得分均在3.5分以上，分值不高。随着职称的不断提高，初中数学教师在平面图形变换中教学中的TPACK得分逐渐增加。根据表6.43，TPACK职称差异检验的F＝0.801，p＝0.495＞0.05，未达到显著性水平，Eta方为0.013，初中数学教师TPACK与教师职称的关联度为1.3%，关联度低。通过各题目的LSD多重比较分析可以看出，在职称上TPACK没有显著差异。并且初中数学教师在TPACK包含各题目上也没有明显的职称差异。

（5）TPACK就职区域差异分析

将教师就职区域分为农村（A）、城镇（B）和市区（C），采用单因子方差分析ANOVA，下面对初中数学教师TPACK在就职区域方面的差异进行分析，结果如表6.44、表6.45所示。

表6.44　TPACK就职区域的均值、标准差和标准误

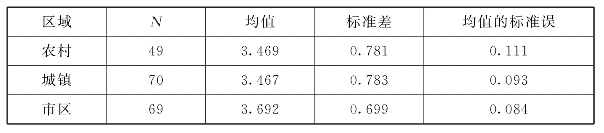
表6.45　TPACK就职区域的差异分析

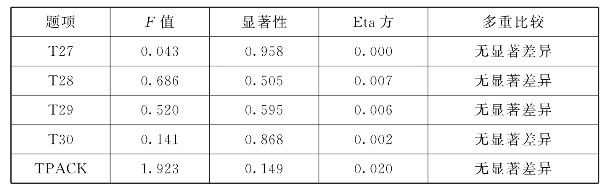
表6.44中数据显示，均值处于中等，农村教师TPACK分数为3.469，城镇教师TPACK分数为3.467，市区教师TPACK分数为3.692，分值排序为市区＞农村＞城镇，农村和城镇分值相当，市区分值略高。表6.45中数据显示TPACK就职区域差异检验的F＝1.923，p＝0.149＞0.05，未达到显著性水平，Eta方为0.02，初中数学教师TPACK与教师就职区域的关联度为2.0%，关联程度低。通过各题目的LSD多重比较分析可以看出，在就职区域上TPACK没有显著差异。

（6）TPACK学历差异分析

将教师学历分为专科及以下（A）、本科（B）、硕士（C）、博士（D）以及其他（E），由于调查对象中学历为博士、其他过少，因此只对前3种采用单因子方差分析ANOVA，下面对初中数学教师TPACK在学历的差异进行分析，结果如表6.46所示。

表6.46　TPACK学历差异分析

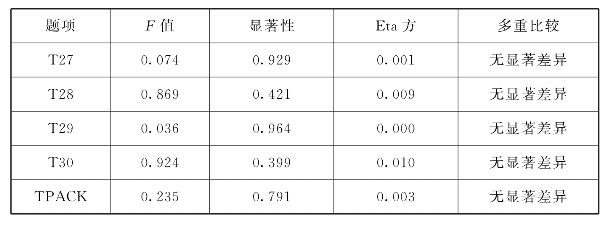
表6.46显示，TPACK学历差异检验的F＝0.235，p＝0.791＞0.05，未达到显著性水平，Eta方为0.003，初中数学教师TPACK与教师学历的关联度为0.3%。通过各题目的LSD多重比较分析可以看出，TPACK在学历上没有显著差异。

12.初中数学教师TPACK的整体相关性

使用SPSS 22.0对初中数学教师TPACK进行整体积差相关性分析，相关系数如表6.47所示。

表6.47　整体积差相关性

注：**相关性在0.01（双侧）水平上显著。*相关性在0.05（双侧）水平上显著。

表6.47中数据显示，初中数学教师TPACK与TK、CK、PK、PCK、TCK和TPK存在显著的正相关关系，显著性水平p＝0.000＜0.01，Pearson相关系数分别为0.387、0.540、0.467、0.432、0.699和0.846，表示与TPACK的相关性排序为TPK＞TCK＞CK＞PK＞PCK＞TK，与TPK的相关性最强。初中数学教师TK与CK、PK、PCK、TCK和TPK存在显著的正相关关系，显著性水平p＝0.000＜0.01，Pearson相关系数分别为0.522、0.304、0.273、0.410和0.369，说明TK好的教师，CK、PK、PCK、TCK和TPK也很好。初中数学教师CK与PK、PCK、TCK和TPK存在显著的正相关关系，显著性水平p＝0.000＜0.01，Pearson相关系数分别为0.554、0.459、0.630和0.515，说明CK好的教师，PK、PCK、TCK和TPK也很好。初中数学教师PK与PCK、TCK和TPK存在显著的正相关关系，显著性水平p＝0.000＜0.01，Pearson相关系数分别为0.733、0.493和0.472，说明PK好的教师，PCK、TCK和TPK也很好。初中数学教师PCK与TCK、TPK存在显著的正相关关系，显著性水平p＝0.000＜0.01，Pearson相关系数分别为0.458、0.393，说明PCK好的教师，TCK、TPK也很好。初中数学教师TCK与TPK存在显著的正相关关系，显著性水平p＝0.000＜0.01，Pearson相关系数为0.699，说明TCK好的教师，TPK也很好。

13.初中数学教师TPACK与不同背景的相关性

对初中数学教师的不同性别、教龄、职称、区域与初中数学教师TPACK及其构成要素进行相关性分析，结果如表6.48所示。

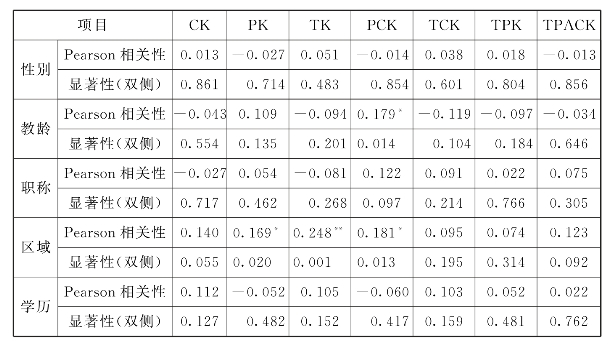
表6.48　初中数学教师TPACK发展的整体相关系数

注：**相关性在0.01（双侧）水平上显著。*相关性在0.05（双侧）水平上显著。

从表6.48中可以发现，初中数学教师PK与就职区域具有正相关性，p＝0.020＜0.05，说明城市教师具有更丰富的PK知识。初中数学教师TK与就职区域具有正相关性，p＝0.001＜0.01，说明城市教师具有更丰富的TK知识。教龄与初中数学教师PCK具有正相关性，p＝0.014＜0.05，说明教龄越长的教师具有更丰富的PCK知识。初中数学教师PCK与就职区域具有正相关性，p＝0.013＜0.05，说明城市教师具有更丰富的PCK知识。