基于VonKarman模型的湍流信号处理的方案

（1）三维湍流场产生

湍流场需要从频域变换到时域产生，图4.10中在频域空间把湍流场划分为M1×M2×M3个网格点。

根据离散傅里叶变换变换性质，则时域空间采样率和频域采样率二者之间的关系为

式中，vsi是ri方向上的时域采样率，Mi是在ri方向的网格点的数量，Δvi是在ri方向的频域空间上的网格间距。Δri是在ri方向上的时域网格间距。

图4.10　三维空间湍流场

图4.11　湍流场的生成

图4.11中，i＝1，2，3，ni（r1，r2，r3）为三路高斯白噪声序列，H（v1，v2，v3）表示三维成型滤波器函数，IDFT为逆三维离散傅里叶变换，wi（r1，r2，r3）表示各向同性湍流。

对于Von Karman模型，其自相关功率谱［126］为

式中，，Φii（v1，v2，v3）（i＝1，2，3）分别为纵向和两个横向的功率谱，a为定值1.339，σ是湍流强度，vi为三轴空间频率。

Von Karman模型的成型滤波器函数［172］为

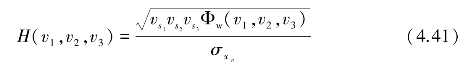
式（4.41）中，Φw（v1，v2，v3）是三维Von Karman频谱函数。

由于在实际的大气环境中，湍流尺度和强度是随着飞行高度而变化的，则可将空间距离无因次化，则有

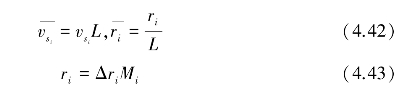
式中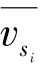，为无因次空间采样率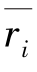；为无因次空间距离，L为湍流场尺度。用Lx表示x轴方向的湍流尺度，用Ly表示y轴方向的湍流尺度，用Lz表示z轴方向的湍流尺度。

根据空间频谱，表示空间波数。无因次频谱Φw可根据有因次频谱来得到，即

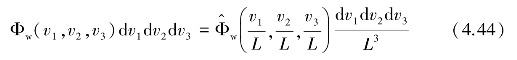
（2）湍流信号处理

三维离散傅里叶变换和反变换为

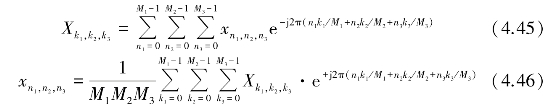
式中，ni＝0，1，…，Mi－1；ki＝0，1，…，Mi－1。其中，为三维傅里叶变换的时域数值序列，为三维傅里叶变换的频域数值序列。(www.zuozong.com)

设三维零均值时域噪声方差为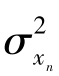，则三维零均值频域噪声方差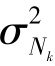为

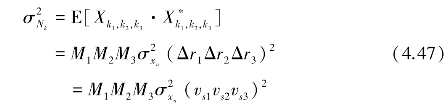
FFT的三维对称特性见表4.1。

表4.1　FFT三维对称特性

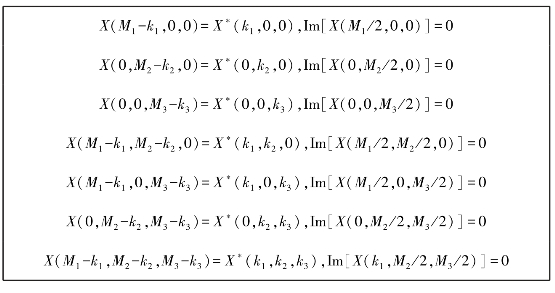
气象雷达湍流处理流程如图4.12所示。图4.12中，IDFT的目的是为了把产生的湍流数据转化到空域，这里需要说明的是产生三维频域噪声方差一定要满足式（4.47）的要求。

图4.12　机载雷达湍流处理流程图

（3）仿真结果分析

网格空间采用64×64×64，Lx＝40m；Ly＝Lz＝20m，脉冲重复频率为3 724Hz，发射平均功率为150W，距离门数为50，方位扫描中心为0°，俯仰扫描中心为－3°。

图4.13、图4.14分别为在无因次和有因次情形下的湍流仿真图。

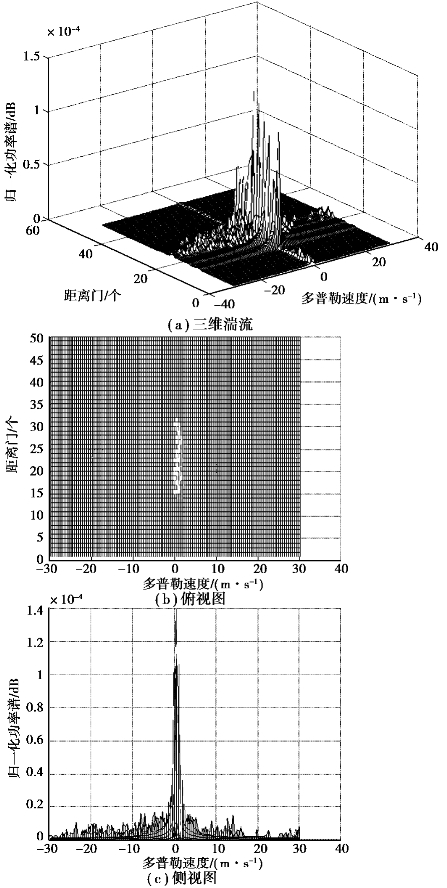
图4.13　无因次情形下的湍流仿真图

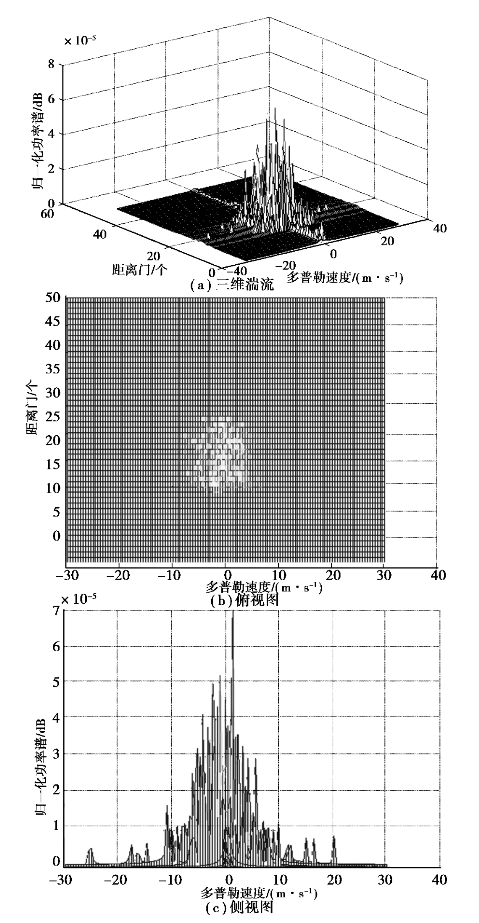
图4.14　有因次情形下的湍流仿真图

通过图4.13和图4.14可以看出，在湍流区域中，速度谱分布体现出“脉动”的特征，符合涡旋的基本特性，有因次情形下的湍流速度的波动规律与无因次的规律是类似的，但有因次的波动幅度要大于无因次情形。气象目标是由大量散射粒子组成的，是分布式目标。当雷达波照射时，大量粒子（具有随机相位）散射电场的叠加可得到一个高斯统计信号。由于粒子相互运动，故还存在一个多普勒谱方差，因此，气象目标的回波功率谱呈现近似高斯谱的特性。从图4.13和图4.14可以看出，仿真结果与理论分析是一致的，说明产生的湍流场数据是合理的。

用Vx表示X轴上的速度，Vy表示Y轴上的速度，Vz表示Z轴上的速度，则总的速度V为。各个方向上的风速以及总风速V的矢量估计图如图4.15所示。

设湍流检测门限为5m/s。图4.15仿真的是64×64×64网格空间上的第32根扫描线的风速。从图4.15（d）可以看出，网格点16，42处（即在点（32，40，16）和点（32，40，42）处）存在湍流目标。

图4.16是仿真了z＝32上的风速。其他情形下的风速值与图4.16相类似，都呈随机性的剧烈变化。

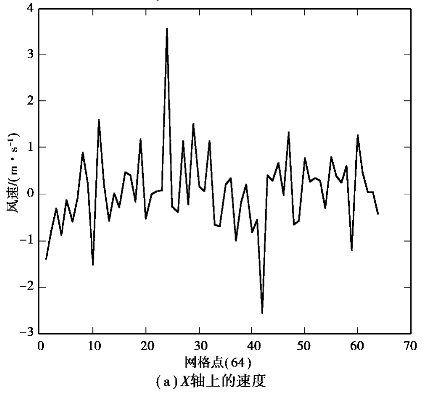
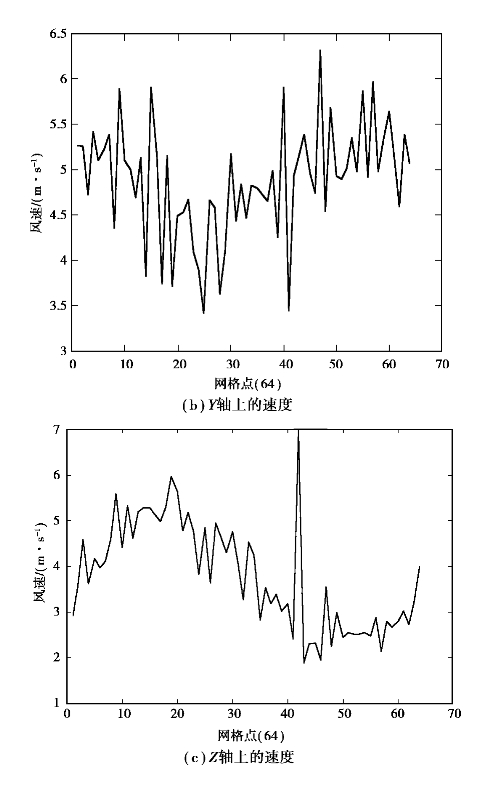
图4.15　风速矢量估计图（有因次）

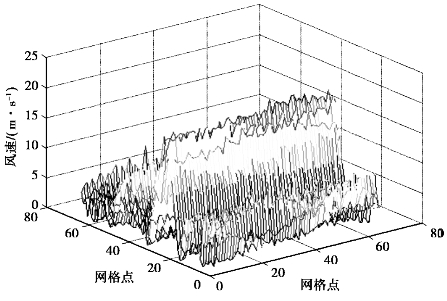
图4.16　三维湍流场图（有因次情形）