桨盘诱导速度的计算方法

旋翼桨盘平面的诱导速度直接影响翼型剖面迎角，是气动载荷的重要组成部分，而直升机飞行时靠近旋翼的尾迹形态决定了桨盘处的诱导速度分布，特别是低速飞行状态下，由于尾迹移动较慢，桨涡干扰严重，是气动载荷中高频成分的主要来源。对于动力学问题，简化的均匀入流模型不能够准确描述旋翼载荷的高阶谐波项，为了更精确的描述旋翼尾迹对桨叶动载荷的影响，本书采用Johnson自由尾迹模型。

将尾迹几何表示为

rW(ψ,φ)=rb(ψ-φ)+ψµ+D(ψ,φ)

上式rb为桨叶上径向站点r处的位置矢量，μ是自由速度的矢量。方程的第一项和第二项构成了尾迹几何的基本螺旋结构.

第三项表示自诱导速度引起的尾迹畸变。采用自由尾迹时需要考虑自由流和自诱导流场的影响，由于桨尖涡在尾迹计算中起决定作用，因此Johnson自由尾迹模型仅考虑桨尖涡的畸变，内部采用刚性或预定尾迹模型。尾迹几何的迭代过程首先需要计算所有涡元在给定涡龄φ和所有方位角Ψ处的诱导速度以，涡龄增加△φ，更新尾迹畸变为

D(ψ,φ)=D(ψ,φ-Δφ)+Δφ

当迭代达到稳态时获得尾迹几何收敛解。然后对各尾迹涡元运用Biot-Savart定律计算影响系数。(www.zuozong.com)

线涡元的诱导速度表达式为

其中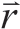为线涡元上的微元到点P的距离，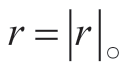

面涡元的诱导速度表达式

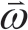为面元环量。

最后计算桨盘上各站点的诱导速度，综合尾迹中所有涡元的贡献，用桨叶上的附着环量乘以相应的影响系数得到：

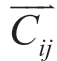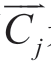其中Гij为第i个径向位置、第j个方位处的附着环量，Гj为第j个方位处的最大附着环量，和是相应的由各涡元引起的影响系数。