振动抑制装置：改进结构抑振系统，降低载荷

任何易振动结构中都可采用一些特殊的动力学修改措施，即采用某种类型的振动抑制装置。通常这些装置是被动式的，需要借助有限的响应来产生反作用力或力矩。这些装置可附加在旋转桨叶和桨毂以及不旋转机体上。此外，可以根据减小幅值（不减小激振力水平）还是减小振源（目的是减小激振力水平）来进行分类。前一种装置的主要特点是必须采用质量元件以“吸收”振动载荷。使用这些质量元件通常要考虑最小化重量要求和最小静变形等基本约束。产生的静变形过大通常是由于根据调谐吸振质量所选择的弹簧刚度较小引起的。稍后将看到，这两种吸振装置间的差别有时是模糊的，这往往取决于在结构减振中我们观测的是响应还是激励。

一、旋翼的相关装置

（一）桨叶摆式吸振器（pendabs）

在旋翼相关装置中，最简单的就是一种摆式吸振器（pendab），它是以简单两自由度吸振器动力学特性为基础的。摆式吸振器基本工作原理是：产生反向动态剪力载荷（在接近共振条件下）以减小传递到桨毂的动态剪力。

附加在旋翼上的摆式吸振器与其他常规吸振器构型的区别是：其刚度几乎全部来自离心力场。因此，它主要调谐在特殊的转速频率下。从图5-3的几何构型图中可以看出这一特点。

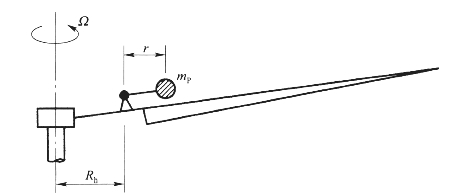
图5-3　典型桨叶摆式吸振器的基本几何构型

利用前面讲述桨叶动力学的概念，可得出摆式吸振器的固有频率ωP，其与摆的质量无关：

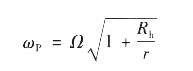
摆式吸振器最主要的作用是：从源头上减小作用在机体上的桨毂垂直载荷。在恰当的调谐条件下，摆式吸振器的响应相位恰好可抵消其连接点外侧桨叶产生的面外振动剪力。摆式吸振器在不同频率下的载荷吸收特性如图5-4所示。

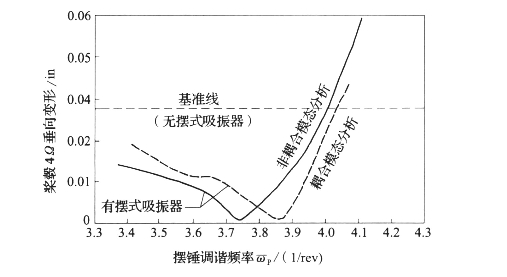
图5-4　桨叶摆式吸振器典型的载荷吸收特性

我们注意到，在调谐频率ωP上，摆式吸振器表现出最佳性能，频率ωP通常稍低于激振力频率，此时桨叶通过频率为从bΩ（b=4）。也应注意当调谐在高于激振力的频率时，摆式吸振器实际上会放大桨毂载荷。

摆式吸振器有以下六个方面的优点。

（1）相对简单，便于分析、设计和安装。

（2）位于桨叶根部，可有效地减小（如果不要求彻底吸收的话）桨毂剪力。

（3）为了有效地吸收桨根剪力而不超出摆的响应范围，摆的质量应做得尽可能大，但是这个非结构质量块降低了旋翼飞行器的有效载荷能力。

（4）摆式吸振器连接铰的阻尼是不可避免的，然而该阻尼对吸振器的工作是不利的。

（5）通常只能减小某一个频率下的垂直桨根剪力。要吸收哪一个谐波频率的奖根剪力，就要为其安装单独的摆式吸振器。

（6）由于直接安装在桨叶上，摆式吸振器的方向会随着桨叶变距角的变化而变化，这种方向变化（通常是不利的）总是会引起吸振器与桨叶面内运动的亲和。

摆式吸振器一个主要缺点是：产生气动阻力，因此会对直升机性能略微产生一些有害影响。

（二）桨毂双线摆吸振器

另一种减小旋翼载荷的被动装置是（面内）双线摆吸振器。该装置与前文提到的用于吸收扭转振动的双线摆吸振器类似。在这里它用于吸收桨毂面内剪力。为了减小固定坐标系中桨叶通过频率bΩ的载荷，双线摆吸振器在旋转坐标中应调谐在（b±1）Ω。例如，针对4片桨叶旋翼，4P的面内桨毂剪力来自3P和5P的旋转桨根剪力，因此需要采用3P和5P两组双线摆吸振器，以吸收4P的不旋转桨毂剪力。从图5-5的几何构型图中，可看出双线摆吸振器与摆式吸振器类似，都调谐在特定的转速倍频上。其固有频率为：

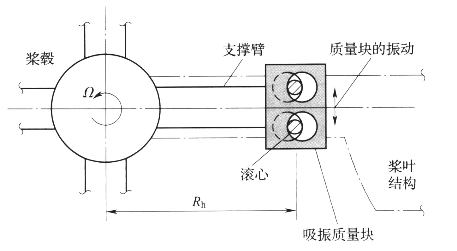
图5-5　旋翼桨毂双线摆吸振器的几何构型

其中，L=（d1-d2），d1和d2分别为双线摆圆孔与滚动支撑销的直径。

桨叶片数±1倍的桨叶面内谐波载荷能够合成面内桨毂剪力，并对机体产生桨叶通过频率（桨叶片数×旋转频率）的激励。为此，两组独立的双线摆吸振器分别调谐在3/rev和5/rev。

双线摆式吸振器的优点如下。

（1）结构简单，其滚动销耐久性好且阻尼较小。安装在桨毂中心，无桨叶连接问题，不会产生与桨叶变距角的耦合。

（2）产生的气动阻力相对于桨叶安装装置更小。

其缺点是：①结构重量较大；②只能间接地减小通过频率的桨毂面内载荷，也就是说，其通常调谐在通过频率±旋翼旋转频率上，因为该频率条件影响着不旋转坐标中通过频率的桨毂载荷。因此，如果双线摆吸振器在旋转系吸收的面内载荷谐波成分对不旋转系通过频率的桨毂载荷分量无贡献，则双线摆吸振器的载荷吸收运动是不起作用的。

（三）桨叶高阶谐波控制

桨叶高阶谐波控制（HHC）相对于前两种装置的区别在于，它是一种主动装置。HHC是一种从源头减小桨叶激振力的装置或系统。该系统的工作依赖于主动的能量源，并依靠计算机来协调几个机构的运动以获得所期望的桨叶变距角的高阶谐波值（通常高于自动倾斜器的1P周期变化）。采用HHC后，桨叶变距角谐波成分中包含了正弦与余弦分量的贡献，其频率分别为nP，（n+1）P，（n-1）P。通常来说，这需要通过液压作动器对自动倾斜器实施nP，（n-1）P和（n+1）P频率的激振才能获得，如图5-6所示。

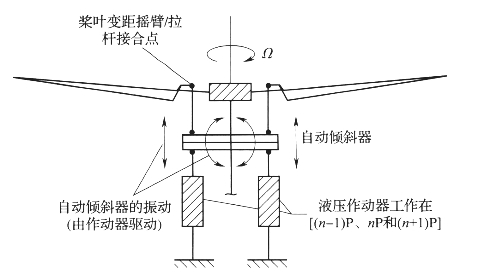
图5-6　HHC系统机械执行机构的基本原理

HHC系统的基本硬件构成是：①一些测试设备（如加速度传感器），以测量机体结构选定位置的振动载荷（load factors）g；②一个机载专用计算机（控制器），用于解析所测量的振动加速度值，并计算出高阶谐波变距控制角6个分量的相应值；③一种执行手段，一般采用液压作动器来执行计算机确定的HHC角度。对于合适的（最佳的）HHC值的计算，可以借助大多数最优控制方法实现。通常采用参数识别方法（如Kalman滤波）计算梯度矩阵，进而建立振动载荷g各个分量相对于HHC变距角6个分量的敏感性。方法原理如图5-7所示。

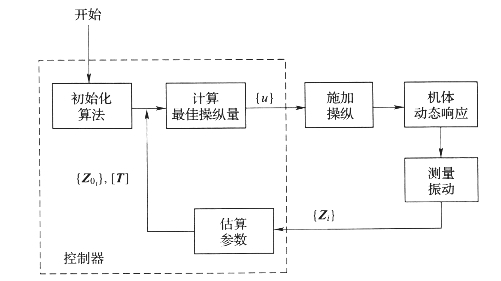
图5-7　高阶谐波控制减振过程的原理示意图

（四）振动测量

除了测量所选机体位置点的全部振动外，还必须采用适当的方法提取出nP的振动成分，包括幅值和相位。提取方法包括许多模拟信号处理方法和数字信号处理方法。

（五）控制器运算

控制器有两个主要功能，其在计算机执行中必须保证足够高的采样率（通常为几次/秒），以确保对振动环境的改变做出准确而快速的响应。第一个功能是，控制器必须进行参数估算，以建立响应矢量和梯度矩阵，这些量将在最优控制过程中用到。特别地，下面的公式定义了执行最佳控制所需的量：其中，{Zi}是测量的振动矢量（即需要最小化的量），{Z0i}是没有HHC控制的{Zi}矢量，[T]是HHC控制角{u}对矢量{Zi}变化的影响系数矩阵，即梯度矩阵。{Z0i}与[T]通常都通过Kalman滤波法得到。

控制器另一个主要功能是计算出最佳的控制量，以最小化由实测振动成分构成的价值函数。必须强调，由于飞行条件的变化和（或）进入机动会引起旋翼飞行器振动环境的持续变化。通常，HHC系统的执行要采用自适应控制算法，以达到最佳的控制设置。对振动水平实施数次/秒的采样，以保证对无控振动水平{Z0i}和梯度矩阵[T]保持精确的更新。这些更新值不断地用于确定新的HHC变距角度，从而使得振动相关的价值函数达到最优值或最小值。

HHC的优点如下：

（1）HHC方法是有效的。试验中已证明其能够有效地持续减小振动。振动主动控制系统的一个优点是，不需要保留振动的一部分残余量来驱动系统工作。

（2）控制器具有通用性，与具体机型的尺寸无关。

（3）HHC系统对于桨叶动应力与气动性能的不利影响是可以忽略的，甚至会产生有益的影响。

然而，HHC也有如下三个缺点。

（1）HHC系统付出了重量代价。如计算机、液压系统与伺服阀以及附加的机体结构强化所产生的额外重量是不可忽略的，在把有效载荷视为首要考虑因素的设计中，重量代价将是决定性因素。

（2）与现有的机体被动减振装置相比，HHC系统更复杂，必须考虑可靠性与维修性。

（3）尽管随着微型计算机的发展计算速度越来越快，但是计算也不是即刻完成的，还是需要一定的运算时间。因此，在一些高频带应用中，HHC系统尚不能很好地跟踪那些随机的或快速变化的振动响应。

随着微型计算机的紧凑性和运算速度不断提高，具有相同运算速度的计算机可以在重量上做得更小，使得HHC方法在重量、可靠性和维修性上变得愈发有竞争力。Wood等人的研究报告中，提出了一种用于OH-6A直升机的HHC原型系统，并在飞行测试中获得成功，有效地减少了振动且并未在桨叶载荷或直升机性能上付出过分代价。是否进行HHC系统的生产性安装，需要在减振收益与附加系统重量和复杂性之间权衡。

二、机体相关的振动抑制装置

与机体连接用于直接减小机体振动的装置，对其有效性的评估都是基于一些基本的动力学考量：尤其是这些装置必须能同时工作在稳态或静载环境以及振动环境中。具体来说，在静载条件下，附加这些装置后的静变形要求小于某些规定值；在振动载荷条件下，要求设备有足够的寿命且轴承的磨损最小等。

（一）传递率

传递率T可作为评价各种减振装置性能的标尺。传递率可定义为：①附加结构的加速度与主结构基础运动加速度的比值；②振动响应幅值与静态（零频）幅值的比值。作为例子，考查一个简单的被动式隔振器。(www.zuozong.com)

（二）简单的被动式隔振器。

简单的被动式隔振器其结构如图5-8所示。

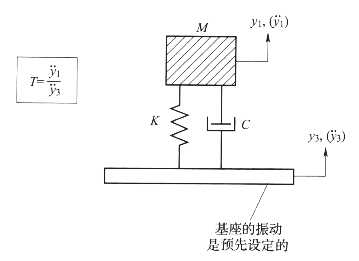
图5-8　简单的被动式隔振器结构图

隔振器传递率随基础运动频率的变化特性如图5-9所示，这里r等于频率比ω/ωn

图5-9　简单被动隔振器传递率的一般特性

从图5-9的传递率结果中可以看出，让隔振器工作在频率比尽可能高于及的范围内是适宜的设计策略。注意，高的频率比意味着低的固有频率ωn。然而，如果隔振器工作在如上图所示的垂直构型系统中，必须考虑由重力W及过载n产生的静变形（下标st）。静变形δst与固有频率的关系可简单表示为

因此，对静变形的限制或成为固有频率选择的一个约束条件，这是依赖频率调谐来减振的设计中必须考虑的。下面，我们再考查一个依赖频率调谐的装置，它具有一些特别吸引人的特性。

（三）动力吸振器

动力吸振器很适合于受外部激振载荷直接作用的系统，如图5-10所示。

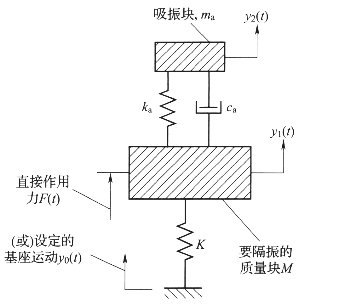
图5-10　动力吸振器示意图

附加质量ma会对作用于主质量M上的外载荷产生响应，这就是两自由度系统（减振设备中的附加质量在机体中容易找到，通常采用航空电池）。一般地，吸振质量连接处包含着黏性阻尼，因此主质量的响应方程（传递率用位移比值定义）为

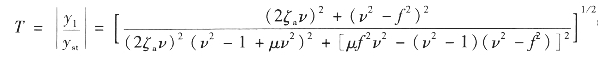
这里，v是激振频率ω与ω0（主质量固有频率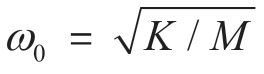的比值；f为ωa（吸振器固有频率）与ω0的比值；µ为两个质量之比（=ma/M）。在实际应用中，激励形式可以是直接的正弦力F或者正弦变化的基础运动位移y0。两种情况下，都需要定义静态变形yst。在基础运动激励情况下，yst即为正弦运动y0的幅值。在施加显式正弦力F情况下，如果通过基础运动施加的激振力幅值为F0，yst可定义为：

附加质量受到外部激振力F（t）作用会产生振动响应，在达到反共振条件下，可将主质量的振动响应减小到接近于0。实际上，当阻尼为0时，公式的分子为0，这就是反共振条件。图5-11给出了典型质量比时的传递率特性。

图5-11　动力吸振器传递率的一般特性

然而，图5-11的结果同时给出了有利的一面和不利的一面。产生反共振最有效的构型是阻尼很小或者无阻尼系统，ζa=ca/cacr。然而，当激励频率等于吸振器固有频率时，附加质量共振产生高响应，而且反共振条件两侧还存在两个共振响应。增加阻尼能够减小这两个共振峰，但代价是也减小了反共振点的效率。

该图也给出了吸振系统另一个有趣的重要性质。图中A点和B点称为不动点，与阻尼大小无关。这些频率位置由频率比f（=ωa/ω0）及质量比µ所决定。Rao的研究指出，这两点ωA/ω0和ωB/ω0的横坐标值（即频率），分别可由以下四次方程的解rA和rB得出：

（四）调谐的吸振器

对于上述两个不动点，其传递率（纵坐标）比频率位置（横坐标）更重要。如图5-11所示，当频率比等于1时，这些传递率值有很大不同。然而，存在某种调谐条件使得两点的传递率相等。该条件定义了一种独特的动力吸振器构型，称为TVA（调谐吸振器）。此时，频率比f与质量比µ的唯一关系为

在公式的调谐条件下，A点和B点的传递率值都为

（五）最佳阻尼

进一步观察图5-11可知，每个固定点都可以选取某一适当的阻尼，以使传递率值最小。因此，对于调谐吸振器，最佳（下标op）阻尼值可在调谐条件限定的传递率范围内找到。对于同一阻尼，尽管两个固定点的传递率限定值不能同时被找到，但可采用平均阻尼值来满足实际的设计需求。

（六）吸振器质量单元的响应

动力吸振器有两种响应情况是设计者所感兴趣的。首先，稳态载荷引起的静变形不能超过某个最大值。对于垂直安装的吸振器，由ωa[=]决定固有频率的同时，都将引起静态垂直变形。其次，第二个感兴趣的响应是，工作中吸振质量与主质量从的运动相互耦合情况。

（七）只带阻尼器的附加质量吸振器

另一种形式的调谐动力吸振器是采用附加质量，但只通过（黏性）阻尼器与主质量相连（这种振动控制装置通常用在其运动轴线方向不含重力分量的情况下）。对于那些由于某些原因常规的调谐构型不宜采用，但是可采用较大的吸振质量而且对减振效果要求不高的情况，通常可以采用这种仅含阻尼支撑质量的吸振器。

（八）节点梁隔振系统（nodamatic isolation system）

另一种隔离机体振动响应的被动措施是使用节点梁隔振系统。首先，将高振动的激振源，如旋翼和减速器连接在一根梁上；然后，将机身连接在该梁的节点上，如图5-12所示。

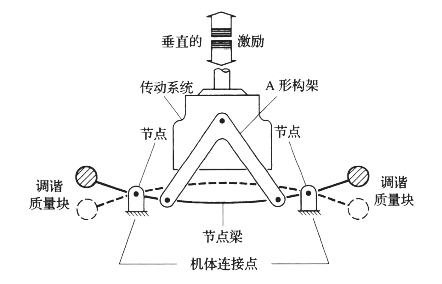
图5-12　节点梁隔振系统示意图

节点梁隔振的原理是：激振载荷在梁节点处（即当梁的弯曲模态接近激振力频率时，在该位置处梁的运动为零）的反作用载荷会得到充分削减。其潜在好处是可以在较大的频率范围内实现减振。尽管节点梁隔振系统简单而且效率相当高，但是其主要缺点是相对较重。

（九）动力反共振隔振器（dynamic antiresonant vibration isolator，DAVI）

那些适合于简单隔振器的情况，动力反共振隔振器（DAVI）也适用。图5-13给出了DAVI的示意图。DAVI的传递率由下式给出：

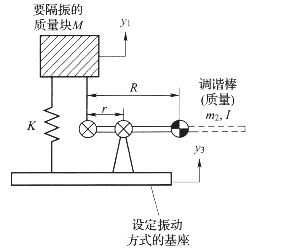
图5-13　动力反共振隔振器运动学示意图

反共振频率WA的表达式为

这里I是含m2元件的支臂相对其质心的质量惯性矩。图5-14是在相同安装条件下，简单隔振器与DAVI的传递率对比，这里静载荷为100lbf，静变形为0.11in，两种隔振器的弹簧刚度是相同的。结果是，DAVI的共振频率总是低于简单隔振器。从两个共振频率之间的某点一直到超出DAVI反共振频率的某点，在这个频率区间内，DAVI的传递率都小于简单隔振器。然而，在更高的频率范围，简单吸振器具有更好的吸振效果。最后指出一点，对于某些构型，DAVI只能在一个非常窄的带宽内调谐到反共振状态，以至于无法使用。尤其是激振力频率发生大范围波动时，更是如此。

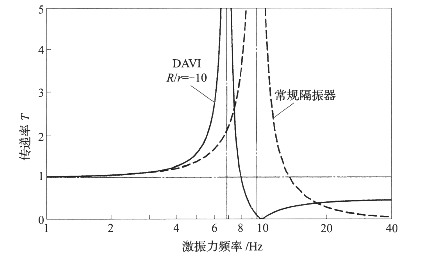
图5-14　简单隔振器与动力反共振隔振器传递率对比

（十）IRIS

改进的旋翼隔振系统（IRIS）是由波音直升机公司研发的一种被动式系统。图5-15是该系统的示意图，从图中可以看出，在某种程度上它是节点梁隔振系统与DAVI的组合。它具有DAVI的反共振特性而且不需要低阻尼轴承，但同样也存在与节点梁隔振系统相关的缺陷，即会带来相当高的重量惩罚。

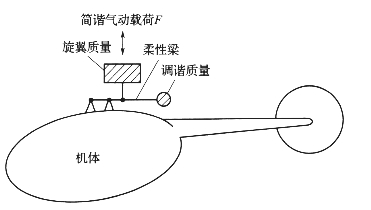
图5-15　lRlS震动隔离装置示意图

（十一）聚焦式隔振系统

前文所讨论的减振装置，其目标大多是减小振动剪力，但聚焦式隔振系统的目标是减小振动力矩。如图5-16所示，该装置采用不平行的连接杆支撑一个惯性体，因此该惯性体的运动被约束在各连接杆的“聚焦”点上。通常，焦点与该惯性体的重心重合，使其起到了“转动”隔振器的作用。与简单的（线运动）被动式隔振器相比，聚焦式隔振器阻尼最小，有更好的性能。

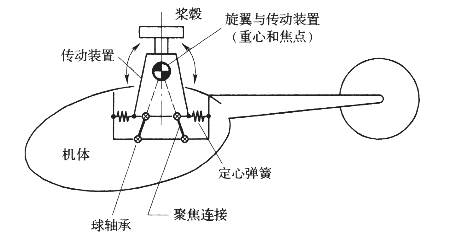
图5-16　聚焦式隔振系统示意图