弹性接触变形分析技术简介

点接触局部共轭齿轮在承载接触时，经过适当跑合后其接触点受载时扩展为接触区，这一点已被广泛应用的圆弧圆柱齿轮所证实。观察跑合后的双圆弧弧齿锥齿轮齿面形貌，其接触区并不是椭圆，而是类似椭圆的香蕉状区域，为了简化计算将之看成长短轴之比比较大的椭圆。采用LTCA 方法时忽略齿面摩擦，齿轮的齿面接触模型如图5−6 所示，齿面接触模型的截面如图 5−7 所示。此齿面接触模型是齿轮在总载荷P 作用下的承载齿面接触模型。在图5−7 中，设在外力作用下，两个齿面有许多对理论接触点位于接触区内。这些理论接触点对可以表示为1−1′、2−2′、…、n−n′，n 是总的理论接触点对数量。εk是理论接触点对k−k′在接触前的齿侧间隙，设 Fk是在总载荷P 的作用下当k 和k′接触时，作用在法线方向的接触力，ωk和ωk′是接触点k 和k′在 Fk作用下的变形，δ0是两个齿面的最小初始间距。假设小齿轮固定，大齿轮轮齿在载荷作用下沿法向的运动量，即轮齿变形后的法向位移为δ。

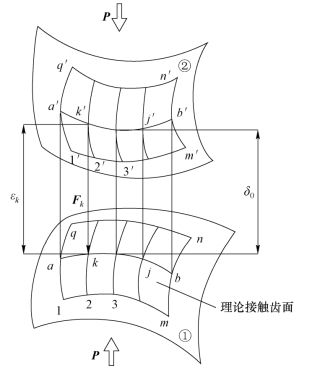
图5−6　齿轮的齿面接触模型

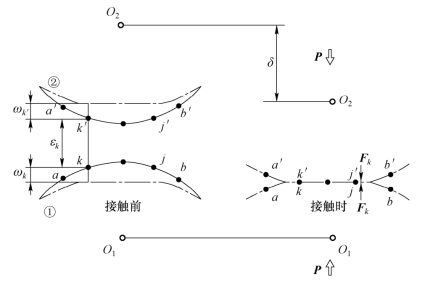
图5−7　齿面接触模型的截面

1）位移协调方程

理论接触点对k−k′接触时ωk+ωk′+εk=δ，即两个点的变形量与初始间隙的和应该等于轮齿变形后的法向位移δ ；而k−k′接触前ωk+ωk′+εk＞δ，即两个点的变形量与初始间隙的和应该大于轮齿变形后的法向位移δ，所以位移协调方程可以写为

即

在采用LTCA 方法时只考虑弹性变形，包括齿面接触变形、轮齿弯曲变形、轮毂扭转变形和支承系统变形，这4 种变形在受载时均出现，但变形程度不同，且接触区变化对4 种变形的敏感程度是不一样的，所以分析载荷对接触区的影响比较困难，需要借助各种理论和手段。利用有限元工具可以探索载荷与变形之间的关系，得出定量关系并应用于LTCA 方法，使分析结果更加符合真实工况。(www.zuozong.com)

2）弹性接触的力平衡方程

本书中假设所有理论接触点的接触力沿着法向总载荷的作用方向，由于接触区域一般比较小，这种假设在工程上是合理的，因此，作用在齿面上的总载荷P 等于各个齿面分布载荷Fj（j=1，2，3，…，n）之和，力平衡方程可以写为

3）数学模型的求解方法

前面的位移协调方程和力平衡方程是判断点是否接触的条件。承载齿面接触问题可以看作是在已知变形影响系数 Skj、初始间距 εk、总载荷P 的条件下，寻找满足上述方程的齿面分布载荷Fj。此时轮齿接触的数学模型为

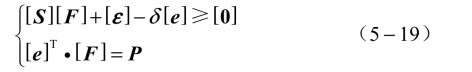
式中　[S]——以变形影响系数 Skj为变量的关系式；

　　　[F]——以齿面分布载荷Fj为变量的关系式；

　　　[ε]——以初始间距εk为变量的关系式。

式（5−19）是一个由已知参数 Skj、εk、P 和未知参数Fj、δ 组成的非线性方程组，目标函数是使变形最小。利用MATLAB 求解非线性方程组可以得出结果。δ 是当前接触位置载荷作用下的线位移传动误差。