多元函数曲线拟合方法：以最小二乘法为例

1.拟合的最小二乘法原理

在科学实验的统计方法中，往往要从一组实验或统计数据中寻找自变量x与因变量y之间的函数关系，即y=f（x），见表5-12。

表5-12 统计实验中的自变量与因变量

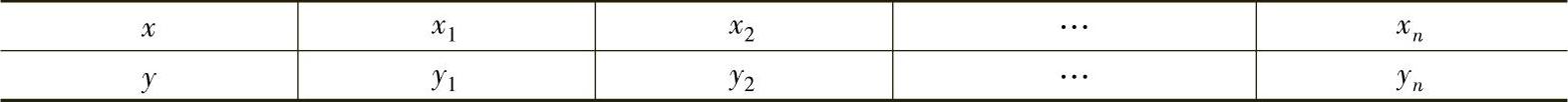
在y=f（x）条件下，对给定的一组数据要求出一个函数y=S^∗（_x），以使误差平方和最小：

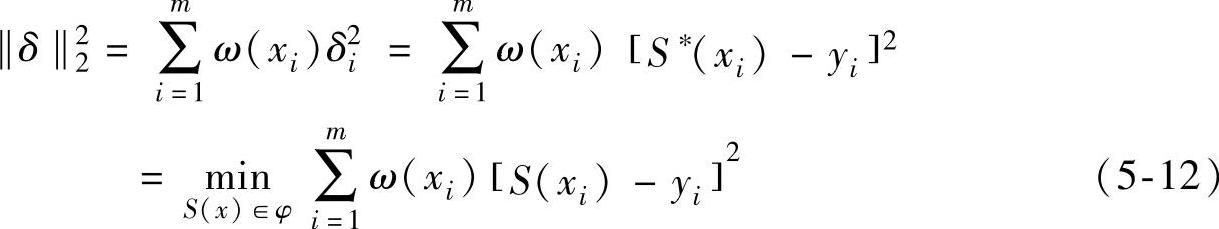
为构造新的函数类型，设函数空间为ϕ=span{1，φ₁（x），φ₂（x），…，φ_n（x）}，则拟合的函数一般形式为S（x）=a₀+a₁φ₁（x）+a₂φ₂（x）+…+a_nφ_n（x）；ω（x_i）≥0为权函数，它表示不同点[x_i，f（x_i）]处不同的数据权重。用最小二乘法求解拟合曲线问题，就是通过在S（x）中求解函数y=S（^∗_x）以使‖δ‖²₂的值最小。这样，问题就转化为求解多元函数极小值（a^∗₀，a^∗₁，…，a^∗_n）的问题。

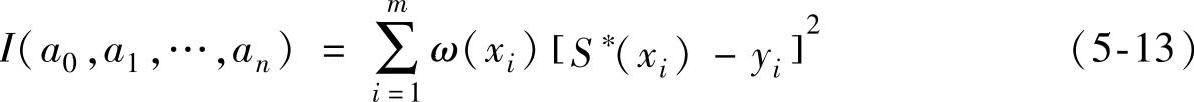
由多元函数极值求解的必要条件，可得

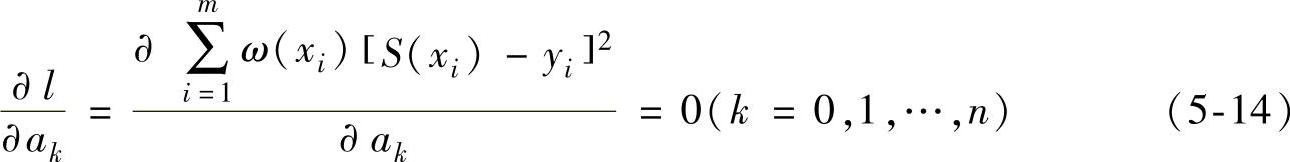
式（5-14）中，y_i是因变量的实验或历史统计数据；S（x_i）是因变量的计算数据。

在不考虑ω（x_i）的情况下将上式展开可得到关于a₀，a₁，a₂…，a_n的方程组：

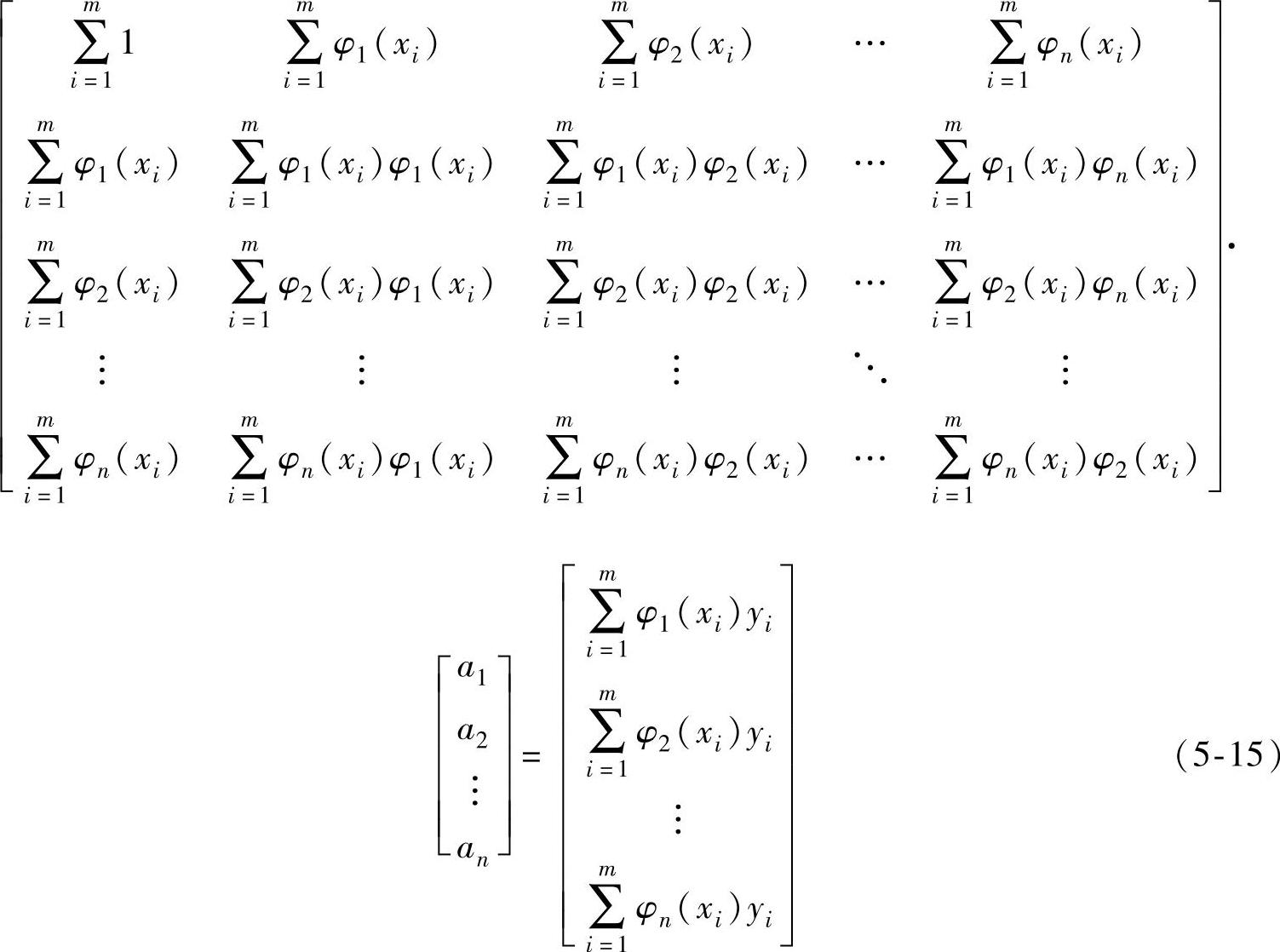
由于φ₁（x），φ₂（x），…φ_n（x）与线性无关，所以方程组存在唯一解：

a_k=a^∗_k（k=0，1，…，n） （5-16）

上述最小二乘法有关概念和方法同样可以推广到多元函数。当n=1时可得一种简单的拟合模型y=a₀+a₁x，其称为线性拟合。这种模型计算简单、应用广泛。

2.曲线拟合法在轴承趋势分析中的应用(www.zuozong.com)

对于滚动轴承而言，磨损是引起轴承失效的主要原因之一，磨损加剧会导致振动加剧。因此，可以以振动幅值为参数，利用最小二乘拟合曲线法进行状态趋势分析来获得轴承的早期预报。表5-13列出了在相同的监测点、间隔相同的时间所获得的振动幅值数据。

表5-13 3月1日至3月10日采集得到的数据

设拟合曲线的方程为y=ax+b，根据最小二乘法求解参数a、b。

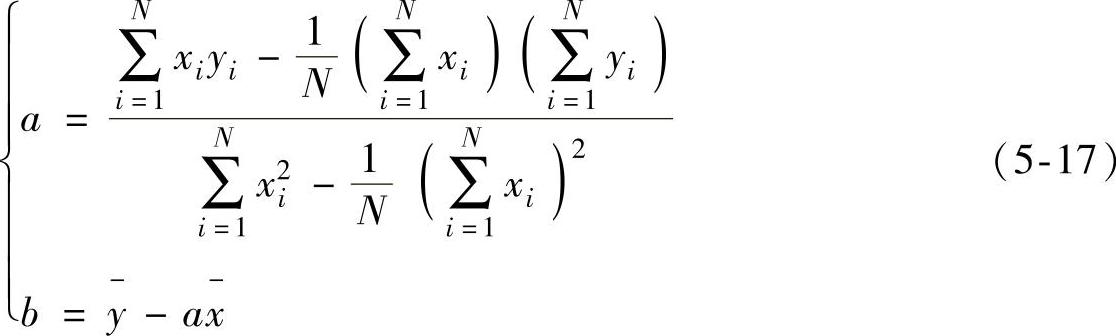
由式（5-15）可得：a=0.1418，b=0.92。因此可以得到直线方程为y=0.1418x+0.92。

为了检验拟合出来的曲线是否可用，还要检验曲线的相关度r，当计算得出的拟合曲线相关度大于等于0.8时，证明相关程度较高，拟合曲线有效；当拟合曲线相关度不足0.8时，则证明拟合曲线不适合于趋势预测。相关度计算公式如式（5-18）所示。

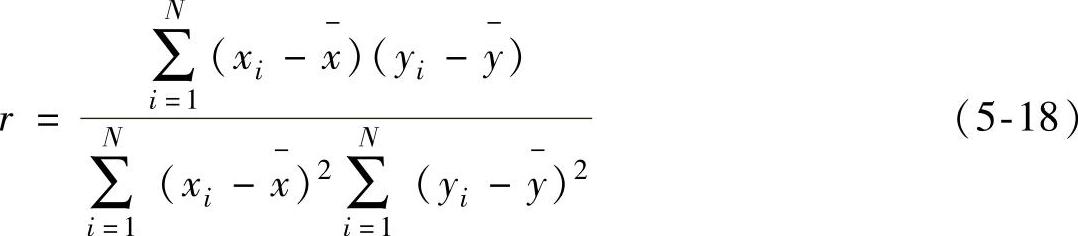
示例中，r=0.96，这说明拟合曲线基本符合线性关系，该拟合曲线可用。

在图中标出采集所得的数据点及拟合曲线，如图5-15所示。

根据具体工况设定报警限值，在本例中假设报警线的上限值达到9mm/s，将已求出的拟合曲线方程和极限值的水平线方程联合求解，即可求出按目前的增长速率达到极限值时的天数。解方程组

可得：x=57天。所求出的x为振幅值达到上限值时的天数，其起始日期为开始测定的日期，预报可连续运转的天数N应扣除测试的天数，本例中：N=57-10=47（天）。

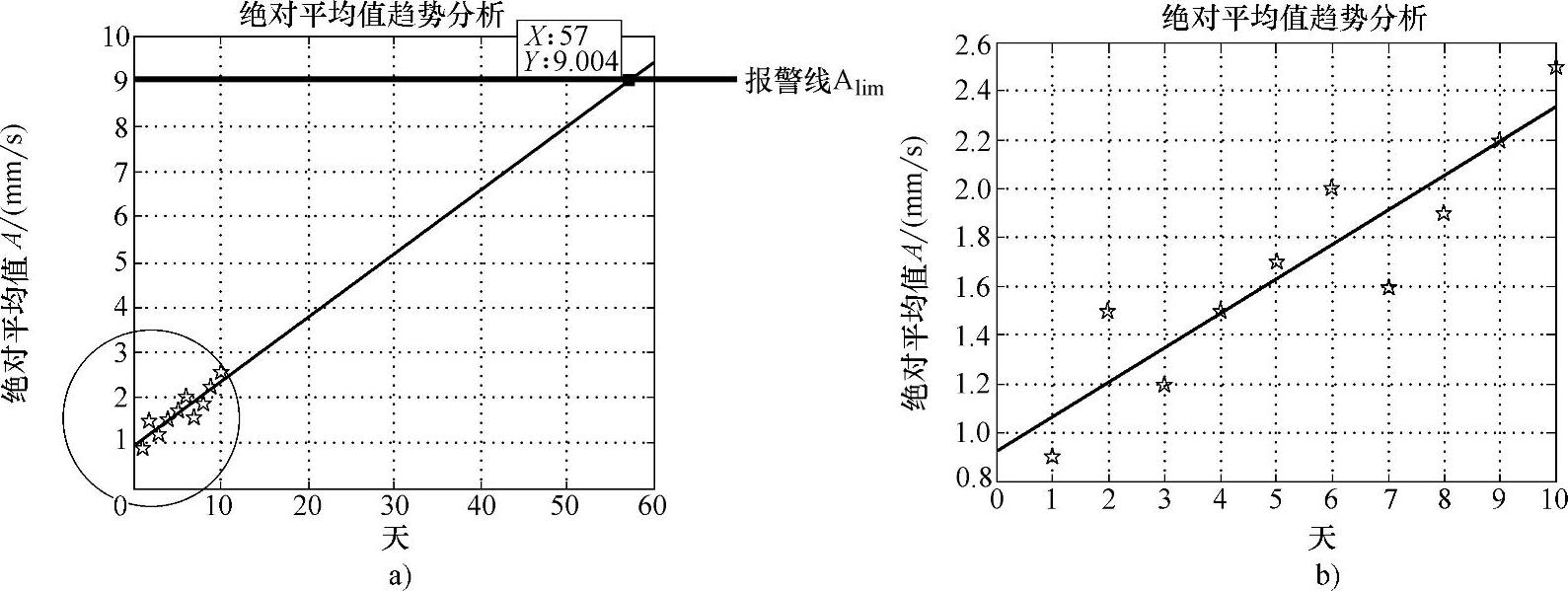
图5-15 采集数据点与拟合曲线

a）趋势分析拟合曲线 b）趋势分析拟合曲线局部放大图