频域分析在故障诊断中的应用

幅域、时域分析所能提供的信息非常有限，往往只是判断滚动轴承是否有故障及故障的严重程度。但是不能说明故障的发生部位，通常只作为设备的简易分析手段。要实现对轴承故障的进一步分析和轴承故障的定位，还需要进行频域分析。

频域分析是把以时间为横坐标的时域信号通过傅里叶变换转化为以频率为横坐标的频域信号。频域分析包括幅值谱、相位谱、功率谱密度、倒频谱等。频域分析主要是分析频谱中的峰值频率与故障频率关系，以此来分析、判断故障的位置。因此在滚动轴承进行分析之前需要了解滚动轴承的各种故障频率及各故障频率之间的关系。

1.滚动轴承的特征频率

当滚动体和滚道接触处遇到一个局部缺陷时，就有一个冲击信号产生。缺陷出现在不同的元件上，接触点经过缺陷的频率是不同的，这个频率就称为冲击的间隔频率或特征频率。

在求特征频率之前，首先要知道各个部件的相对运动的关系。

图3-19 轴承振幅概率密度分布图

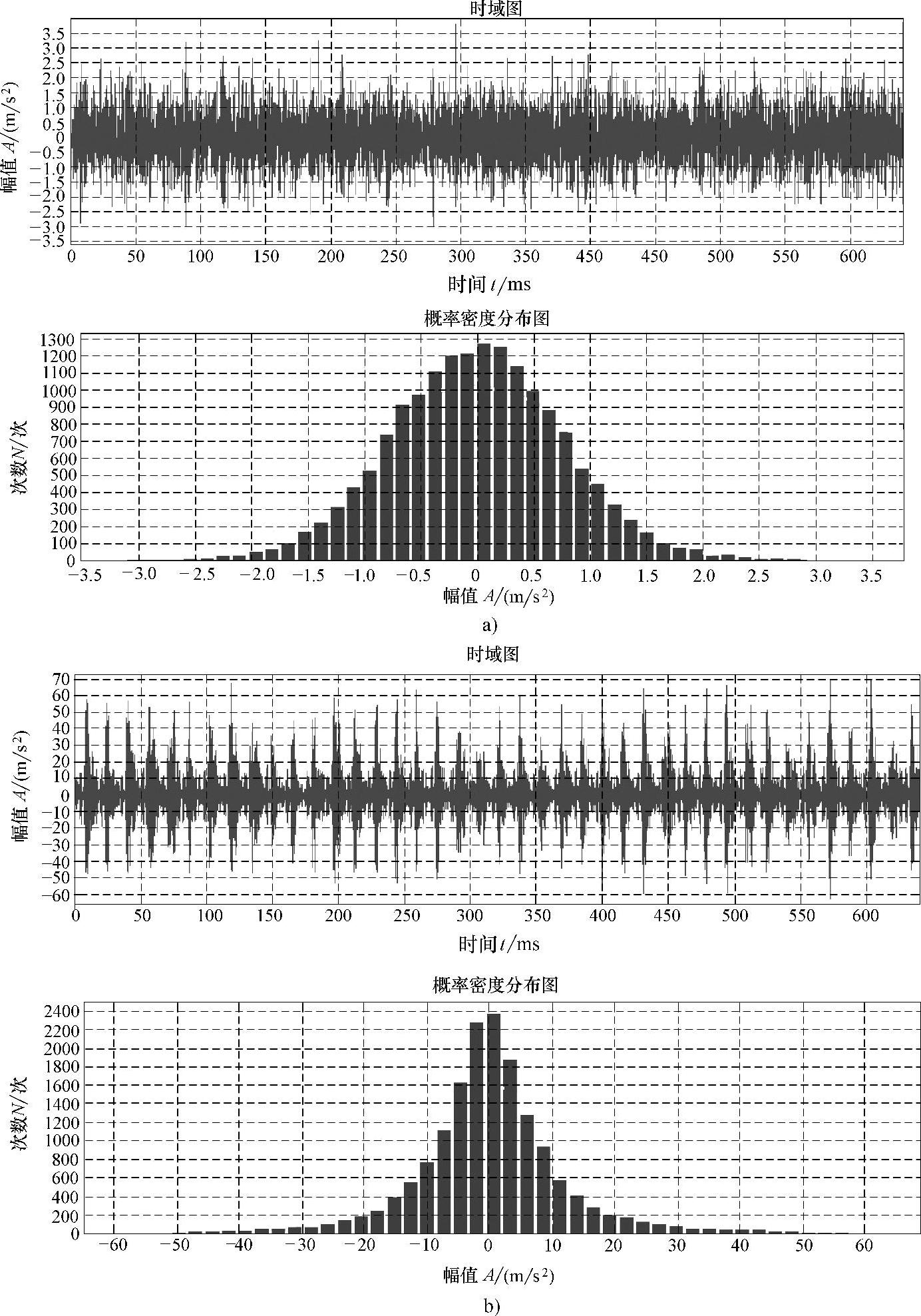
a）正常轴承振幅概率密度分布图 b）外圈故障轴承振幅概率密度分布图

设轴承的内圈和外圈都在转动，在内圈和外圈滚道上分别有接触点A和B，如果径向游隙为零，如图3-20所示，则A点和B点的圆周速度为

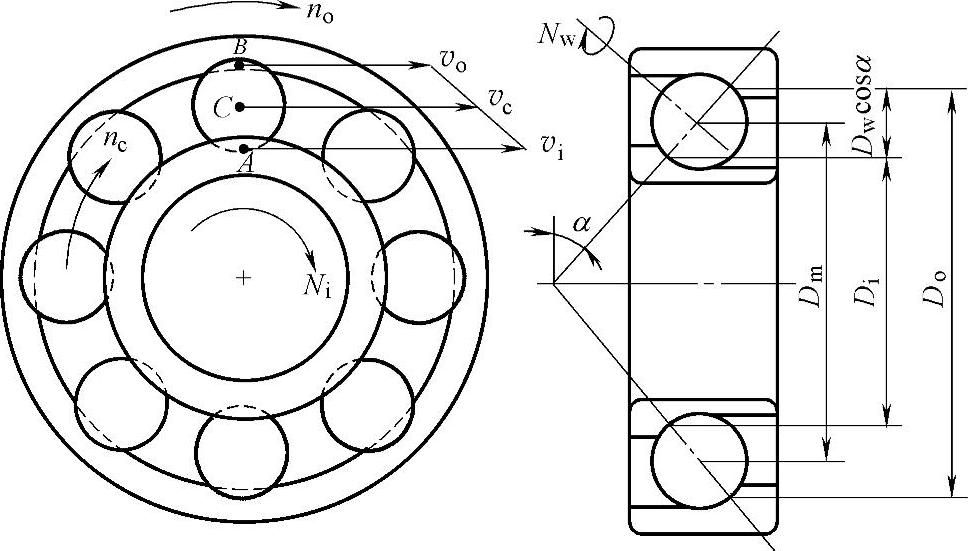
图3-20 轴承各元件之间的运动关系

式中，v_o和v_i分别是外圈、内圈接触点的圆周速度；D_o和D_i分别是外圈、内圈滚道接触点处的直径；n_o和n_i分别是外圈、内圈的转速。

若忽略游隙，由图3-20可知：

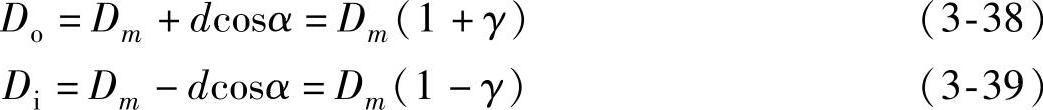
式中，D_m是节径；d是滚动体直径；α是接触角；。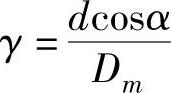

滚动体绕轴承中心公转的速度为v_o和v_i的平均值，即

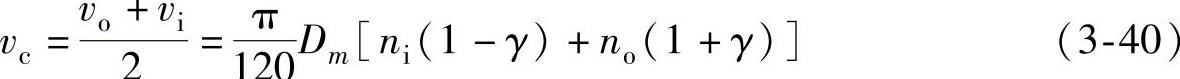
滚动体的公转速度也就是保持架中心圆的线速度。保持架中心圆上某一点的线速度为

根据两种公式，可得保持架的转速：

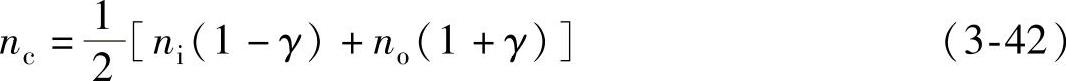
内圈相对于保持架的转速为

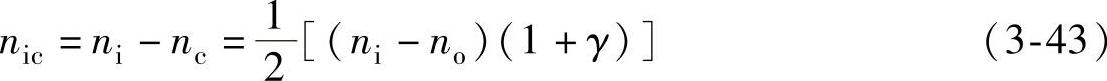
外圈相对于保持架的转速为

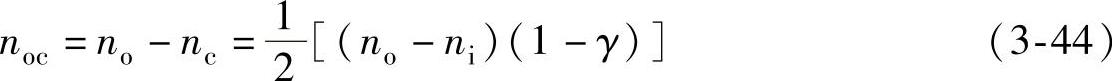
因为接触点处两物体的线速度相等。滚动体上与内圈接触点A的线速度为

内圈滚道上与滚动体接触的A点相对于滚动体中心的线速度为

根据理论力学，相对于保持架建立坐标系。滚动体的运动可分解为公转和自转，公转等于保持架的转速；内圈与保持架同轴转动，在建立的坐标系中滚动体的运动为其自转速度，内圈运动速度为其与保持架的速度差。在新建立的坐标系中两接触点的速度相等，即v_iA=v_oA。

由此可以知道，滚动体的自转速度：

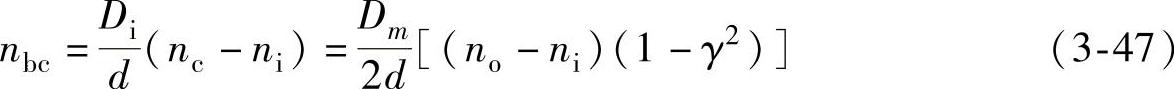
对于绝大多数的滚动轴承在实际的应用中总是保持外圈静止，内圈与轴一起旋转。即n_i=n，n_o=0。因此，内圈相对于保持架的转速为

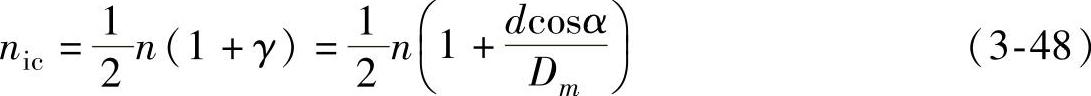
外圈相对于保持架的转速为

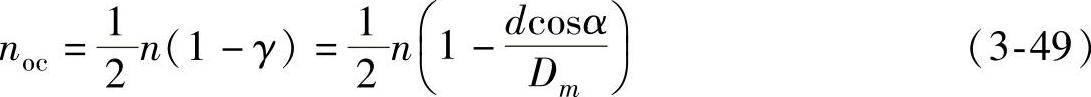
滚动体的自转速度为

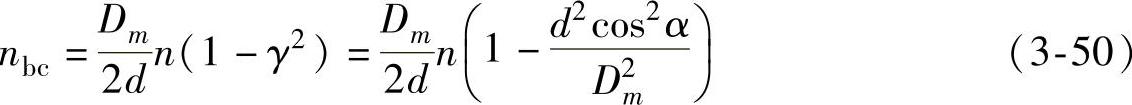
设轴承有z个滚动体，内圈上某一点每分钟通过的滚动体的个数为

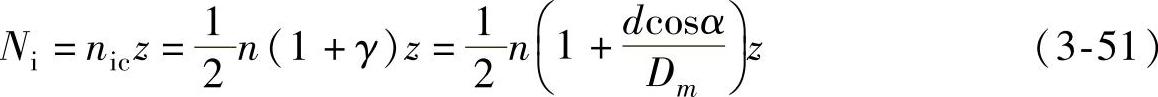
外圈上某一点每分钟通过的滚动体的个数为

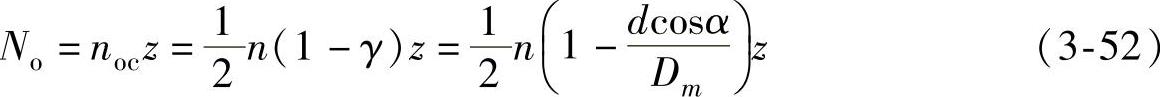
在外圈固定，内圈与轴一起旋转的情况下，若内圈、外圈、滚动体或保持架上有一处局部缺陷，则在缺陷处相接触时便会产生冲击，其频率分别为：

内圈的故障特征频率为

外圈的故障特征频率为

当滚动体上有缺陷时，且滚动体缺陷只冲击单侧滚道时，其特征频率为

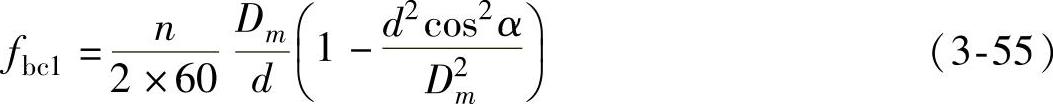
f_bc1即滚动体的自转频率。

当滚动体缺陷冲击双侧滚道时，其特征频率为

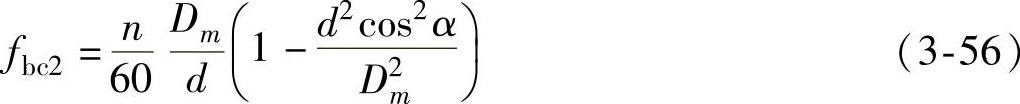
当因保持架变形等因素，保持架与内圈局部接触摩擦，其特征频率为

当因保持架变形等因素，保持架与外圈接触摩擦，其特征频率为

当有多个故障时，特征频率计算公式也是如此。通过以上的公式可以看出各个特征频率有一定的关系：

①外圈故障频率与保持架故障频率间的关系：

f_o=zf_oc （3-59）

②内外圈故障频率之和与转频之间的关系：

f_o+f_i=zf （3-60）

如6207E滚珠轴承，节圆直径D_m=53.5mm，滚珠直径d=11.112mm，滚珠数z=9，轴转速n=1450r/min，压力角α=0°。如果每次只出现一处缺陷，计算该轴承的故障频率如下：

内滚道缺陷：

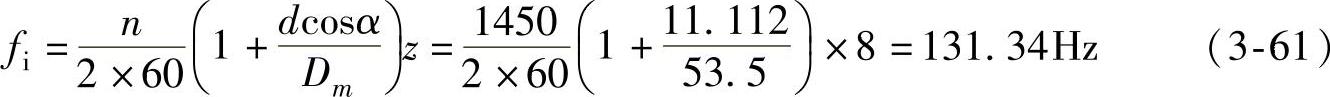
外滚道缺陷：

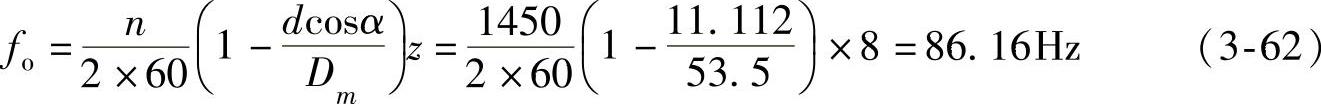
滚珠缺陷：

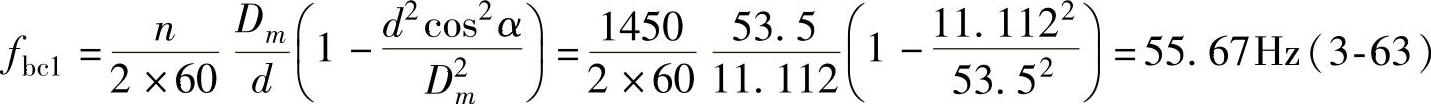
保持架碰外环：

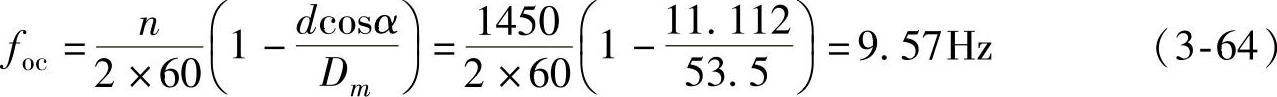
保持架碰内环：(www.zuozong.com)

在实际生产应用中，为了计算的方便也常用如下经验公式：

①保持架的特征频率为f_c=（0.381～0.4）f

②滚动体的自转频率：f_bc1=0.23×z×f（z＜10时），f_bc1=0.18×z×f（z＞10时）

③内圈的故障频率：f_i=0.6×z×f

④外圈的故障频率：f_o=0.4×z×f

进一步深入分析后发现：对于接触角小于45°的推力球轴承，其载荷作用下的接触角要大于无载荷作用时的初始接触角。因此，当接触角发生变化时，理论故障频率的计算值会表现出方向性，结果见表3-6。

表3-6 接触角增大时滚动轴承故障频率的方向性

从上表中可以看出，由于没有考虑载荷作用的影响，使得理论计算出的故障频率与实测计算得到的故障频率会存在偏差。具体表现在：内圈实测故障频率小于理论计算值，而外圈、滚动体、保持架的故障频率都将大于理论计算值。上述分析的结果可为故障诊断分析人员在频谱分析过程中进行故障特征频率辨识时提供参考。

2.滚动轴承的频谱分析

根据滚动轴承的故障形式在频域中表现出的特征，将整个频域分为三个频段，即高频段、中频段和低频段。高频段指频率范围处于2000～5000Hz的频段，主要是轴承固有频率，在轴承故障的早期，高频段反应比较敏感；中频段指频率范围处于800～2000Hz的频段，一般是由于轴承润滑不良而引起碰摩产生的频率范围；低频段指频率范围处于0～800Hz的频段，基本覆盖轴承故障特征频率及其谐波成分。三个频段对应的适用诊断方法见表3-7。

表3-7 不同频段适用诊断方法

（1）幅值谱 对于周期信号，使用傅里叶级数展开的方法可将时域信号转换为频域信号。

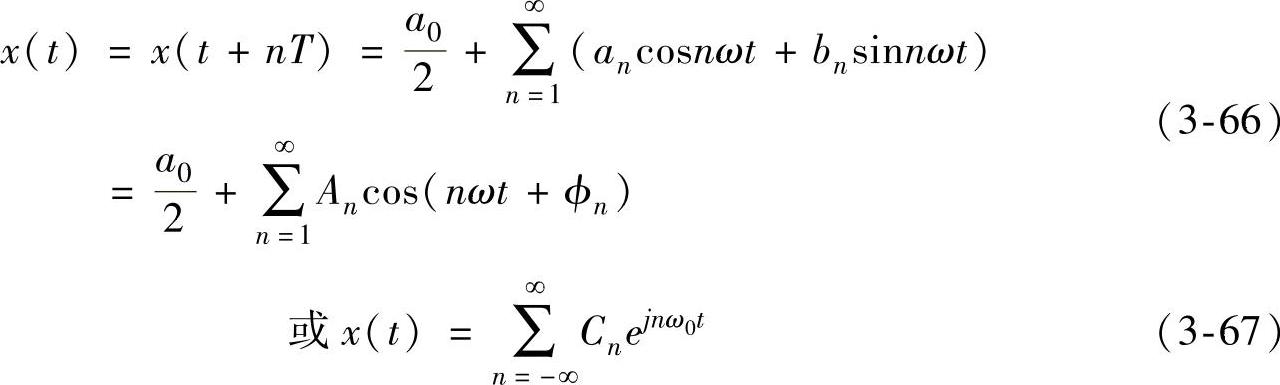
频谱分析是对傅里叶级数展开后的系数进行分析。A_n-ω，C_n-ω的关系就是幅值谱，ϕ_n-ω的关系为相位谱。周期信号的幅值为离散的一条条谱线。

对于时域有限的非周期信号，是通过傅里叶变换的方法转换为频域信号。

幅度谱X（f）的绝对值|X（f）|就是幅值谱。

信号的傅里叶变换X（f）是复数，其可以表示为X（f）=|X（f）|e^iφ（f），其中当φ（f）满足φ（0）=0，且φ（f）在[-π，π]连续时，φ（f）就是x（t）的相位谱。相位谱反映振动组成频率与相位的关系。

在实际工程中，采集的多为离散信号，对于离散信号主要使用Z变换或离散傅里叶变换。离散信号的傅里叶变换表达式如下：

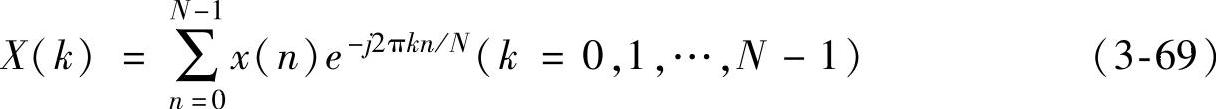
通过对离散信号的傅里叶变换，可以获得信号在频域上的分布特征，进而展开频谱分析，确定轴承的故障位置。

（2）功率谱 功率谱密度函数表示为

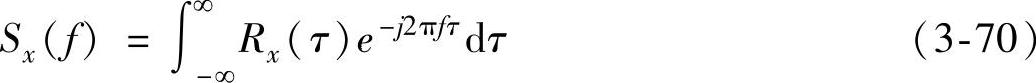
上式中，谱密度函数定义在所有的频域上，称为双边谱。在实际应用中，由于负频率没有实际的物理意义，只对正频率部分进行分析。为保持功率不变，正频率部分的谱值要乘以2倍，称为单边谱密度函数，即G_x（f）=2S_x（f）。

利用功率谱分析滚动轴承的故障，能够更好地凸现轴承的故障频率。如图3-21a所示为某故障轴承振动的原始信号的频谱分析图，图3-21b为功率谱图。从图中可以明显看出：功率谱图更加干净，峰值谱线及其边带谱线也更为明显。对图3-21b图进行局部放大，得到图3-21c，发现在图中的中频区出现共振峰783.2Hz，且两侧出现差值为87Hz的大量边带，这与该轴承的外圈故障频率相吻合。功率谱分析为实现轴承故障的准确诊断提供了有利的分析工具。

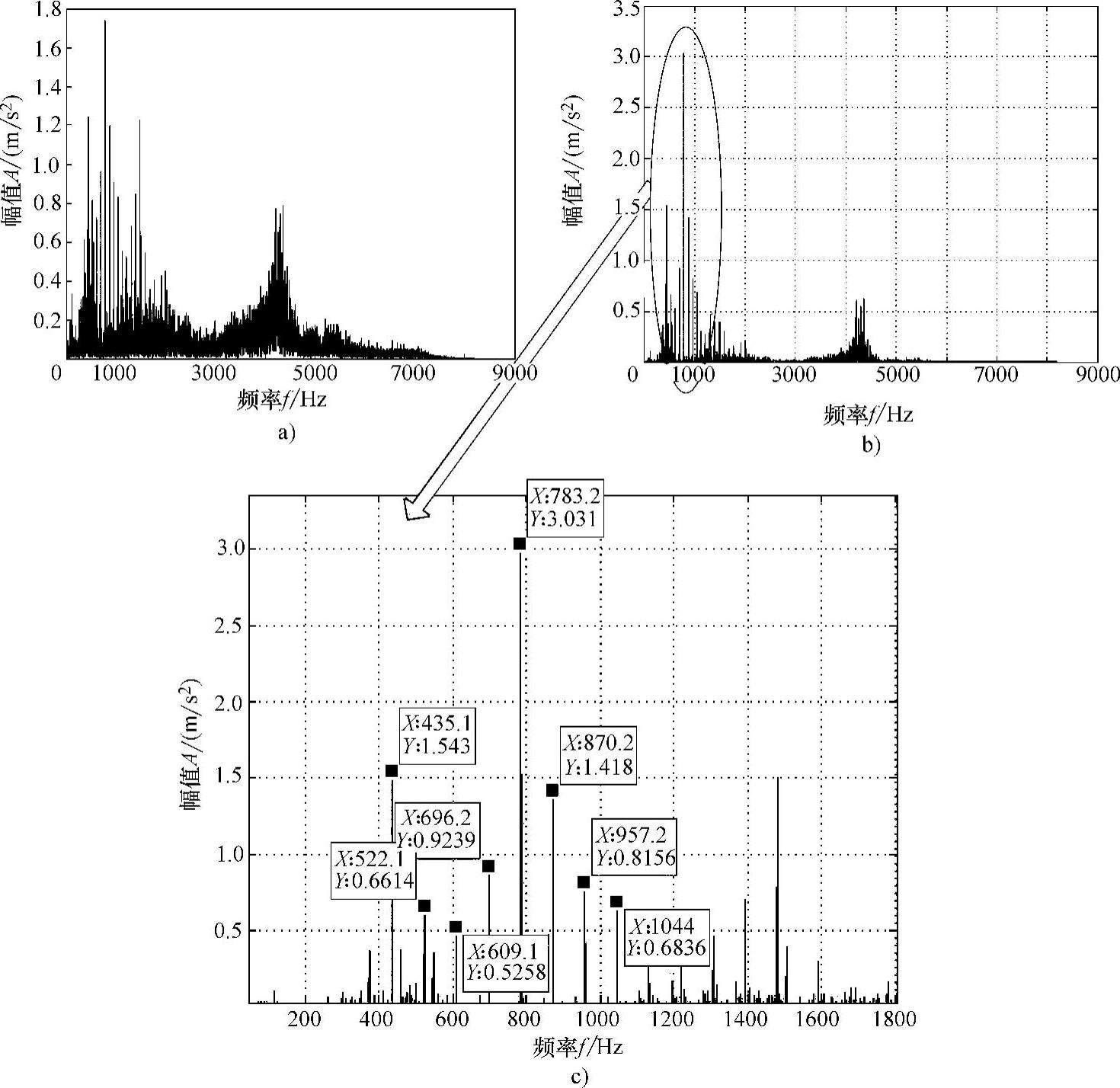
图3-21 故障轴承功率谱分析图

a）故障轴承信号频谱图 b）故障轴承信号功率谱图 c）放大后的功率谱图

（3）倒频谱 倒频谱是对振动信号x（t）的功率谱S_x（f）的对数值进行傅里叶逆变换的结果，倒频谱分为功率倒频谱和振幅倒频谱。工程中常用振幅倒频谱。

功率倒频谱的数学表达式为

C_p（τ）=|F[lgS_x（f）]|² （3-71）

振幅倒频谱的数学表达式为

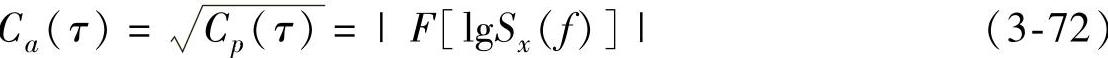
工程实测振动信号、声信号不是振源信号本身，而是振源信号x（t）经过传递系统后的输出信号y（t）。复杂的功率谱为一系列卷积或乘积的形式，通过取对数可转化为简单的求和形式，便于识别信号的主要分量，如图3-22所示是倒频谱对信号的分解过程。这样处理的优点有：将检测信号的功率谱与系统传递函数分离，并将主要的信息从复杂的边频中识别出来。

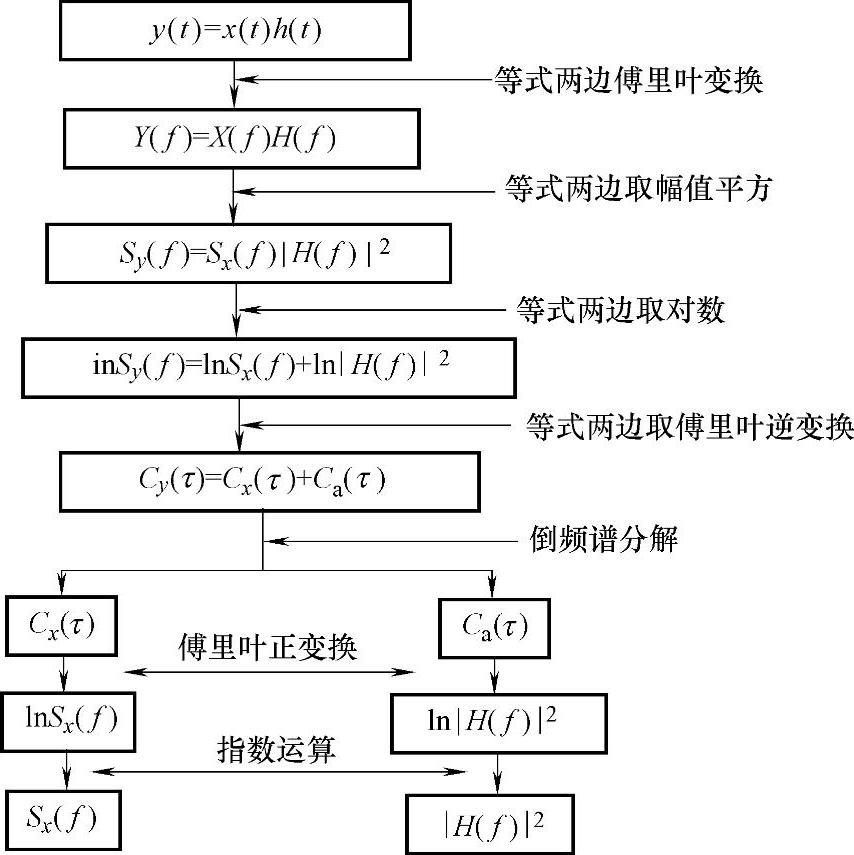
图3-22 利用倒频谱分析信号的基本步骤

在振动信号的检测中由于传感器的安装位置不同，传递途径不同，造成传递函数的差异，使测得的振动信号也会因传感器的安装部位不同而有所不同。更多的情况下，实际工作的轴承安装在设备上，随其运转故障特征会被强背景声淹没，大大降低信噪比，这给基于频谱分析的轴承故障诊断带来了困难。为此，使用倒频谱分析，再配合功率谱做滚动轴承的故障诊断，则更有利于准确提取出轴承故障特征。

倒频谱分析也是通过特征频率来判断故障所在。首先根据轴承的几何参数及转速求得相应的特征频率：内圈特征频率，外圈特征频率，滚动体自转频率，保持架转速频率等。根据倒频谱上最大峰值所在的倒频率，求其倒数就是相应的故障频率。

对某轴承进行故障分析，利用经验公式得到轴承的外圈故障频率为87Hz，内圈故障频率为130.5Hz，保持架故障频率为9.7Hz，滚动体故障频率为50.0Hz。通过计算得到的结果如图3-23所示。图3-23a为故障轴承的时域波形图；图3-23b为进行倒频谱分析的整体效果图，通过整体效果图可以发现倒频谱中存在明显的周期成分；对其进行放大可以得到图3-23c，在倒频谱图中最大峰值处的倒频率为0.01154s，求其倒数得到频率为87Hz。此外，倒频谱上还有一系列其他峰值，其对应的x轴坐标分别为0.02283s、0.0343s、0.04602s、0.06903s……计算可以得到平均周期成分为0.01153s（对应的频率为86.7Hz）的倒谐波，与故障频率进行比较，发现与轴承的外圈故障频率匹配，确定轴承外圈发生故障。

倒频谱分析较功率谱分析的优点在于：利用功率谱分析法诊断滚动轴承故障缺陷时，由于实测功率谱存在着大量非对称分布的边频，给故障部位的确定带来困扰，而倒频谱计算中实质起到信号的解调作用，因此借助倒频谱则能将其化作单根的倒频谱线来进行分析。另外，实测功率谱会因传感器安装部位的不同而变化，而这些变化反映在倒频谱上，只表现为一些十分低缓的随机分量。倒频谱的这种分离特性，对于在复杂的干扰背景下获取有用信息非常有效。

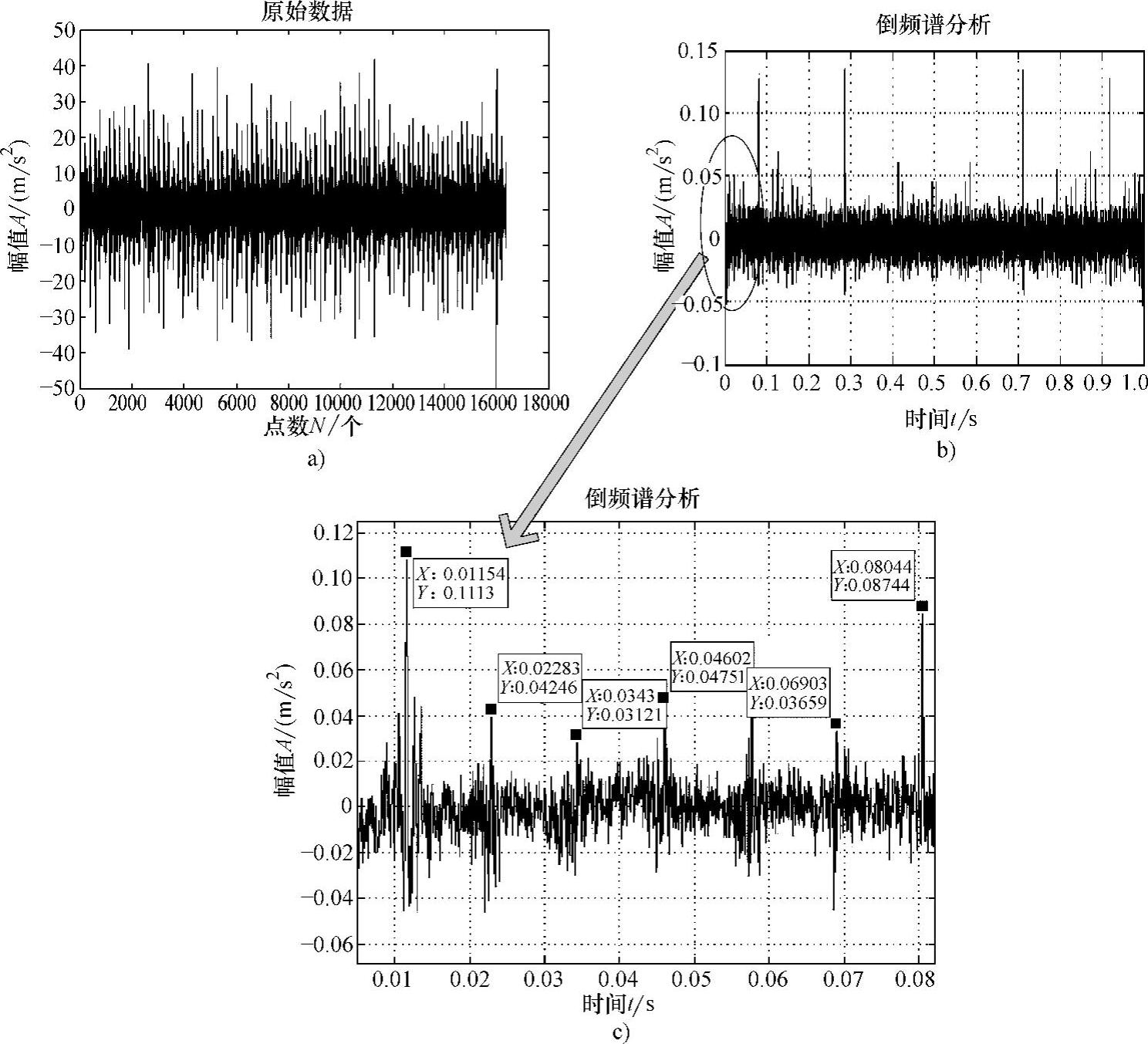
图3-23 故障轴承的倒频谱分析图

a）故障轴承的时域波形图 b）倒频谱分析得到的图谱 c）放大后的倒频谱图

3.频域的有量纲参数

在对频谱进行分析的过程中，除了进行谱图分析外，与时域分析是类似的，也存在频谱的有量纲参数，主要包括频率重心、频率均方、频率均方根、频率方差、频率标准差等。各参数的连续函数式和离散式的计算公式分别如下所示。

（1）频率重心FC：

（2）频率均方MSF：

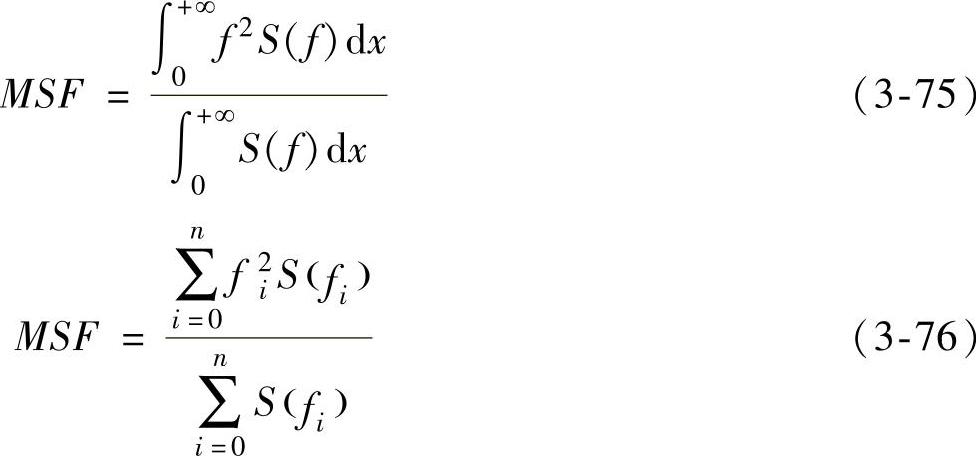
（3）频率均方根RMSF：

（4）频率方差VF：

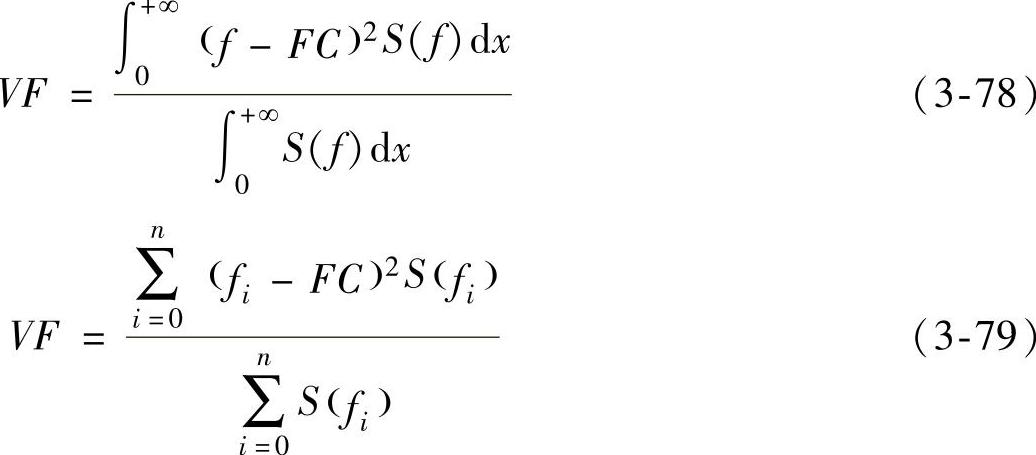
（5）频率标准差RVF：

以上各公式中的S（f）均为信号的功率谱，其中频率重心FC、频率均方MSF和频率均方根RMSF都是用来描述功率谱主频带的位置变化，而频率方差VF和频率标准差RNF则用来描述谱能量的分散度。

从物理意义上看，若把功率谱S（f）看作是横放在坐标轴上的一根杆的质量密度函数，则FC是该杆的重心横坐标值，当靠近原点处的密度较大时[即S（f）的低频谱值较大]，重心将靠近原点，FC值较小；反之，重心将远离原点。RMSF是该杆绕原点的回转半径，当靠近原点的密度较大时，回转半径较小，RMSF值也较小；反之回转半径较大。而RVF是该杆绕重心的回转半径，当S（f）靠近重心处较大时，RVF值较小；反之，RVF值较大。

从数学意义上看，FC、MSF、和VF都是S（f）的加权平均和，它们的权函数均为S（f），只是权不一样，FC的权是f，一个线性权，MSF的权为f²，是平方权，而VF的权为（f-FC）²。

利用频域参数指标可以对滚动轴承的故障进行粗略的判断。当轴承无故障时，频率成分主要集中在低频，FC较小；出现局部损伤类故障时，由于冲击引起的共振，所以主频区右移，FC增加。

4.频域的无量纲参数

与时域类似，在频域中也存在无量纲的参数。利用通频值（故障频率及其倍频对应的幅值之和）与转频的幅值进行比较，通过比值关系来判断故障程度。利用图3-11提到的轴承试验台验证频域无量纲参数的有效性，结果见表3-8。

表3-8 不同故障等级的轴承的频域无量纲参数结果比较

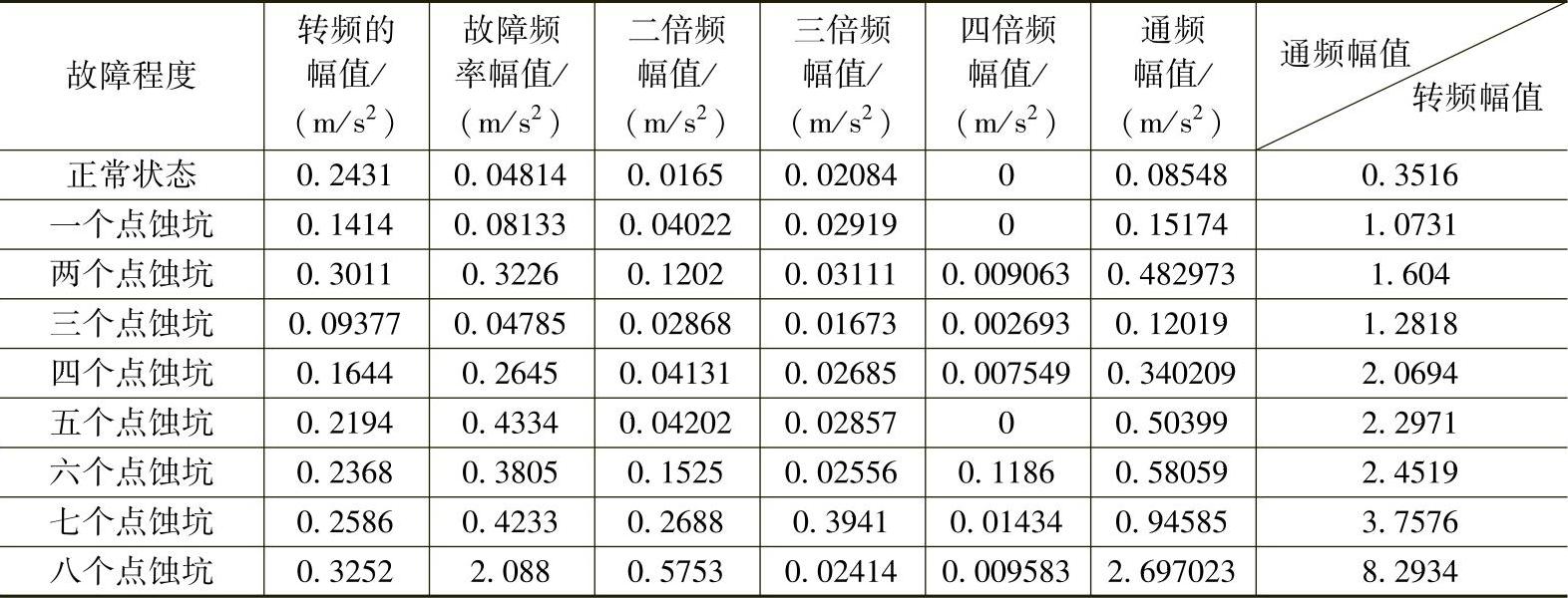
通过统计分析，发现随着故障程度的加剧，通频幅值与转频幅值之比逐渐增大，如图3-24（横坐标为轴承外圈上的点蚀坑个数）所示，通过使用转频幅值作为比较的基准，可以消除外界干扰，把故障引起的频率特征幅值与转频幅值直接关联起来，通过观察通频幅值与转频幅值之比的变化情况，可判断故障的程度及轴承的劣化趋势。

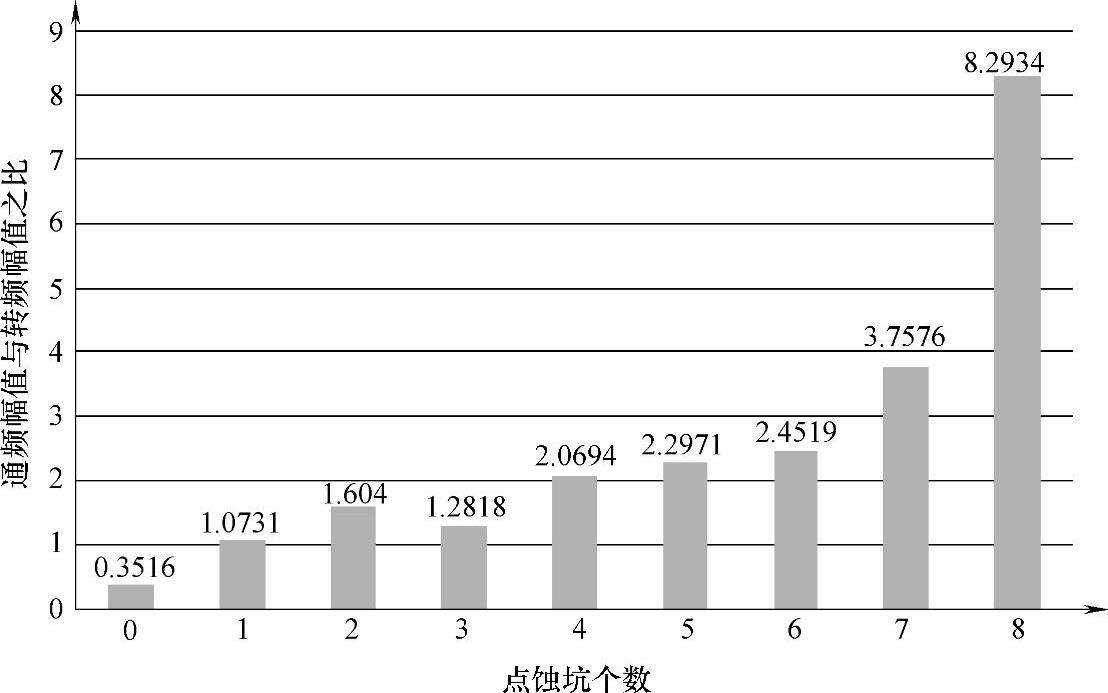
图3-24 频域无量纲参数的应用