如何计算两端铰支细长压杆的临界荷载？

两端为铰支的细长压杆,如图8-2所示。取图示坐标系,并假设压杆在临界荷载作用下,在xOy 平面内处于微弯平衡状态。

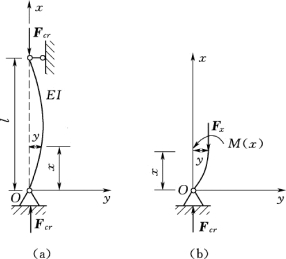
图8-2

其任一截面上的弯矩为

式中：y 为x 截面处的挠度。

应用梁的挠曲线近似微分方程

将式(8-1)代入式(8-2),得

若令

则式(8-3)可写为

(www.zuozong.com)

这是一个二阶齐次常微分方程,通解为

式中的待定常数A、B 和k 可由杆的边界条件确定。对于两端铰支压杆,边界条件为

将此边界条件代入式(8-6),得

式中A≠0,否则,y＝0,即压杆各点处的挠度均为零,这显然与杆微弯的状态不相符。因此,只可能是sinkl＝0,即kl＝nπ/l或k＝nπ/l,其中n＝0,1,2,3,…

将k＝nπ/l代入式(8-4),得

由压杆处于微弯状态平衡的假设及临界压力Fcr应为不稳定平衡时所受的最小轴向压力,因此取n＝1。由此得两端铰支细长压杆的临界荷载为

式(8-7)又称为欧拉公式。

应当注意的是,在两端支承各方向相同时,杆的弯曲必然发生在抗弯能力最小的平面内,所以式(8-7)中的惯性矩I应为压杆横截面的最小惯性矩；杆端各方向支承情况不同时,应分别计算,然后取其最小者作为压杆的临界荷载。