物体重心的坐标公式及应用

(一)重心坐标的一般公式

设一物体重心为C,在如图5-1所示坐标系中的坐标为(xC,yC,zC),物体的重度为γ,总体积为V。假想把物体分割成许多微小体积ΔVi,每个微小体积所受的重力为ΔFGi＝γΔVi,其作用点坐标为(xi,yi,zi)。整个物体所受的重力为FG＝∑ΔFGi。应用合力矩定理可以推导出物体重心的近似公式：

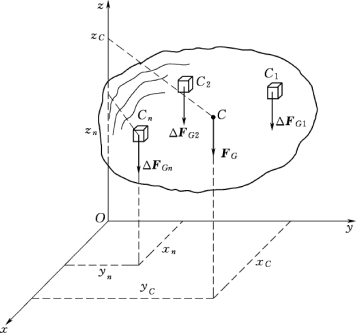
图5-1

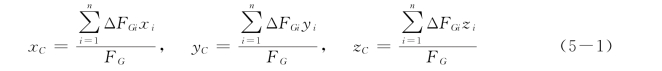
微小体积ΔVi 分割越小,重心位置越精确,在极限情况下便得到物体重心的一般公式：

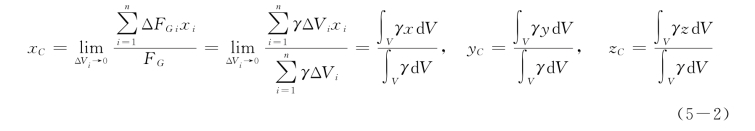
(二)均质物体重心(形心)坐标公式

对于均质物体(常把同一材料制成的物体称为均质物体,其γ 为常量),式 (5-2)变为

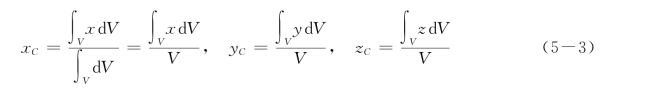
式(5-3)表明,对均质物体而言,物体的重心只与物体形状、尺寸有关,而与物体的重量无关,由物体的几何形状和尺寸所决定的物体的几何中心称为物体的形心。可见,均质物体的重心与其形心重合。重心是物理概念,形心是几何概念。(www.zuozong.com)

(三)均质薄壳重心(形心)坐标公式

由于薄壳的厚度远小于其他两个方向尺寸,可忽略厚度不计,故形心公式为

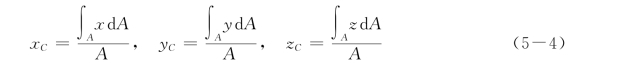
式中：A 为薄壳的总面积。

对于平板(或平面图形),如取平板所在的平面为xOy 坐标平面,则zC＝0,xC、yC由式(5-4)中的前两式求得。

(四)均质杆重心(形心)坐标公式

对于均质细杆(或曲线),可以得到相应的坐标公式为

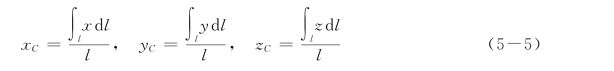
式中：l为细杆的总长度。

对于平面曲线,取曲线所在平面为xOy,则zC＝0,xC、yC 由式 (5-5)中的前两式求得。