如图3-15 (a)所示,简支梁AB 在荷载F 和支座反力FA、FB 的共同作用下处于平衡状态,用截面法分析截面n-n上的内力。
(1)假想用截面n-n将梁分为两段。
(2)取左段为研究对象[图3-15 (b)]。舍弃部分对保留部分的作用用截面上的内力代替,则内力与外力FA 平衡。显然,FA 有使左梁段上下移动和绕截面形心O 转动的作用,因而截面上相应有与之平衡的两种内力Q、M。
剪力Q——限制梁段沿截面方向移动的内力,单位为N 或kN。
弯矩M——限制梁段绕截面形心O 转动的内力矩,单位为N·m 或kN·m。
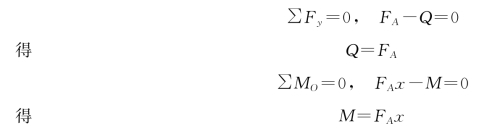
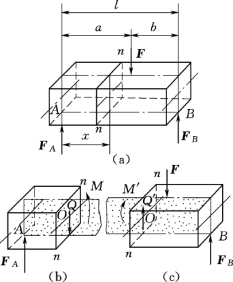
图3-15
(3)由梁段的平衡条件若研究右梁段的平衡,可得同样结果,如图3-15 (c)所示。
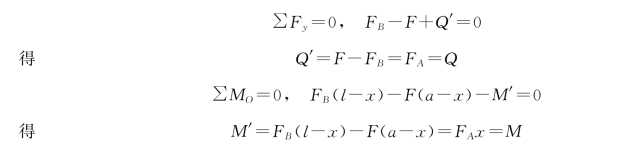
为了取不同的研究对象计算同一截面的内力时数值和符号均相同,梁的内力符号规定为：
剪力Q：使截面邻近的微梁段有顺时针转动趋势的剪力为正值,反之为负值[图3-16 (a)]。
弯矩M：使截面邻近的微梁段产生下边凸出,上边凹进变形的弯矩为正值,反之为负值[图3-16 (b)]。
【例3-4】 已知简支梁AB 如图3-17 (a)所示。求距左端支座2m 处截面上的内力。已知F1 ＝20kN,F2＝40kN。
图3-16
解：(1)求支座反力。由整体的平衡条件得
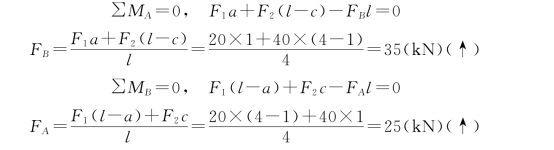
(2)用截面法求内力。截取截面左段梁为研究对象,画受力图如图3-17 (b)所示,为便于判断计算结果,图中未知内力都按符号规定的正向假设。由左段梁平衡条件得
计算结果均为正值,实际内力方向如图3-17 (b)、(c)所示。
由以上计算结果可见,由梁上外力可直接计算截面上的内力。
(1)梁任一横截面上的剪力,在数值上等于该截面一侧梁段上所有外力在截面上投影的代数和,即Q＝∑FiQ。
(2)梁任一横截面上的弯矩,在数值上等于该截面一侧梁段上所有外力对截面形心力矩的代数和,即M＝∑MO(FiQ)。
由外力直接判断内力符号的方法如下：
(1)对截面产生顺时针转动趋势的外力 (截面左侧梁上所有向上的外力或截面右侧梁上所有向下的外力)在截面上产生正剪力；反之产生负剪力,如图3-18 (a)所示。
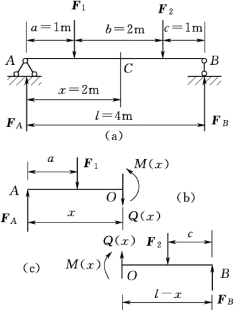
图3-17
图3-18
(2)使梁段产生下边凸出、上边凹进变形的外力(截面两侧梁上均为向上的外力,使梁产生左侧截面顺时针、右侧截面逆时针的外力矩)在截面上产生正弯矩；反之产生负弯矩,如图3-18 (b)所示。
直接由外力计算截面内力时,先看截面一侧有几个外力,再由各外力方向判断产生内力的符号,最后计算各项代数和确定截面内力。
【例3-5】 简支梁上作用集中力F＝1kN,集中力偶m ＝4kN·m,均布荷载q＝10kN/m,如图3-19所示。试求截面1-1和截面2-2上的剪力和弯矩。
解：(1)求支座反力。由整体的平衡条件,可得
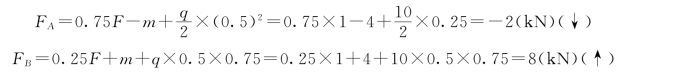(www.zuozong.com)
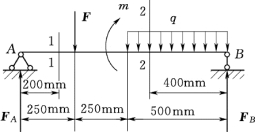
图3-19
(2)求内力。
截面1-1左侧外力为
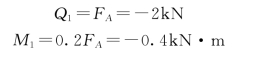
截面2-2右侧外力为
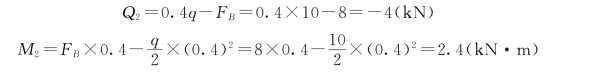
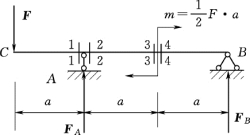
图3-20
【例3-6】 外伸梁受荷载作用如图3-20 所示。图中截面1-1、截面2-2 分别无限接近于截面A 的左侧、右侧,截面3-3、截面4-4 分别无限接近于跨中截面的左侧、右侧。试求图示各截面的剪力和弯矩。
解：(1)求支座反力。取整体为研究对象,由
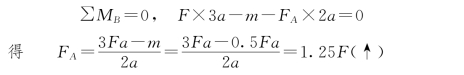
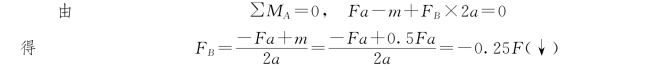
校核：∑Fy＝FA＋FB-F＝1.25F-0.25F-F＝0,计算无误。
(2)计算指定截面的剪力和弯矩。由截面左侧梁段上外力计算：
截面1-1Q1＝-F, M1＝-Fa
截面2-2Q2＝FA-F＝0.25F, M2＝-Fa
由截面右侧梁段上外力计算：
截面3-3Q3＝-FB＝0.25F, M3＝-m＋FBa＝-0.75Fa
截面4-4Q4＝-FB＝0.25F, M4＝FB·a＝-0.25Fa
比较截面1-1、截面2-2的内力：
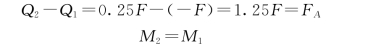
可见,在集中力左右两侧截面上,弯矩相同,剪力发生突变,突变值等于该集中力值。
比较截面3-3、截面4-4的内力：
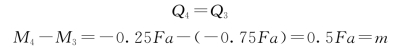
可见,在集中力偶左右两侧横截面上,剪力相同,弯矩发生突变,突变值等于该集中力偶的力偶矩。
由此可知,计算集中力和集中力偶作用截面的内力时,须分别计算该截面两侧相邻截面的内力。
【例3-7】 试求图3-21所示外伸梁C、A、E、B、G 各截面上的内力。已知F＝3kN,q＝1kN/m,m＝6kN·m。
解：(1)求支座反力。
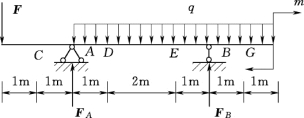
图3-21
校核：∑Fy＝FA＋FB-F-q×6＝4.5＋4.5-2-1×6＝0,计算无误。
(2)计算各截面内力。
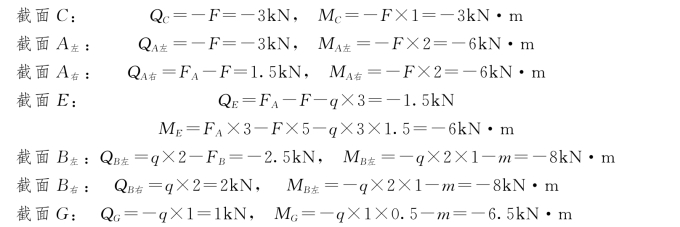
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
