
实际运算放大器的参数总不能达到理想境界,所以分析由于实际放大器各项参数的非理想性所造成的运算误差很有必要。下面的分析假设运算放大器是线性元器件,可以采用叠加原理,在分析某种原因造成的误差时,先假设其他参数是理想的,然后用叠加原理得到综合误差。
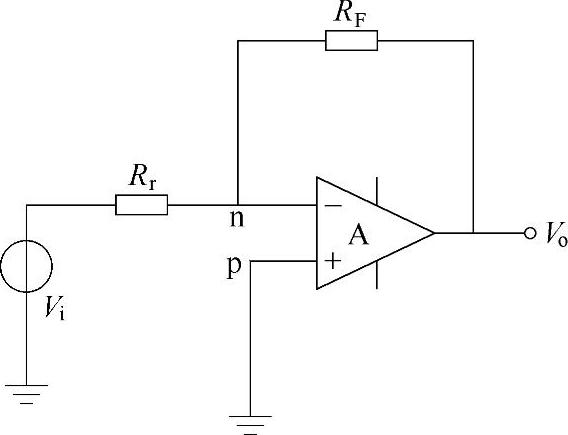
图2-4 反相输入放大器电路
1.开环电压增益的影响
在分析放大器的开环增益有限时的误差,可先假设放大器的输入阻抗为无穷大,只讨论开环增益有限时对闭环增益的影响。
(1)反相输入放大器 当放大器的开环增益有限时,图2-4中n点的电位不再是零,而是
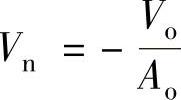
假设放大器的输入阻抗为无穷大,即流过Rr与RF上的电流相等,则

解得闭环增益为
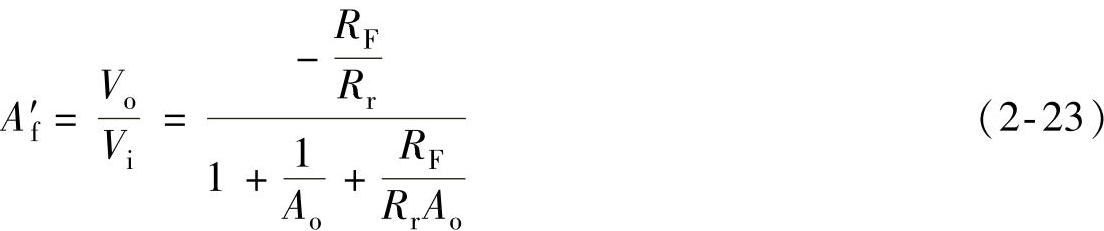
令

LG叫做环增益,则

式(2-25)中的分子部分正是理想放大器的反相输入闭环增益,所以式(2-25)也可写成:

当开环增益Ao→∞时,LG→∞,则实际增益A′f等于理想增益Af。
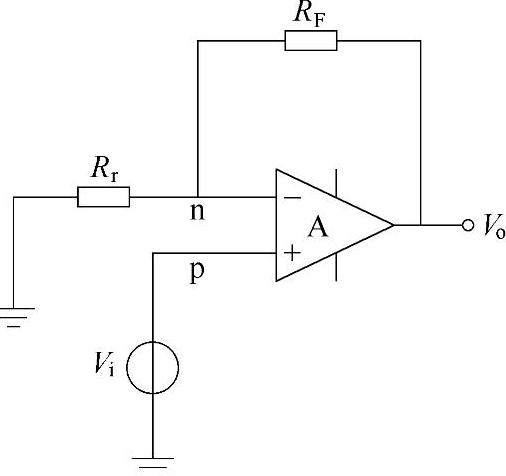
图2-5 同相输入放大器电路
(2)同相输入放大器 同相输入放大器如图2-5所示。如果放大器的开环增益为有限值,则由
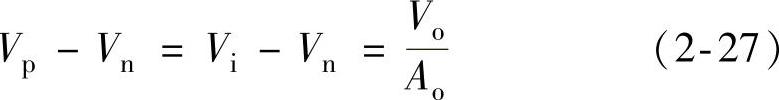
可得

设放大器的输入阻抗为无穷大,即流过Rr与RF的电流相等,则

将式(2-28)代入式(2-29)中,经过整理得到同相输入时的闭环增益为
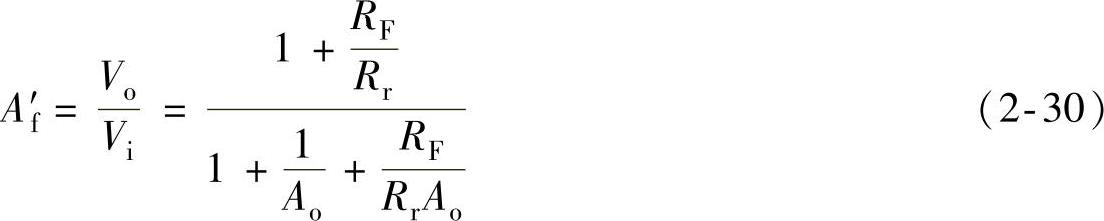
或者

即当开环增益不是无限大时,闭环增益A′f不再等于理想增益。换句话说,在这种情况下用理想运算放大器的闭环增益公式就会有一定的误差。
式(2-26)与式(2-31)形式完全相同,如果令实际增益与理想增益的相对误差为δ,则由此二式知
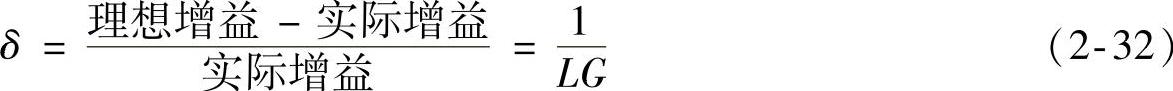
这表明,由开环增益有限引进的误差对同相输入放大器与反相输入放大器都等于环增益的倒数。由式(2-24)知,环增益不但与放大器的开环增益有关,还与外接反馈电阻有关。开环增益越大,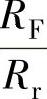 越小,误差也越小。例如,当开环增益为100dB,闭环增益为40dB时,增益误差为0.1%。如果闭环增益达到60dB(1000倍),则增益误差可达到1%。由此可见,若闭环增益高,则要求放大器的开环增益也要高。
越小,误差也越小。例如,当开环增益为100dB,闭环增益为40dB时,增益误差为0.1%。如果闭环增益达到60dB(1000倍),则增益误差可达到1%。由此可见,若闭环增益高,则要求放大器的开环增益也要高。
2.输入失调电压的影响
由式(2-1)知,当理想运算放大器的输入信号为零时,其输出电压也是零。但是对实际运算放大器,由于其输入失调电压不是零,并不满足零输入时零输出的条件。根据定义,输入失调电压等于使输出为零而在输入端所加的补偿电压。因此,在仅仅考虑输入失调电压时,实际运算放大器可用图2-6来等效。其中虚线右边是理想运算放大器。Vos的极性是随机的,图中的极性是任意假定的。
由图2-6可知,当n与p接地时,开环放大器的输出电压为
Vo=AoVos (2-33)
当接成闭环形式时,图2-6所示的电路变成图2-7所示。注意失调电压可以等效到放大器的同相输入端,也可以等效到反相输入端(见图2-7),但是不能等效到图2-7中B点的左边支路上。
设放大器的开环增益与输入阻抗都是无穷大。则
Vn=Vp=0

或者

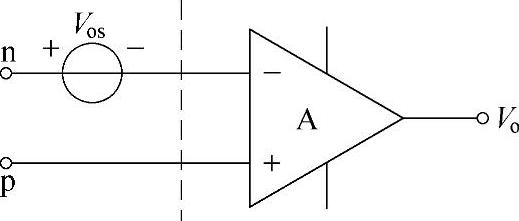
图2-6 输入失调电压的等效电路

图2-7 闭环放大器的失调
式(2-35)的推导过程并未涉及输入方式问题,所以它对同相输入及反相输入都适用。实际上如果将Vos等效到图2-7中放大器的同相端,利用同相输入放大器的增益公式(2-19)可以直接得到这个结果。
3.输入失调电流的影响
设运算放大器二输入端的偏置电流分别为IB1和IB2,接成闭环之后的电路如图2-8所示。在分析输入失调电流的影响时,假设放大器的其他参数都是理想的。
根据叠加原理,图2-8中的输出电压应由两部分叠加而成:一部分是由IB1引起的,另一部分是由IB2引起的,而且在分析其中的任一个电流时,都可把另一个视为零。
首先分析IB2的影响。IB2流过Rp后在同相输入端p产生一个电压Vp:
Vp=-IB2Rp
由理想运算放大器的同相输入增益公式(2-19)知,由IB2引起的输出电压为
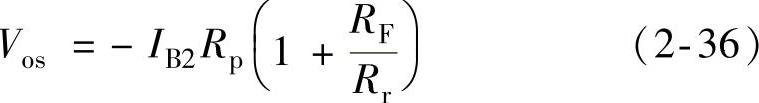
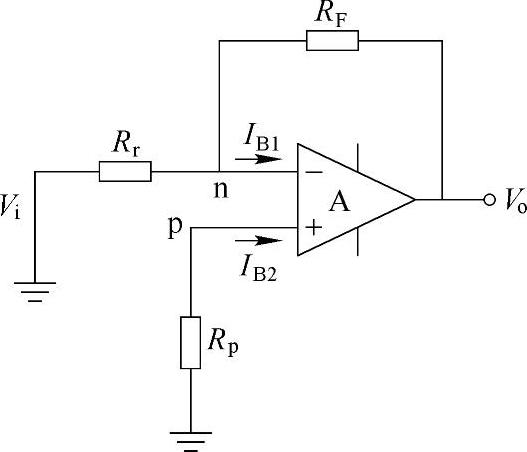
图2-8 闭环放大器的输入偏置电流
再分析IB1的影响。在分析IB1的影响时,令IB2=0,即Vp=0。假设放大器的开环电压增益为无穷大,即保证Vn=Vp=0,则Rr上的电流为零,IB1全部流过RF。所以,由IB1产生的输出电压为
Vo1=IB1RF (2-37)
总的输出电压为
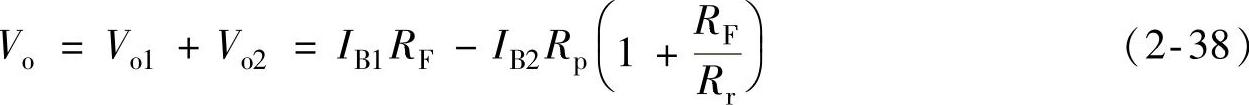
适当选取Rp,可以使式(2-38)右边两项数值相等,则由IB1和IB2引起的输出失调可以互相抵消。不过这在实际电路中很难做到,一般取
Rp=Rr∥RF (2-39)
则
Vo=(IB1-IB2)RF=IosRF (2-40)
一般Ios要比IB小一个数量级,因此按照式(2-39)选择Rp是合适的。这样,由输入失调电压和输入失调电流引起的输出失调为

Vos、Ios可正可负,计算误差时总是考虑它们可能引起的最大误差,因此,在用式(2-41)进行计算时,应该取Vos、Ios符号相同的情况估算输出失调。
输出失调其实就是输出误差,为了排除增益的因素而直接与输入信号进行比较,可把输出失调除以闭环增益,得出由Vos和Ios引入的等效输入误差。将式(2-41)分别除以反相输入及同相输入的闭环增益,得到输入失调误差为
反相输入:

同相输入:
Vo=Vos+RpIos (2-43)
其中
Rp=Rr∥RF
反相输入放大器与同相输入放大器的等效电路如图2-9和图2-10所示。
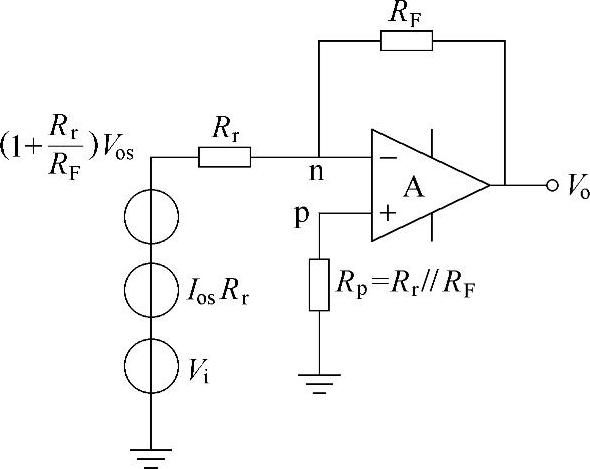
图2-9 反相输入放大器的等效电路
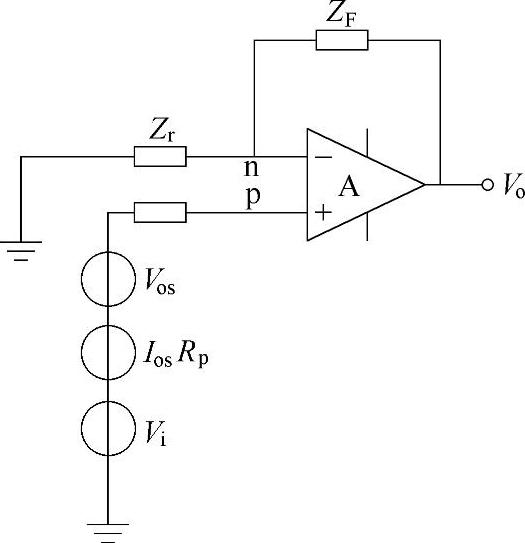
图2-10 同相输入放大器的等效电路
其中,Rr和Rp既包括外接电阻也包括信号源内阻。当信号源内阻很大时,由输入失调电流引进的误差是主要的;反之,由输入失调电压引进的误差是主要的。
输入失调电压及输入失调电流均随温度、时间和电源电压的变化而变化。所以,由它们引进的误差也随这些因素而变化,这种变化叫做温漂,也称为温度漂移。若仅考虑温度漂移,则在温度变化ΔT时,输出漂移量为
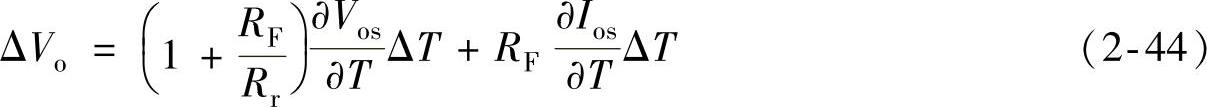
由式(2-42)和式(2-43)可求得反相输入放大器和同相输入放大器的输入端温漂量:反相输入:
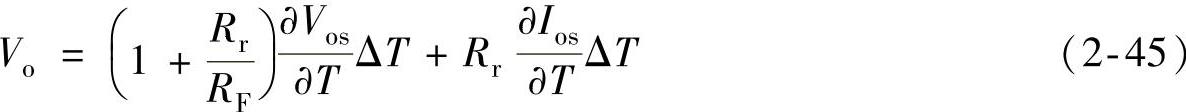
同相输入:

由式(2-2)和式(2-4)知
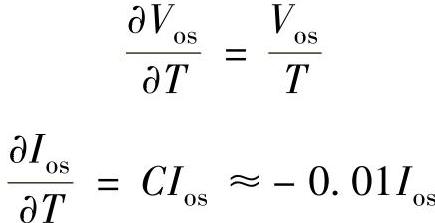 (www.zuozong.com)
(www.zuozong.com)
由此可见,放大器的温漂不仅与运算放大器的Vos和Ios有关,还与外接电阻有关。此外,反相输入与同相输入组态的输出温漂是相同的,但是折算到输入端之后却不相同,前面的式子说明了这一点。注意:图2-9中将误差等效到了放大器电路求和点的外边,才会有式(2-45)这样的结果;如果等效到求和点内,则等效到输入端的误差大小和式(2-46)是相同的,同学们可以自己推导一下。
4.由共模抑制比引进的误差
在许多应用中,运算放大器两个输入端的信号是同向的,即都是正的或都是负的。此时将两个信号的平均值定义为共模信号,以Vc表示。两个信号的差叫做差模信号,以Vd表示。即

放大器的输出电压为
Vo=AdefVd+AcomVc (2-49)
式中,Acom是放大器的共模增益;Adef是差模增益,也就是开环增益Ao。
理想运算放大器的共模增益为零,所以,输出电压中只有差模电压成分。实际放大器的共模增益不是零,所以输出电压中除了差模电压之外,还有一定的共模电压成分存在。
将式(2-9)代入式(2-49),得到:
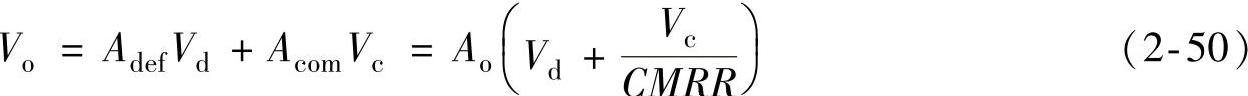
括号中为(等效)的差模输入,其中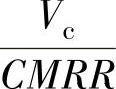 可看做由于共模抑制比有限而引入的误差项。所以,共模抑制比也等于共模电压Vc与由它引进的等效输入误差
可看做由于共模抑制比有限而引入的误差项。所以,共模抑制比也等于共模电压Vc与由它引进的等效输入误差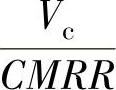 之比。
之比。
由式(2-50)可得到实际运算放大器的共模误差模型,如图2-11所示。
下面以图2-12所示的电压跟随器为例进行说明。由图可知,放大器的共模输入电压为

而输出电压为

解得

由此可见,在作电压跟随器时,开环增益与共模抑制比是同等重要的。
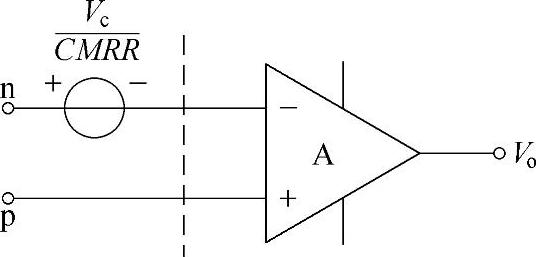
图2-11 共模误差模型

图2-12 电压跟随器
下面讨论闭环差动放大器的共模抑制能力。差动放大器的典型电路如图2-13所示,Vc是外加的共模电压。
图2-13的输出电压由两部分叠加而成:一部分是Vc加到同相端和反相端之后,由于同相输入和反相输入的增益不同而形成的,以Vo1表示:
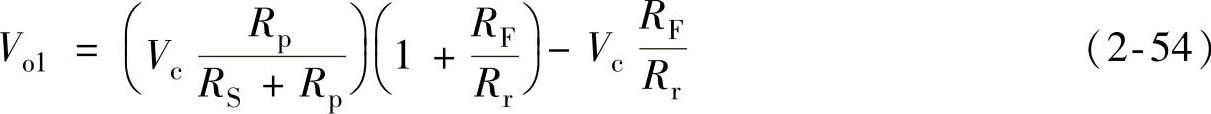
第二部分可用图2-11所示的模型把共模信号Vc等效成差模误差信号来处理,如图2-12所示。但应注意,图2-14中的Vc′是图2-13中n、p两点的共模电压,而不是外加共模信号电压Vc。由图2-13知:

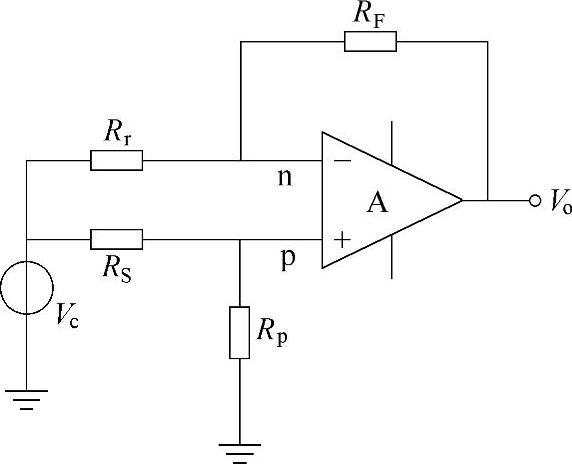
图2-13 差动放大器
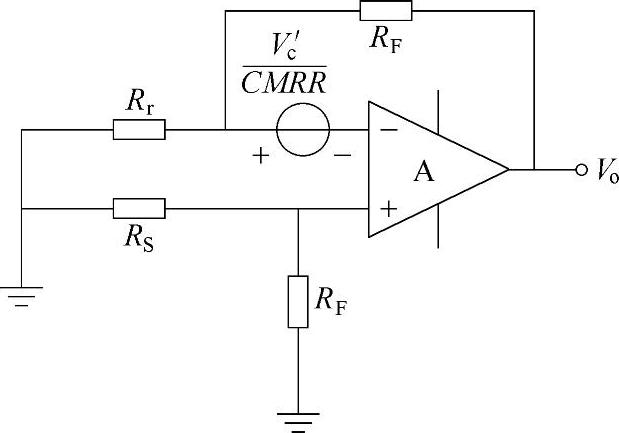
图2-14 共模电压等效电路
假设放大器的开环增益与输入阻抗均为无穷大,则仿照式(2-35)的推导方法,可以得出
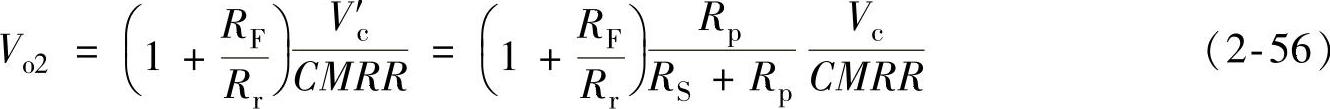
总的输出等于Vo1与Vo2之和。
若严格选配电阻,使

则

即差动放大器输出信号中共模成分的大小不仅与所用运算放大器的共模抑制比有关,还与电阻匹配及闭环增益有关。
5.频率的影响
在直流和低频下,运算放大器的开环增益是常数。随着频率的升高,开环增益下降。在零分贝以上,运算放大器的幅频特性往往有一个、两个甚至3个极点。为了使运算放大器在闭环运用时不易产生自激振荡,常用相位补偿的方法使之在零分贝以上只有一个极点,如图2-15中的曲线①所示。其中fC是极点频率,也就是开环-3dB带宽。
单极点放大器的频率特性由下式表示:

Ao是直流下的开环增益。
为了求得闭环时的幅频特性,先画出闭环放大器的框图,如图2-16所示。由图可得
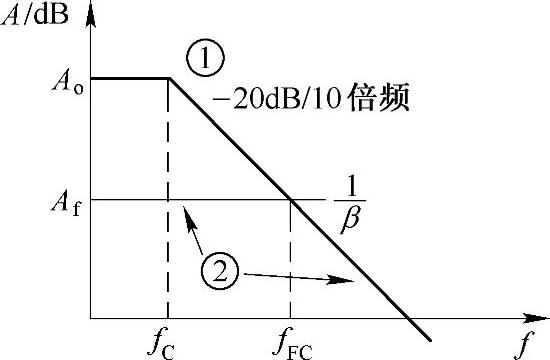
图2-15 单极点放大器的近似幅频曲线
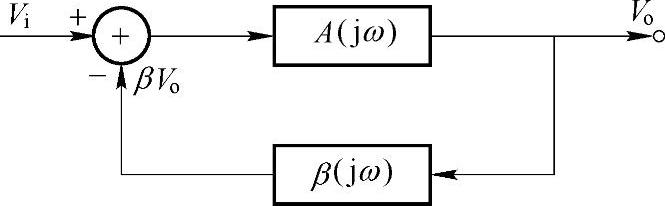
图2-16 闭环放大器的框图

因此,闭环增益为
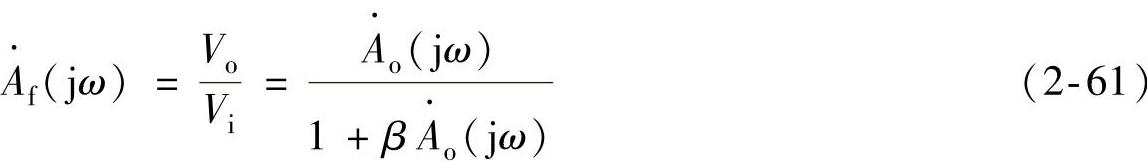
将式(2-60)代入式(2-61),得到
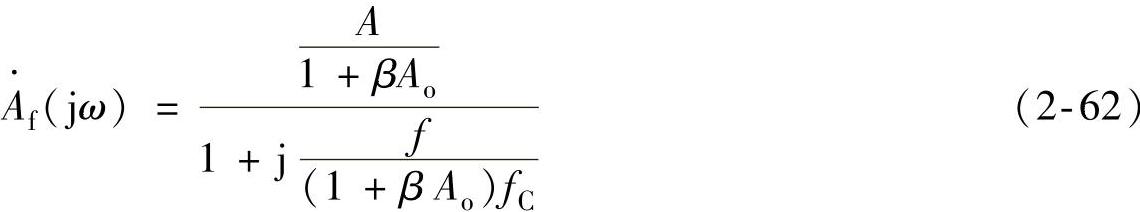
若令

则式(2-62)与式(2-59)具有完全相同的形式,即

Af是直流和低频下的闭环增益,而fFC是闭环频率特性的极点频率,或闭环-3dB带宽。
对于纯电阻性反馈网络,反馈系数β与频率无关,闭环增益的幅频曲线如图2-15中的曲线②所示。闭环增益越小,其-3dB带宽越大。
例如,μA741的开环增益典型值为20万倍,开环-3dB带宽为5Hz。当接成100倍的闭环放大器时,带宽变为10kHz;而闭环增益为10倍时,带宽为100kHz。
理想运算放大器的开环带宽无穷大,其闭环增益也不因频率而改变。当反馈系数β相同时,理想放大器的闭环增益值与实际放大器在直流下的闭环增益相同。因此,实际放大器闭环增益的频率特性公式(2-65)也可写成:

其幅频特性为

由此可见,如果信号的频率太高,实际的闭环增益将低于理想值,产生一定的误差。
一般来讲,实际使用的频率f都要低于闭环-3dB带宽。将式(2-67)展开并略去高次项,得到:

令相对误差为δ,则
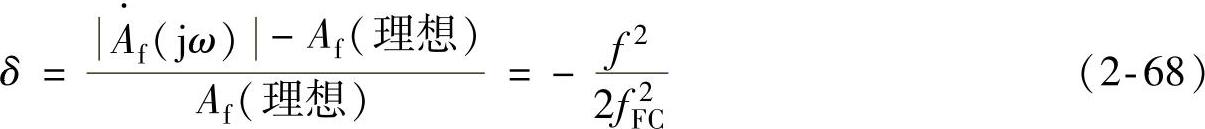
若取
f=0.1fFC
则
δ=-0.5%
6.输入阻抗的影响
输入阻抗是运算放大器的重要参数之一,尤其是在积分器、电荷放大器、峰值检波器等应用中,输入阻抗的影响更为重要。
考虑输入阻抗之后,闭环放大器的电路如图2-17a所示,Zi是放大器的输入阻抗。
为了分析输入阻抗对闭环增益的影响,利用密勒效应把电阻ZF等效成n点与地之间的、数值等于 的阻抗。假设Zi>>Rp,则图2-17a可等效为图2-17b所示的电路,其中的三角形代表输入阻抗无穷大、增益为Ao的放大器。由图可得:
的阻抗。假设Zi>>Rp,则图2-17a可等效为图2-17b所示的电路,其中的三角形代表输入阻抗无穷大、增益为Ao的放大器。由图可得:
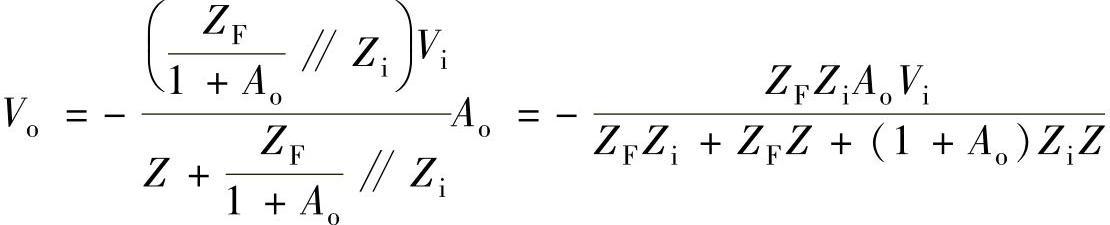
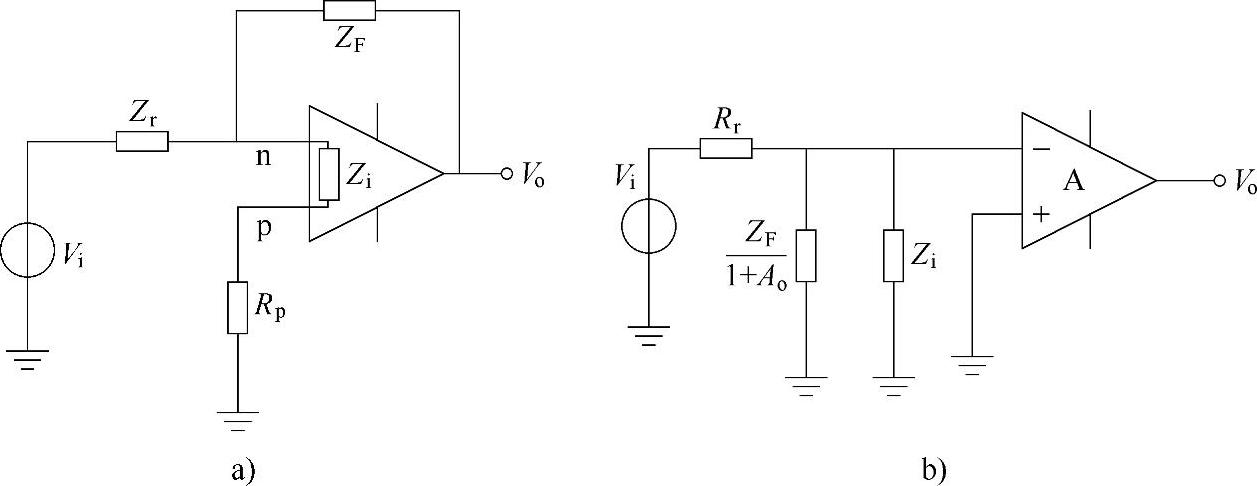
图2-17 输入阻抗模型
经过整理可以得到闭环增益
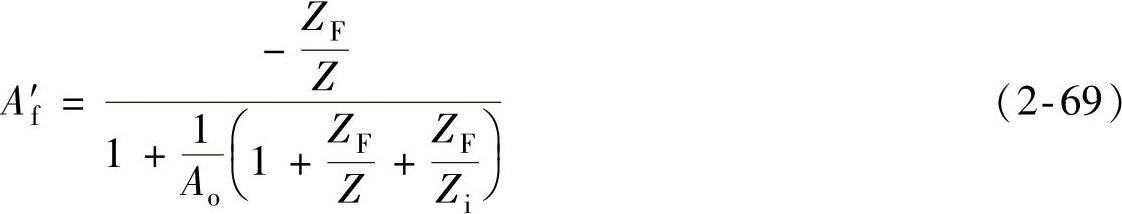
由式(2-69)可知,输入阻抗对闭环增益的影响很小,尤其是当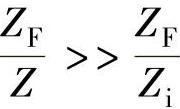 或Zi>>Z时(这在一般应用中均可得到满足)更是如此。但在高频下,放大器的输入电容会使输入阻抗变得很小,此时就应考虑它对增益的影响。
或Zi>>Z时(这在一般应用中均可得到满足)更是如此。但在高频下,放大器的输入电容会使输入阻抗变得很小,此时就应考虑它对增益的影响。
7.输出阻抗的影响
放大器输出阻抗的大小决定了它的负载性能。实际放大器的输出阻抗不可能是零,接成闭环形式之后,其输出阻抗变为

因为在应用中总有βAo>>1,而放大器的开环输出阻抗Zo一般在几百到几千欧姆之间,所以闭环输出阻抗Zout总要远远小于放大器的负载电阻,因此输出阻抗对增益的影响完全可以忽略不计。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




