微波网络的归一化波参量与散射参量分析

前面讨论的三种参量（Z、Y、A）是表示网络端口上电压与电流之间的各种关系的参量，统称为电路参量。对于这些参量，虽然从理论上给出了定义和表示式，但在微波范围内，除了TEM 模外，对于其他模，电压、电流已没有确切的物理意义，更是难以测量，因此，与此相应的电路参量也是无法测量的。但是，对于微波网络，如果利用电磁波在网络端口的参考面处的入射（入射波）和反射（反射波）现象来研究网络的特性是比较方便的，这是因为，测量电磁波的幅度和相位是比较容易做到的。具体地讲，就是利用反射系数和传输系数来研究网络各端口信号量之间的关系，我们把反映这些关系的量称为波参量：散射参量（S 参量）和传输参量（T 参量）。知道了S 和T，再利用它们与电路参量相互之间的转换公式，即可求出电路参量。在这里，只讨论表示归一化的入射波和反射波之间关系的网络参量，称为归一化的波参量（简称波参量）。

（一）微波网络的散射参量

在空间传播的电磁波，当遇到障碍物时，会从其上向四面八方传播，这种现象称为散射。在微波系统内部传输的电磁波遇到结构上的不均匀性时，也会产生散射，但散射波不可能四面八方地传播，它只能通过波导或微波元件的端口散射出去，而入射波也只能通过端口进入微波系统，因此，把描述这种现象的参量称为散射参量。对于散射参量可以利用电桥、定向耦合器、反射计等来测量，也可以利用矢量网络分析仪来测量。

1.二端口网络的散射参量

如图7.4-5所示的二端口网络，其端口信号量分别为（a1，b1）和（a2，b2）；a1和 a2为场强复振幅的归一化值，称为归一化入射波（规定进入网络的波为入射波），1b 和也为场强复振幅的归一化值，称为归一化反射波（规定离开网络的波为反射波）。根据电磁场理论，得

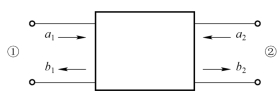
图7.4-5 二端口网络的波参量

或写为

简记为

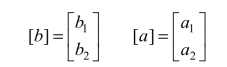
式中它们分别为由端口的反射波和入射波构成的列矩阵（列矢量），而则称为二端口网络的归一化散射矩阵，其元素 S11、S12、S21和 S22称为归一化的散射参量。

网络的散射参量是在各端口接匹配负载的情况下来定义的，它具有明确的物理意义。“当端口②接匹配负载时，a2=0，式（7.4-33）变为

则

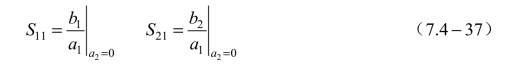
当端口①接匹配负载时，a1=0，式（7.4-33）变为

(www.zuozong.com)

则

式（7.4-37）和式（7.4-38）为散射参量的定义式。S11和 S21分别表示端口②接匹配负载时，端口①波的反射系数和端口①到端口②波的传输系数；S22和 S12分别表示端口①接匹配负载时，端口②波的反射系数和端口②到端口①波的传输系数。

2.n 端口网络的归一化散射参量

具有n 个端口的网络的归一化散射参量，可由二端口网络的归一化散射参量推广而得，即

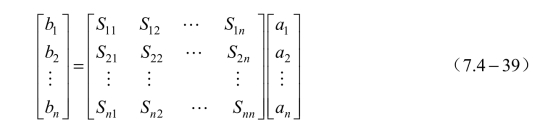
式中

简记为

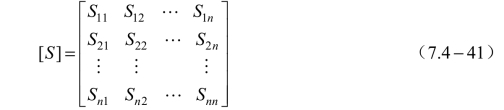
称为n 端口网络的散射矩阵，它是一个方阵，共有2

n 个元素，称为n 端口网络的散射参量，其定义式为Sii表示除端口i 外，其他端口均接匹配负载时，端口i 波的反射系数；Sji表示除端口i 外，其他端口均接匹配负载时，端口i 到端口j 的波的传输系数。

（二）二端口微波网络的传输参量

二端口网络的传输参量对于图7.4-5所示的二端口网络，根据电磁场理论可得

或写为

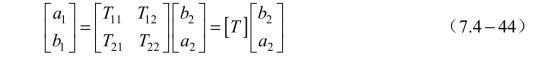
式中

称为二端口网络的传输矩阵，其元素称为传输参量。二端口网络的传输参量，除了 T11表示端口②接匹配负载时，端口①到端口②的波的传输系数的倒数外，其他参量并无明确的物理意义。