谐振腔的等效电路简介

在§5.1 中曾提到过谐振腔等效电路的问题，并做了简要的说明。本节对此问题再做进一步的补充和分析。

利用等效电路的概念不仅能比较形象地描述腔的谐振特性，而且在实际的工程计算中也具有一定的实用价值。一个实际的谐振腔，它或者作为接收信号源能量的负载，或者作为向其负载输送能量的振荡源。总之，它要与外部电路（例如微波元、器件等）发生耦合。因此，谐振腔对于外部电路所呈现出的谐振特性和其他的外部特性，往往是我们关注的主要问题，而对于腔内的场结构并不提出什么特殊的要求。针对这种情况（以及其他的类似情况），利用谐振腔等效电路的概念，不仅避免了用场的方法解决问题时所带来的困难、简化了计算，而且也满足了一般工程计算的要求。关于等效的方法，扼要地说，就是：首先利用计算或测量的方法求出谐振腔的特性参数，然后根据腔的特性参数与集总参数谐振回路特性参数之间的等效关系式求出等效电路的等效参数。下面就来讨论这一问题。在§5.1 中曾提到，对于工作于某一模式的谐振腔，在一狭窄的频率范围内，可将其等效为集总参数的并联或串联谐振回路（这取决于参考面位置的选择）。本节只着重讨论把腔等效为并联谐振回路的问题，对于把腔等效为串联谐振回路的问题，则只给出必要的结论，而不予详细讨论。

首先讨论图5.5-1所示集总参数并联谐振回路本身的问题，然后再讨论在什么条件下可以把谐振腔等效为集总参数的并联谐振回路，以及如何求出等效回路的等效参数问题。图中的L、C 和G 分别为并联谐振回路的电感、电容和电导，Um为回路电压的幅值。由此可得并联谐振回路的储能W、损耗功率P 和固有品质因数Q 的表示式分别为

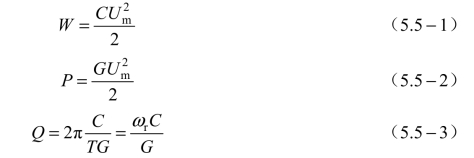
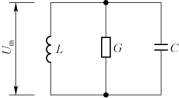
图5.5-1 微波谐振腔的等效电路

式中的是回路的谐振角频率，T 是谐振周期。为了把谐振腔等效为集总参数的并联谐振回路，求出其等效条件和等效参数，还需要对图5.5-1所示的并联回路做进一步的分析。设Y 为回路的导纳，则

式中的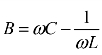是回路的并联电纳。因为，所以可将B 写为

如果工作角频率ω 与ωr相差很少，则可近似地认为ω +ωr≈2ω，这样，就可将B 近似地写为

将该式对ω 求导，即得到B=f（ω）在ωr附近随ω 的变化率为

由此式可知，可以将电容C 表示为

即并联谐振回路的电容C 可用ω 接近ωr时电纳B 的变化率来表示。根据式（5.5-3），并联谐振回路的Q 可表示为

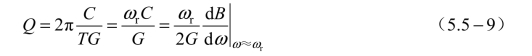
或

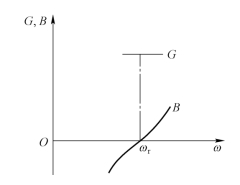
图5.5-2 谐振角频率附近并联谐振回路的电导和电纳曲线

式中的λr是并联谐振回路的谐振波长，λ 是工作波长。因为在ωr附近很窄的频带内由趋肤效应所引起的G 的变化是很小的，所以可近似地认为G 是不变的，是一个常数。

由以上的分析可以看出，集总参数的并联谐振回路在其谐振角频率附近很窄的频带内具有三个特性：电纳曲线B=f（ω）与 ω 呈线性关系，而且 dB/dω ＞0；电纳曲线B=f（ω）当ω=ωr时通过零点；电导G 近似等于常数。这些特点也可以用图来加以说明，如图5.5-2所示。(www.zuozong.com)

对于集总参数的并联谐振回路，实际上并不需要根据式（5.5-8）、式（5.5-9）或式（5.5-10）求出其电容C 和固有品质因数Q，因为有比这更简便的公式可以利用；导出上述的公式、分析集总参数并联回路在其谐振角频率附近很窄频带内所具有的特性等，目的不是解决集总参数回路本身的问题，正如前面已指出过的，而是需要知道谐振腔满足什么条件，才可以将它等效为集总参数的并联谐振回路，并进而求出其等效参数。

综合以上的分析可以得出这样的结论：对于一个工作于某一模式的谐振腔，在很窄的频率范围内，如果也具有上述的集总参数并联谐振回路的三个特性，那么，就可以将它等效为一个集总参数的并联谐振回路，并可根据有关的关系式求出其等效参数。理论和实验均已证明，谐振腔也具有这三个特性，因此可以将它等效为一个集总参数的并联谐振回路。如果我们假定图5.5-1 就是谐振腔的集总参数的等效并联谐振回路，那么，两者的等效关系为：等效回路的电导G 应与谐振腔在谐振时的等效电导G0相等；等效回路的电纳在谐振角频率附近的变化率应与谐振腔的电纳在谐振角频率附近的变化率相等。根据这些等效原则就可求出等效并联谐振回路的具体参数。设L、C 和G 分别为等效回路的电感、电容和电导，Um为回路电压的幅值，并假设谐振腔的谐振角频率为ωr、损耗功率为P、固有品质因数为Q0，电导为G0，那么，在谐振状态下，等效回路的参数与谐振腔的参数之间的关系为

对于谐振腔如果能够用理论计算或实际测量的方法求出腔的ωr、P、Q0和G0等参数，那么，等效并联谐振回路的参数也就确定了，即

现以λr/4 型同轴线谐振腔（模式为TEM）为例来说明谐振腔等效为集总参数并联谐振回路的问题。根据式（1.3-44）可知，对于一端短路、另一端开路、长为l（指腔内长度）的λr/4 型无耗同轴线谐振腔，从其开路端向短路端看去的输入阻抗为

输入导纳为

电纳为

或

式中的v 是在与腔中填充的相同的无界介质中电磁波的速度。电纳B=f（ω）的曲线如图5.5-3所示。从图5.5-3 即可看出，λr/4 型同轴线谐振腔在其谐振角频率附近很窄的频带内，与前述的集总参数并联谐振回路在其谐振角频率附近很窄的频带内所具有的特性是一样的，因此可将同轴线谐振腔等效为集总参数的并联谐振回路，并可根据有关公式求出其等效参数。

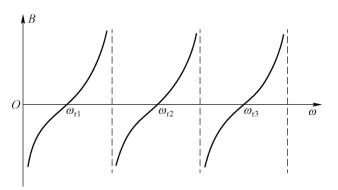
图5.5-3 λr/4 型同轴线谐振腔的电纳曲线

如果将谐振腔等效为集总参数的串联谐振回路，那么，经过与上述的类似分析过程，即可得到集总参数串联谐振回路的下列关系式

或

式中的L、R、X 和Q 分别为串联谐振回路的电感、电阻、电抗和固有品质因数。回路在其谐振频率附近很窄的范围内具有这样的特性：电抗曲线X=f（ω）与ω 呈线性关系；而且，dX/dω＞0；电抗曲线X=f（ω）当ω=ωr时通过零点；电阻R 近似等于常数。理论和实验可以证明，谐振腔也具有这些特性，因此可将其等效为集总参数的串联谐振回路，并可求出相应的等效参数。

以上的分析是仅就孤立的谐振腔与集总参数谐振回路之间的等效关系而言的，而实际的腔体总是要通过耦合机构与外电路发生联系的，耦合机构和外电路都会对腔的参数产生一定的影响。对于这些问题，读者可参阅有关的资料，这里就不讨论了。