阶跃光纤的射线分析

如同在前面所讲的光线在不同介质的分界面处产生全反射，从而形成沿z 方向传播的波一样，当光线投射到光纤芯子的端面，并进入到光纤中时，就会在芯子与包层的分界面处产生全反射，形成沿光纤轴线传播的波。现在要讨论的问题是，投射到芯子端面上的光线应满足什么条件，才能在光纤中产生全反射，并形成沿轴线传播的波。对此，可以利用射线理论来分析。在这里需要说明的是：虽然芯子与包层的分界面不是平面，而是曲面，但是，当芯子表面的曲率半径比工作波长大得多时，仍可以近似地把它看作是平面。根据前面的讨论可以推知，在全反射的情况下，光线渗透到包层内的距离是很短的，因此只要包层的厚度远大于渗透距离，就可以近似地认为它是无限厚的，这样，就可以不考虑第二个分界面（包层与保护层或空气的分界面）的影响，从而使问题得到简化。由于多模光纤芯子横截面的尺寸比工作波长大得多，因此对于投射到芯子端面上的光线而言，可以把端面看作是无限大的平面，这样，就可以用射线理论来分析光纤的传输特性，并能得到较好的结果。由于单模光纤芯子横截面的尺寸比工作波长大不了多少，因此对于光线而言，芯子的端面就不能被看作是无限大的平面，也就是说，射线理论不适用于单模光纤。

根据光线在光纤芯子里的不同传播方式，可以把它们分为子午射线、斜射线和螺旋线三种类型。在此，只讨论前两种类型光线的传播情况。下面分别讨论。

（一）子午射线分析

首先讨论子午射线在芯子与包层分界面处产生全反射时，它应满足的条件，然后讨论子午射线的色散问题。

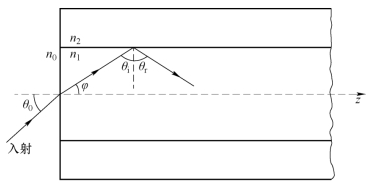
图4.2-3 子午射线

1.全反射的条件

图4.2-3 是子午射线的传播情况。芯子（其半径为a）和包层（设其厚度为无限大）的折射率分别为n1和n2（n1＞n2），设光纤端面（z=0 处）左方介质的折射率为n0（真空或空气的折射率），光线从与z 轴成θ0夹角的方向投射于端面。包含光纤轴的平面称为子午面，若光线在传播过程中，其路径始终在子午面内，则称为子午射线。可见，这是与光纤轴线相交的一种射线。现在来讨论θ0应满足什么条件，才能使光线进入光纤之后在芯子与包层的分界面处产生全反射，从而形成沿光纤轴线方向传播的波。

根据斯涅尔定律，当光线从端面进入光纤之后，应有

即

式中的φ=90°-θi。在芯子与包层分界面处产生全反射的条件为θi≥θc，即

由此可知

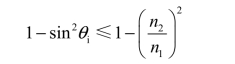
又因为

将其代入式（4.2-20）中，得

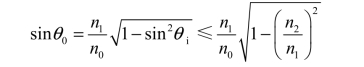
即

这就是在全反射的情况下，θ0或子午射线应满足的条件。其中，允许的最大的θ0应满足

即是说，若以θ0max为顶角构成一个圆锥体，那么，凡是在此圆锥体内的光线投射到芯子的端面，并进入光纤之后均可以在分界面处产生全反射，从而形成沿光纤轴线方向传播的波，因此，通常把θ0max称为最大激励（接收）角。在光学的透镜系统中，当光轴上的物点相对于入射孔的张角为α 时，一般称α 的正弦sinα 为数值孔径，并用符号NA（Numerical Aperture）来表示之。它表示，只有其传播方向与光轴的夹角小于α 的那一部分光线才能被透镜所接收，即数值孔径表示透镜的聚光能力。类似地，在光纤中也可以用数值孔径来表示光纤的聚光能力，它的表示式为

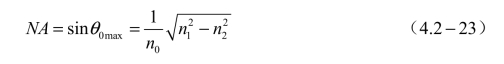
对于空气介质，n0≈1，则

数值孔径越大（n1与n2的差别越大），光纤接收光线的能力越大，光纤也越易被激励。但是，其值也不宜太大，否则会使光纤的色散增大、带宽减小，因此NA 的范围为0.15～0.24。

对于渐变型光纤也可以求得数值孔径的表示式，但是正如式（4.1-1）所表明的那样，由于芯子的折射率n1（r）是随着芯子的半径r 而变化的，因此不可能写出一个总的数值孔径的表示式，而只能写出局部的（芯子横截面上各点处的）数值孔径的表示式，即

式中的n2是包层的折射率。当r=0 时（芯子中心线处），NA（r）有最大值，即

式中的n1（0）是芯子中心线处的折射率。

2.子午射线的色散

所谓色散，就是光波（光能量）沿光纤轴向的相移常数或传播速度不同。色散会引起传输信息的失真。光纤中产生色散的原因有三种：一是模式之间的色散（模式或模间色散），即在同一频率下，当有多个模式在光纤中传输时，由于各个模式的传播速度不同而引起的色散；二是波导色散，它是模式本身的色散（模内色散），即在同一模式下，不同的频率传播速度不同而引起的色散；三是材料色散，即光纤所用材料的折射率不是常数，而是随着频率而变化的，因此，传输信息中各个频率成分的传播速度也不相同，形成了色散。需要指出的是，在实际中光纤所产生的色散，不一定是由一种原因造成的，而可能是由多种原因造成的，例如在单模光纤中，既有波导色散，又有材料色散。

子午射线的色散属于模式（间）色散。如图4.2-3所示，从射线理论的观点看，当频率相同但入射角（θi≥θc）不同的光线投射到芯子与包层的分界面处，并产生全反射时，它们沿光纤轴向的速度是不同的，或者说，光线从光纤始端到终端传播的路径不同，到达终端的时间也不同，产生了时延差，从而造成了传输信息的失真。这种现象称为子午射线的色散。从另一方面看，投向芯子与包层分界面处的入射波与由分界面处返回的反射波相叠加，在芯子的横截面上形成了纯驻波场，入射波的入射角（θi≥θc）不同，则入、反射波相叠加后形成的场结构（场分布）也不同，即模式不同，传播速度不同，产生了色散。可见，子午射线的色散属于模式（间）色散。(www.zuozong.com)

现在我们来计算子午射线所产生的最大时延差，由此可以对子午射线的色散有进一步的了解。如图4.2-3所示，设光纤的长度为l，从光纤始端（z=0 处）到终端传播得最快的是与光纤轴线相平行的射线（θi=90°），令其速度为vmax，则射线从始端到达终端所需要的时间为

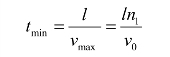
式中，n1是芯子的折射率；v0是光线在真空中的速度。从光纤始端到终端传播得最慢的是入射角θi=θc的射线，设该射线投向芯子与包层分界面处的速度为v（即射线在与芯子相同的无界介质中的光速），那么，它沿光纤轴向的速度则为

式中，θc为产生全反射时的临界角；n2是包层的折射率。射线从始端到达终端所需要的时间为

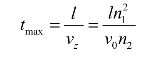
两种射线的最大时延差为

若n2与n1相差很少（即弱导光纤），则最大时延差τ可近似地写为

式中的Δ为相对折射率差。可见，Δ越小，τ也越小，即色散也越小。例如，设Δ=1%，n1=1.50，则每千米的最大时延差τ=50 ns。另外，从阶跃光纤的波动理论可知，当频率一定时，Δ越小，光纤中所能传输的模式的数量也越少，这样，就减少了模间色散。

（二）斜射线分析

图4.2-4 是斜射线的传播情况，光纤芯子（其半径为a）和包层（设其厚度为无限大）的折射率分别为n1和n2（n1＞n2）。所谓斜射线，即光线在芯子里的传播路径不在同一个平面内，也不与光纤轴线相交，而是一个螺旋形的空间折线。如图4.2-4所示，假设有一光射线沿着S 的方向投射到光纤端面上的某一点P0，进入芯子内，现在讨论：投射到P0点的光射线应满足什么条件，才能使它进入芯子之后在芯子与包层的分界面处产生全反射，从而形成沿光纤轴线方向传播的波。为便于分析，采用如图4.2-4 中所示的直角坐标系，设x、y 和z 分别为沿相应坐标轴正方向的单位矢量。这样，在光纤端面上入射线方向的单位矢量即可写为

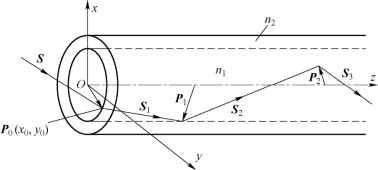
图4.2-4 斜射线

式中的L0、M0和N0为入射线的方向余弦。光射线的入射点P0（x0，y0）可以用该点的矢径P0来表示，即

光射线进入芯子之后，在芯子与包层的分界面处产生反射。可以设想，在每一反射点处作通过该点的切平面的垂线（切平面与分界面相切，其切线与光纤轴平行），垂线与光纤轴线相交，从而构成了每一反射点处切平面的法向矢量；设在第m（m=1，2，3，…）个反射点处入射线方向的单位矢量为Sm，入射角为θim，反射线方向的单位矢量为Sm+1，反射角为θrm，该点的单位法矢量为Pm。这样，光学中“入射线、反射线和法线应在同一个平面内”的规律，就可以用数学式子表示为

光学中“入射角和反射角相等”的规律，则可表示为

光射线在芯子与包层分界面处产生全反射的条件，根据式（4.2-9）应为

为书写方便，将θim写为θi，θc为产生全反射时的临界角。由此式可得

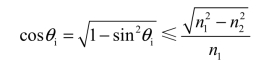
现将其改写为

将此式应用于光纤始端的端面上，则有

或写为

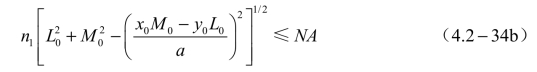
式中的NA 为子午射线时的数值孔径。这就是说，如果光纤始端的光射线满足上式，则进入光纤芯子内的光射线就会在芯子与包层的分界面处产生全反射，从而形成沿光纤轴线方向传播的波。作为一种特殊情况，即光射线在端面上的入射点P0位于x 轴上时（|x0|=a，y0=0），则式（4.2-34b）变为

该式与M0无关，即入射光线与y 轴的夹角可任意选取。由于光纤对其轴线是旋转对称的，x和y 坐标轴可任意选取，端面上任意一点的径向矢量均可看作位于x 轴上。因此，对于任意入射线，若它与包含有入射点的径向矢量之间夹角的余弦满足式（4.2-35），则均能进入光纤内，形成全反射，并沿光纤轴向传播。对于几乎与y 轴相垂直的入射线，虽然也会被限制于芯子内产生全反射，但它沿光纤轴向的速度近乎为零，而不能传播。斜射线的最大激励角比子午射线的最大激励角要大，即是说，斜射线更易被光纤所收集。

光线在光纤芯子里的传播路径除上述的子午射线和斜射线外，还有一种是螺旋线，即光线沿着芯子与包层的分界面、边绕光纤轴旋转边沿轴向传播，形成一个空间螺旋线。对于这种情况，这里就不讨论了。