用保角变换法求带状线的特性阻抗详解

本附录的内容是：首先简单地说明一下求带状线的特性阻抗时所用的保角变换式，然后讨论用保角变换的方法求带状线和耦合带状线的特性阻抗的问题。

（一）许瓦兹-克力斯托夫变换式

当均匀无耗带状线传输的是主模TEM 时，如图3.1-1所示，它的特性阻抗Zc为

L 和C 分别为带状线单位长度上的分布电感和分布电容。我们知道，电磁波在线中的相速vp等于，或者。若再假定μ≈μ0，v0是电磁波在真空中的速度，则，而带状线的特性阻抗Zc即可写为

可见，只要求出了电容C，则Zc就可以很容易地求出来。但是，由于带状线横截面形状复杂，电容是不均匀的，因此不便于直接求出C 的值。为了求出C，需要将带状线较复杂的横截面的边界条件，利用复变函数中保角变换的方法将其变换（映射，映照）为横截面形状比较简单、便于求出电容C 的边界，从而求出带状线的特性阻抗Zc。在保角变换中用得较多的变换式就是许瓦兹-克力斯托夫（Schwarz-Christoffel）变换式，关于这个变换式的推导和证明，读者可参阅有关的数学书，在此不予详述。但是，为了对该变换式有个初步的理解，并会应用它，对它做一些简略的说明还是必要的。下面就讨论一下这个问题。

在数学中我们知道，设复变数z=x +jy 在复平面某域（定义域）D 内取值，如果有一个确定的法则存在，根据这一法则，对于域内每个可能取的z，就有一个或几个相应的复数W=f（z）=u（x，y）+jv（x，y）随着而定，则称复变数W 为复变数z 的函数（简称复变函数）。若函数f（z）在其定义D 内的某一点zo，以及zo的邻域内处处可导，则称f（z）在zo解析；若f（z）在定义域D 内每一点解析，则称f（z）是域D 内的一个解析函数（或称正则函数）。解析函数的充分和必要条件是：函数f（z）=u（x，y）+jv（x，y）在其定义域D 内任一点z 及其邻域内都是可导的，并满足柯西-黎曼方程（简称C-R 方程），即

显然，解析函数f（z）的实部u 和虚部v 都满足二维拉普拉斯（Laplace）方程，即它们都是拉普拉斯方程的解，在电学中为二维静电场的解。若解析函数f（z）的导数f′（z）不为零，也不为无穷大，则f（z）具有保角变换的性质（当导数为零时，其模为零，幅角为不确定值；当导数为无穷大时，其模不为有限值，这两种情况保角变换均失去意义）。例如，在W=f（z）的复平面上，若u=常数和v=常数的两条曲线是正交的，那么，与此相对应的在z 的复平面上，u和v 都为常数的两条曲线也是正交的。由于在静电场中等电位线与电力线是正交的，因此，若取u=常数的线表示等电位线，则v=常数的线就表示电力线，反之亦然。根据电磁场理论可知，在W=f（z）复平面上等位线间的电场储能与z=x +jy 复平面上相应等位线间的电场储能是相等的，即是说，对于W 面上的两个导体而言，经变换到z 面之后，尽管两个导体的形状、位置和场分布发生了变化，但两导体之间的电容与W 面上两导体之间的电容是相等的。显然，这个结论，对于把z 面的两个导体变换为W 面上的情况，也是正确的。

需要指出的是，保角变换只适用于二维的静电场，电位分布函数必须满足拉普拉斯方程，因此，一般地讲，它不能用于时变场（不满足拉普拉斯方程）。但是，在双导线传输线传输TEM 模的情况下，其横截面内的场结构与同样边界条件下静电场的场结构是相同的，因而保角变换仍是有效的。这样，就可以利用解析函数的特性，选取适当的变换函数，将带状传输线较为复杂的横截面边界经过一次或多次的变换，使其成为易于求出电容C 的简单边界。带状传输线横截面的边界呈多角形，对此可采用不同的变换函数将其变换为形状较为简单的边界，其中许瓦兹-克力斯托夫变换式是常用的变换，下面对它做一简略的说明。

利用许瓦兹-克力斯托夫变换式，可以将一个复平面上的多角形域变换为另一个复平面的上半平面，或者将一个复平面的上半平面变换为另一个复平面上的多角形域。如附图3.1-1所示，设函数W=f（z）=u（x，y）+jv（x，y），z=x +jy。在W 复平面上多角形域顶点处的W 分别为W1、W2、W3、…、Wn、相应的内角依次为α1、α2、α3、…、αn，在z 复平面的实轴上，依据函数关系与W 复平面上的W1、W2、W3、…、Wn相对应的点分别为x1、x2、x3、…、xn，而且x1＜x2＜x3＜…＜xn。这样，利用许瓦兹-克力斯托夫变换式，即

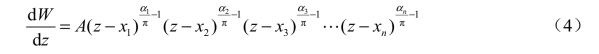
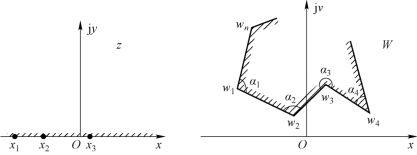
附图3.1-1 许瓦兹变换

或写为

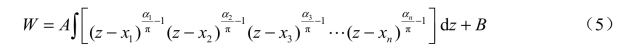
就可以将W 面上的多角形域变换为z 面的上半平面。式中的A 和B，一般是复常数，A 可以使多角形域的方位和大小发生变化，B 可以使多角形域发生位移。在x1、x2、x3、…、xn中只有三个数可以任意选定，其余的数可以通过z 面上x1、x2、x3、…、xn与W 面上的W1、W2、W3、…、Wn之间的对应关系，经计算而求得。对于实际问题中遇到的不是封闭的多角形域，变换式（4）或变换式（5）仍然成立，此时可以认为多角形域的某个顶点在无穷远处，对于多角形域处于无穷远的这个顶点，可在一系列的x 中任选一个，例如xk，使xk=∞与之相对应，这样，在数学中已经证明，变换式（4）和变换式（5）中的，从而使变换式得以简化，变为

或

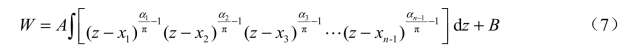
如前所述，在函数的导数f ′（z）=0 或等于无穷大的点，变换失去了保角性，因此在式（4）～式（7）中，在z=x1、x2、x3、…、xn等点，变换失去了保角性。除此而外，f ′（z）≠0，即在Im（z）≥0 的区域（上半平面）是保角的。这样，在z 面上当z 在实轴上从左向右移动，并经过x1、x2、x3、…、xn诸点时，在W 面上与之相对应的W 按逆时针的绕向沿着多角形域的边界移动，从而完成了W 面与z 面之间的变换。

为了便于应用许瓦兹-克力斯托夫变换式，我们对它可以做一简略的说明，以帮助理解。为此，首先讨论幂函数，然后再根据幂函数的变换式来讨论许瓦兹-克力斯托夫变换式。设有幂函数

并设z=rejθ，则

除了z=0 之外，式（8）是一个保角变换。该变换式将z 平面上以坐标原点为圆心、以|z|=r为半径的圆周变换为W 平面上以坐标原点为圆心、以|W|=rn 为半径的圆周，或者将z 平面上以θ 为辐角的射线变换为W 平面上以nθ 为辐角的射线，z 平面上0＜θ＜θo的角形域变换为W 平面上0＜nθ＜nθo的角形域。显然，在z 平面上0＜θ＜2π/n 的角形域变换为W 平面上0＜nθ＜2π 的区域，即除去正半实轴之外的W 平面。当把一个角形域变换为另一个角域时，经常用到的就是幂函数。

仿照式（8）的幂函数，可以作如下的函数

当z=x1时，对应着W=W1，即在z 平面实轴上的一点x1与W 平面上的一点W1相对应；若在z 平面上以x1为顶点的角形域为0～π（即z 平面的上半平面），那么，根据幂函数的性质，变换到W 平面上就是以W1为顶点、张角为的角形域，如附图3.1-2所示。由此可以推想，若在z 平面的实轴上取若干点：x1、x2、x3、…、xn，是否可以将z 平面的上半平面变换为以W1、W2、W3、…、Wn为顶点的多角形域呢？可以证明（证明从略），情况正是如此。为了与许瓦兹-克力斯托夫变换式相比较，可以对式（9）求导，即

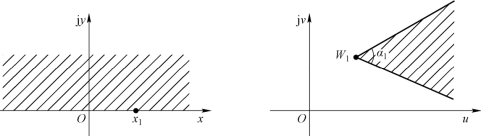
附图3.1-2 幂函数

这是指在W 平面上只有一个顶点的情况，若在W 平面上有若干个（有限的）顶点，那么，对于每个顶点而言都应有因子出现，因此，可以推想，当考虑到W 平面上多角形域所有的顶点时，就会得到如式（4）和式（5）所示的许瓦兹-克力斯托夫变换式。当然，这种推想并不能代替严格的推导，但是，却有助于对该变换式的理解和应用。

（二）对称带状线的特性阻抗

对称带状线的结构与尺寸如图3.1-1所示。上下两导体板之间的距离为b，中心导体带的厚度为t、宽度为w。现在利用保角变换的方法求出它单位长度上的电容C，以及特性阻抗Zc。为此，可以把带状线横截面所处的平面看作复平面z，如附图3.1-3（a）所示。由于结构上的对称性，因此可以取x 和y 轴分别作为带状线的上下两部分和左右两部分的对称轴。这样，只需要求出带状线右半部分的电容（图中有斜线的部分），然后再乘以2，就得到全部的电容C，再根据式（2）即可求出特性阻抗Zc。

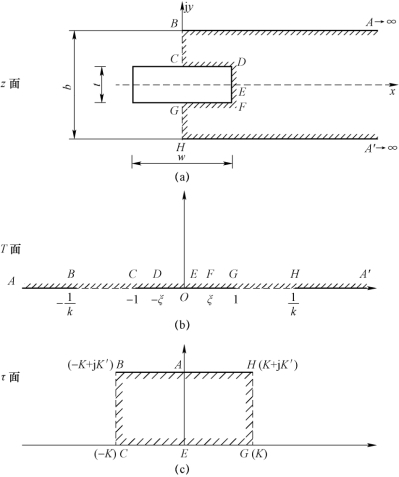
附图3.1-3 对称带状线的横截面及其变换

设带状线的内导体处于高电位，上下导体板为零电位。显然，电力线与BC 和GH 的方向是一致的，而磁力线则与之相垂直，即BC 和GH 是磁壁。首先，把附图3.1-3（a）复平面z 上由带状线横截面的右半部分所构成的多角形域ABCDEFGHA′利用许瓦兹-克力斯托夫变换式变换为附图3.1-3（b）复平面T 的上半平面，然后再将该上半面利用许瓦兹-克力斯托夫变换式变换为附图3.1-3（c）复平面τ 上的矩形域，这个矩形域的电容是均匀的，据此即可求出带状线的电容C，并进而求出特性阻抗Zc。下面详述其变换过程。为了方便，在变换过程中，各复平面上的对应点均用相同字母表示。

1.将复平面z 上的多角形域变换为复平面T 的上半平面

为了利用许瓦兹-克力斯托夫变换式，可以将上下导体板向右方无限延长（A→∞和A′→∞），并在无穷远处相交于一点，该点对应的内角为零。这样，在z 平面上ABCDEFGHA′就构成了一个封闭的多角形域。如前所述，在利用式（4）或式（5）时，可以在T 平面上任选三个点，现在选T 平面实轴上的 +1、-1 和∞这三个点；实轴上的ξ 和k 是与带状线尺寸有关的待定值（ξ 和k 均小于1）。现将z 平面与T 平面上对应点的坐标，以及z 平面上多角形域各顶点的内角αn和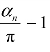等列表如下：

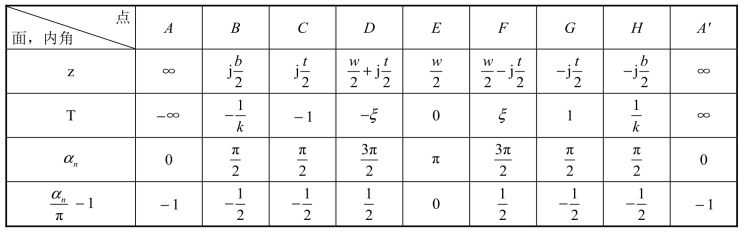
根据表和许瓦兹-克力斯托夫变换式可得

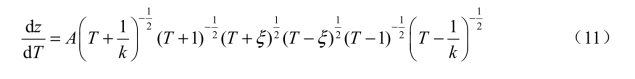
或写为

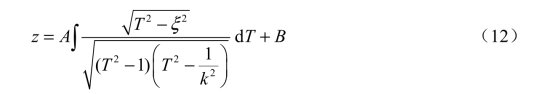
式中的B 为待定的积分常数（实数或复数），待定的参数ξ 和k 可暂时看作常数，而对T 积分，在根据带状线的尺寸确定了ξ 和k 之后，式（12）的具体表示式也就确定了。式（12）属于椭圆积分类型，不能表示为初等函数的形式。但是在给定了积分限的情况下，其积分可表示为级数的形式，或查椭圆积分表求得。在这里，当带状线的尺寸（w，b，t）已知时，可以根据z 平面与T 平面对应线段之间的关系，采用分段积分的方法求出ξ 和k 与尺寸之间的关系式。现在把分段积分的结果写在下面，并以I（T1，T2）表示椭圆积分的值。在z 平面上，从E 到F 的积分为

在T 平面上与之相对应的从E 到F 的积分为

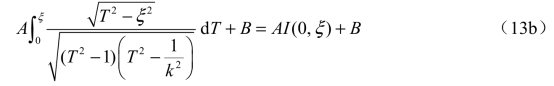
在z 平面上，从F 到G 的积分为

在T 平面上与之相对应的从F 到G 的积分为

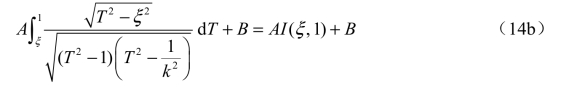
在z 平面上，从G 到H 的积分为

在T 平面上，与之相对应的从G 到H 的积分为

为了确定以上各式中的积分常数B，还需要再求出一个两复平面（z 与T）对应线段之间的积分，如在z 平面上从E 到D 的积分为(www.zuozong.com)

在T 平面上，与之相对应的从E 到D 的积分为

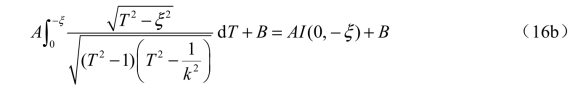
或写为

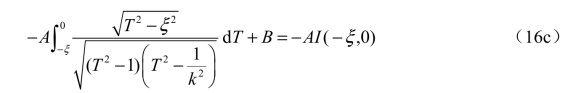
将式（13a）与式（16a）相加，与此相对应，将式（13b）与式（16c）相加，则得

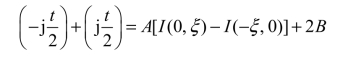
等号右端方括号内两个积分的被积函数是完全相同的偶函数，因此它们的积分之差应为零，由此可得积分常数B 为零。

由以上各式可以得到下列的关系式

根据这两个关系式，当带状线的尺寸w、b 和t 已知时，即可确定待定的参数ξ 和k。这样，式（12）的具体表示式也就确定了；反之，当给定了ξ 和k 时，也可以求出所需要的尺寸w、b 和t。

当带状线中心导体的厚度t 为零时，从附图3.1-3 可以看出，在z 平面上应有D 和F 均趋于E，相应地，在T 平面上应有-ξ 和ξ 均趋于0 点。而变换式（12）则变为

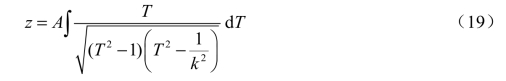
同样地，式（17）则变为

2.将复平面T 的上半平面变换为τ 复平面上的矩形域

这两个复平面之间的变换，以及两平面之间的对应点及线段，如附图3.1-3（b）和（c）所示。设带状线中心导体带的厚度t 为零。根据这个图，可以把T 平面与τ 平面上对应点的坐标，以及τ 平面上矩形域各顶点的顶角αn和等列表如下：

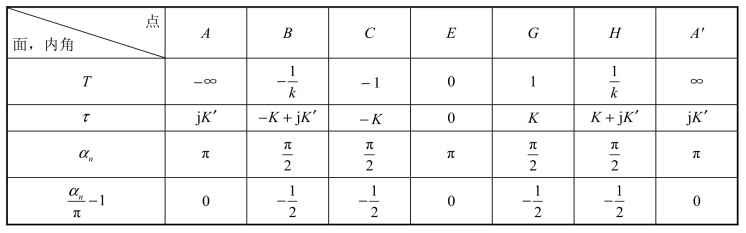
根据这个表和许瓦兹-克力斯托夫变换式可得

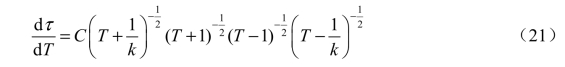
或写为

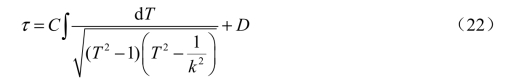
式中的C 和D 为待定的常数（实数或复数）。仿照前面确定式（12）中积分常数B 的方法，可以证明（证明从略）式（22）中的积分常数D 为零。

对于τ 平面上矩形域边界的尺寸，可以根据T 平面与τ 平面之间的对应点和对应线段，采用分段积分的方法来确定。在T 平面上，从E 到G（即从0 到1）的积分应等于τ 平面上与之相对应的从E 到G（即从0 到K）的积分，即

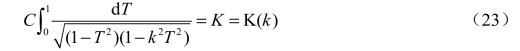
这个积分的上限为1，称为第一类完全椭圆积分，参变数k 称为该椭圆积分的模数。由该式可知，待定常数C=1。根据对称性可知，τ 平面上C 点的坐标为-K=-K（k）。类似地，在T平面上从G 到H（即从1 到1/k）的积分，应等于τ 平面上与之相对应的从G 到H（即从K到K +jK′）的积分，即

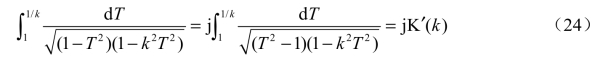
作积分变换，令

则K（k）′ 即可写为

显然，K（k）′=K′（k）。K（k′）也是第一类完全椭圆积分，k′称为椭圆积分的补模数。这样，τ平面上H 点的坐标为 K（k）+jK′（k），根据对称性，B 点的坐标为-K（k）+jK′（k）。矩形域ABCEGH 构成了一个电场是均匀的平板电容器，BAH 线段和CEG 线段表示电容器的两个极板，它们的宽度都是2K（k），长度都取为单位长度。由此可得该平板电容器的电容为

式中的εr是带状线中填充介质的相对介电常数，ε0是真空中的介电常数。如前所述，在进行保角变换时，只取了带状线横截面的1/2，因此带状线的全部电容应为

将此式代入式（2）中，则得带状线的特性阻抗为

对于电介质，μr≈1，则

以上利用保角变换法求出了带状线特性阻抗的表示式（3.1-2）。同样地，经过类似的推导过程即可求出耦合带状线、微带线和耦合微带线特性阻抗的表示式，限于篇幅，不再推导。在特性阻抗表示式中的K（k）和K′（k）表示椭圆积分的值（K 是椭圆积分的符号），其值取决于与带状线（或微带线）尺寸有关的参数k。若已知k，则K（k）和K′（k）以及特性阻抗也就确定了。式（23）和式（25）称为椭圆积分，一般地，根据被积函数和积分限的不同，可将其划分为多种类型，并冠以不同的称谓。椭圆积分的值无法用有限项的基本初等函数表示出来，但可用一个有无穷项的多项式之和来表示。因此在实际应用中，当已知k 时，可利用椭圆积分表或曲线图求出K（k）和K′（k）的值。

为了对K（k）和K′（k）有一具体的概念，消除其“抽象”感，下面对椭圆积分名称的由来和含义做一简单介绍。

在数学中，椭圆的弧长s 为

称为第二类椭圆积分，a 为椭圆的长半轴，，b 为椭圆的短半轴，φ 为所求弧长段与坐标轴之间的夹角，dφ 为其微分量。

椭圆的周长l 为

称为第二类完全椭圆积分，式中的K（k）可表示为

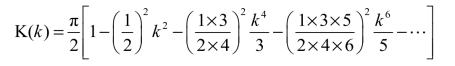
若给定了a 和b，也即给定了k，则K（k）即可求出（在一定精度范围内）。若a=b=R，则椭圆蜕变为圆，周长l=2πR，这正是圆的周长公式。

下面这个式子称为第一类完全椭圆积分

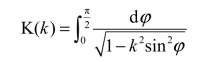
式中的K（k）可表示为

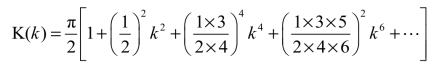
由以上所述可知，因为式（23）和式（25）的积分形式和积分值的表示式与求椭圆弧长或周长的表示式在形式上相似，故名“椭圆积分”。但是，这两种积分的积分变量和积分值的含义则完全不同，可见，“椭圆积分”只是一个借用的名称而已。需要指出的是，无论是实变函数还是复变函数，还有更为复杂的积分，虽然仍沿用“椭圆积分”这一名称，但与求椭圆的弧长和周长毫不相干。椭圆函数及其积分是数学中的一个分支，如有需要，读者可参阅有关的专著。为了更好地理解当k 已知时即可求出K（k）和K′（k），特在附图3.1-4和附图3.1-5 中给出了第一类完全椭圆积分K（k）和K（k′）/K（k）=K′（k）/K（k）与模数k 以及与（1-k）的关系曲线，供参考。

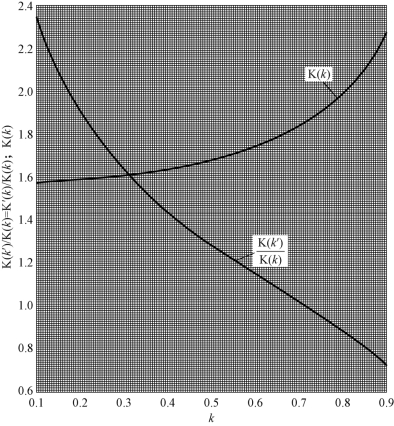
附图3.1-4 K（k）和K（k′）/K（k）与k 的关系图

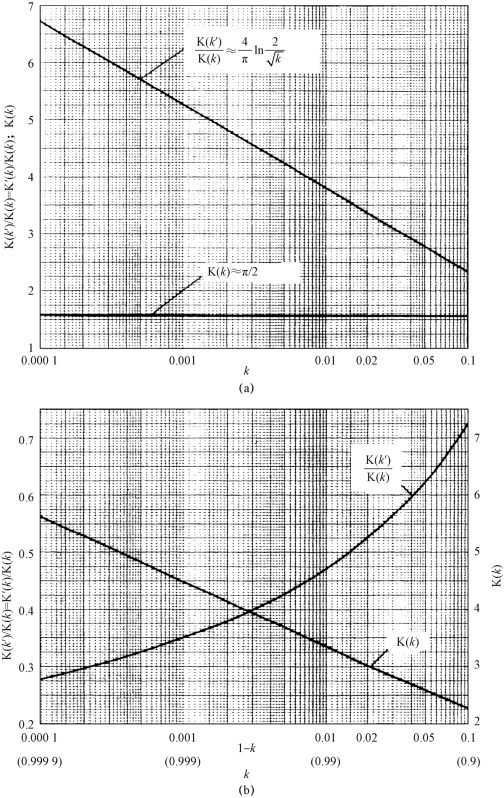
附图3.1-5 K（k）和K（k′）/K（k）与k 及1-k 关系图