
若微带线是被一种相对介电常数为εr的均匀介质所完全包围着,并把准TEM 模当作纯TEM 模看待,并设L 和C 分别为微带线单位长度上的电感和电容,则特性阻抗为

相速vp为

但是实际的微带线是含有介质和空气的混合介质系统,因此不能直接套用上面的公式求特性阻抗。为了求出实际的微带线的特性阻抗Zc和相速vp,而引入了等效相对介电常数的概念。如果微带线的结构形状和尺寸不变,当它被单一的空气介质所包围着时,其分布电容为C0。实际微带线是由空气和相对介电常数为εr的介质所填充,它的电容为C1,那么,等效相对介电常数εre的定义为

即是说,可以把实际的混合介质系统想象成是由单一的、均匀的、相对介电常数为εre的介质所构成的系统,它和实际的混合介质系统的特性阻抗和相速是完全一样的。这样,实际微带线的特性阻抗即可表示为

式中,![]() 为在同样形状和结构尺寸的情况下、填充介质全部是空气时微带线的特性阻抗,且
为在同样形状和结构尺寸的情况下、填充介质全部是空气时微带线的特性阻抗,且

由式(3.3-14)、式(3.3-15)和式(3.3-16)可知,所谓用准静态法求实际微带线的特性阻抗Zc,关键是求出静态场情况下的分布电容C0。求静态电容C0的方法有多种,其中常用的是保角变换法,下面只把用这种方法求出的结果写出来,以供查阅。
(一)导体带厚度为零时微带线特性阻抗的表示式
首先求空气介质时微带线的特性阻抗,然后再求充有其他介质时微带线的特性阻抗。
当导体带厚度t=0 时(这里为便于理论推导而做的假设,实际上不可能为零),空气介质微带线的特性阻抗![]() 的精确表示式为
的精确表示式为

式中,K(k′)和K(k)为第一类完全椭圆积分;k 和k′分别为其模数和补模数,它们是与微带线的结构尺寸有关的一个量。利用这个公式求![]() 是比较复杂的,因此通常可用由这个公式导出的求
是比较复杂的,因此通常可用由这个公式导出的求![]() 的近似公式。当w/h≤1 时,
的近似公式。当w/h≤1 时,![]() 为
为

当w/h≥1 时,![]() 为
为
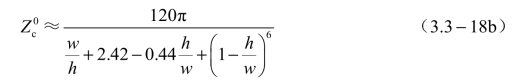
在0<w/h≤10 的范围内,上述公式的精确度可达±0.25%;当w/h>10 时,式(3.3-18b)的精确度约为±1%。
式(3.3-17)和式(3.3-18)是求![]() 的精确公式和由精确公式导出的近似公式。若导体带宽度w≫h,则计算
的精确公式和由精确公式导出的近似公式。若导体带宽度w≫h,则计算![]() 的另一近似公式为
的另一近似公式为
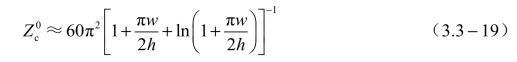
这个公式精确度差些,若要求稍微更精确些的计算,可采用下列的近似公式,即
 (www.zuozong.com)
(www.zuozong.com)
为了求出填充其他介质时微带线的特性阻抗Zc,还应知道等效相对介电常数εre。略去求εre的推导过程,而只把它的表示式写在下面,即
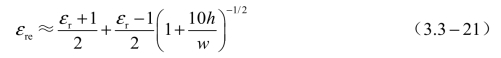
有时也可把εre写成下列形式,即
![]()
式中

称为填充系数,它表示εr>1 的介质的填充程度,当q=0 时,εre=1,表示微带中填充的全部是空气介质;当q=1 时,εre=εr,表示微带线全被相对介电常数为εr的介质包围着。利用这些公式,当已知w/h 时,利用式(3.3-15)就可求出特性阻抗Zc。
在实际中利用上述的一些公式求Zc是相当烦琐的,而且经常遇到的是给定了Zc和εr,需要求出的是w/h,这样,若利用上述公式就更为不便。因此,在一般工程计算中常利用曲线或查表格来求Zc,或由给定的Zc和εr来确定w/h。图3.3-3 是空气填充的微带线的特性阻抗![]() 、q 与w/h 之间的关系曲线。利用这个曲线进行计算是比较方便的,下面说明它的使用方法。
、q 与w/h 之间的关系曲线。利用这个曲线进行计算是比较方便的,下面说明它的使用方法。
若已给定w/h 和εr,需要求出的是微带线的特性阻抗Zc,其方法如下:首先在曲线图的纵坐标轴上找到w/h 的读数位置,过此点作平行于横坐标轴的直线,与![]() 的曲线和q 的曲线分别相交,相交点所对应的横坐标的读数即为
的曲线和q 的曲线分别相交,相交点所对应的横坐标的读数即为![]() 和q,然后利用式(3.3-22)和式(3.3-15)即可求微带线的特性阻抗Zc。
和q,然后利用式(3.3-22)和式(3.3-15)即可求微带线的特性阻抗Zc。
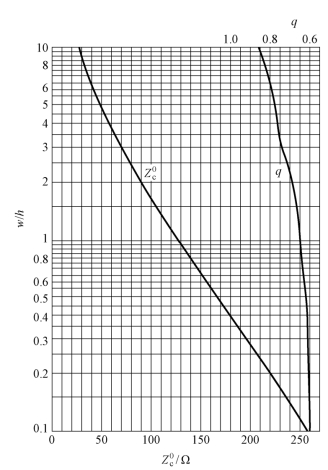
图3.3-3 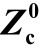 、q 与w /h 的关系曲线
、q 与w /h 的关系曲线
若已给定微带线的特性阻抗Zc和εr,需要求出的是w/h,其方法如下:利用式(3.3-15),即![]() ,先用εr代替εre求出
,先用εr代替εre求出![]() ,过横坐标上的
,过横坐标上的![]() 点作垂线,与图中
点作垂线,与图中![]() 的曲线相交,交点所对应的纵坐标即为w/h,过此w/h 点作平行于横坐标轴的直线,与图中的q 曲线相交,而求得q 值。由求得的q 值,利用式(3.3-22)求出εre,并利用式(3.3-15)求出新的
的曲线相交,交点所对应的纵坐标即为w/h,过此w/h 点作平行于横坐标轴的直线,与图中的q 曲线相交,而求得q 值。由求得的q 值,利用式(3.3-22)求出εre,并利用式(3.3-15)求出新的![]() 值,再根据这个新的
值,再根据这个新的![]() ,重复上述的计算步骤,又会得到一组w/h、q 和εre的值,以及
,重复上述的计算步骤,又会得到一组w/h、q 和εre的值,以及![]() 的值。不断地重复上述计算步骤,直到相邻两次计算出的εre值的相对误差小于1%为止,那么,根据最后一次求得的εre,即可求出
的值。不断地重复上述计算步骤,直到相邻两次计算出的εre值的相对误差小于1%为止,那么,根据最后一次求得的εre,即可求出![]() ,再根据
,再根据![]() ,在曲线图中得出w/h,若再假定h 已知,则w 即可求出。
,在曲线图中得出w/h,若再假定h 已知,则w 即可求出。
除上述的计算方法外,还有更为简便的方法,这就是直接查有关的表(见本章附录3.2),在这个表中给出了w/h、εre和Zc三者之间的对应数值,查找十分方便。对于表中未列出的数据,可采用内插法进行计算。
(二)导体带厚度不为零时微带线特性阻抗的表示式
前面讲的求微带线特性阻抗Zc的公式,是在假定导体带厚度t=0 的情况下求出的;而实际微带线中的t 不可能为零,而是具有一定的厚度。与t=0 时相比,t≠0 时导体带的边缘电容增加了,因此当这种增加效应不能忽略时,就不能直接利用前述的t=0 时的公式求Zc。但是,如果将t≠0 时边缘电容增加的影响等效为导体带的宽度增加了Δw,即把t≠0 时导体带的实际宽度w,用相当于t=0 时的等效宽度we来代替,那么,就可以利用前述的t=0 时的公式求Zc了。we、w 和Δw 之间的关系为
![]()
式中的Δw 可利用下面的一些公式计算。
当![]()
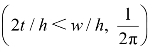 及时
及时
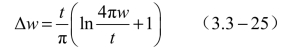
当![]() 时
时
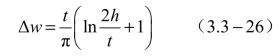
另外,也可以利用如图3.3-4所示的曲线求出Δw。
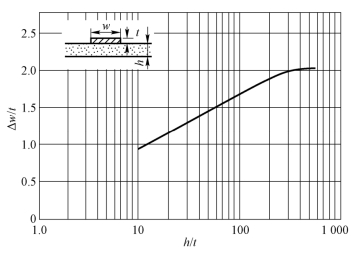
图3.3-4 Δw/t 与h/t 的关系曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




