矩形波导管中电磁波传输特性分析

在2.3 节中，对于一般规则波导中导行波的传播特性已做了较详细的讨论，并导出了有关的表示式。现在，我们以此为基础，具体地讨论矩形波导中电磁波的传输特性，内容包括：截止波长和截止频率；导波波长和相移常数；相速和群速；波型阻抗；传输功率；损耗和衰减。

（一）截止波长和截止频率

根据式（2.4-21）和式（2.4-27）可知，在矩形波导管中，TMmn和TEmn模的截止波数Kc的表示式是相同的，即

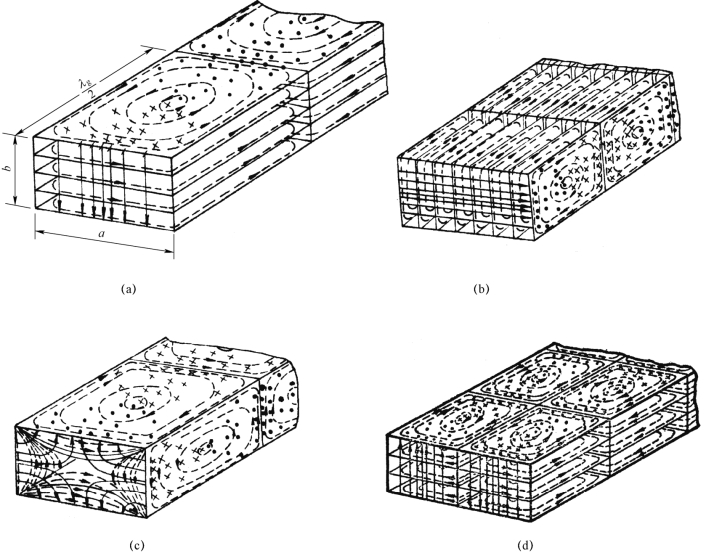
图2.4-4 矩形波导中TE 模场结构的立体图

（a）TE10；（b）TE01；（c）TE11；（d）TE20

由此式得出相应的截止波长λc为

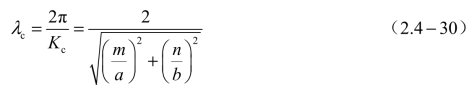
由此可知，Kc和λc是波导横截面尺寸和模式的函数；而且，当m 和n 均不为零时，TMmn和TEmn具有相同的Kc和λc。对于这种Kc或λc相同，但模（场结构）不相同的情况，称为模的简并现象。在矩形波导管中，因为分别与TE0n和TEm0相对应的TM0n和TMm0这两种模并不存在，所以TE0n和TEm0是非简并模，其余的TEmn和TMmn（m，n≠0）都存在着简并模。若a=b，则TEmn、TEnm、TMmn和TMnm是简并模；若a=2b，则TE01与TE20，TE02与TE40，TE50、TE32与TM32是简并模。从后面讲述的内容中将会看到，简并模的相速、群速和导波波长是相同的。

TMmn和TEmn模截止频率 fc的表示式是相同的，即

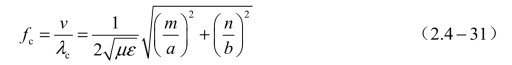
式中，电磁波的速度v 如式（2.3-35）所示。fc不仅与波导横截面尺寸、模式有关，而且还与波导中填充介质的参数μ 和ε 有关。工作波长λ 的表示式为

f 是工作频率。电磁波在矩形波导中的传播条件为λ＜λc或f＞fc。由上面的公式可知，虽然λc与介质的参数μ 和ε 无关，但在应用λ＜λc这个传输条件时，则应注意到是与介质参数有关的量。

一般地讲，不同的模，其截止波长是不相同的，其中最低次的模称为主模，而其他的模（m 和n 较大、截止波长较短、截止频率较高的模）则称为高次模。正如在前面讨论TMmn和TEmn模时曾指出的那样，在矩形波导中（当a＞b 时）最低次的TE 模是TE10，最低次的TM模是TM11，而且，TE10的λc大于TM11的λc，因此，矩形波导中的主模是TE10。当把矩形波导作为传输系统时，通常都采用主模TE10，并抑制高次模的传输，即所谓的单模传输，也就是说，在一定频率范围内，波导的工作模式是TE10。它的截止波长为2a，且与b 无关，而且在给定的频率范围内，可使波导横截面的尺寸最小，或者说，当尺寸给定时，能得到较宽的频率范围。TE10模的场结构简单、稳定、易激励、衰减小，在满足关系式

的情况下，就能够抑制高次模，能在较宽的频率范围内得到单模传输。在实际选取波导横截面的尺寸时，不但要保证单模传输，而且还要求能够承受一定的传输功率，并具有较小的功率损耗。

因此，为了兼顾这些要求，通常可以按下面的关系式来选取波导横截面的尺寸：

若采用多模传输，由于不同模式的相速、群速、导波波长、波型阻抗和场结构都不相同，不同模之间会产生相互干涉，场结构不稳定，负载与波导的匹配十分困难，使驻波比加大，从而使信息在传输过程中发生畸变和失真；而且，在模式的激励和信息的接收等方面都比单模时要复杂，此外，多模传输时，波导管的横向尺寸比单模传输时的横向尺寸要大，因此，一般不采用多模传输。但是，有时为了制作某种特殊用途的微波元（器）件（如多模馈源、喇叭天线，以及微波加热等），则可采用多模工作。

（二）导波波长和相移常数

根据式（2.3-40）和式（2.3-41）可知，TMmn和TEmn模的导波波长的表示式，以及它们的相移常数的表示式是相同的，分别为

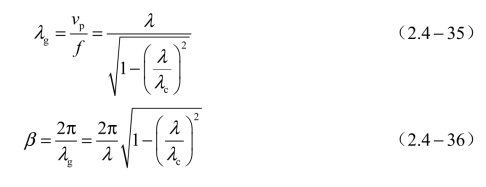
（三）相速和群速

根据式（2.3-39）和式（2.3-51）可知，TMmn和TEmn这两种模相速的表示式，以及它们的群速的表示式是相同的，分别为

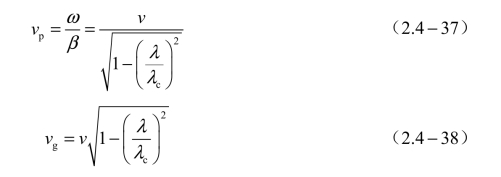
（四）波型阻抗

根据式（2.3-53）和式（2.3-54）可知，TMmn和TEmn模的波型阻抗Zw分别为

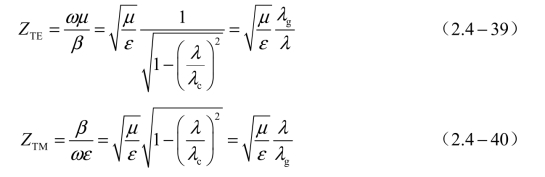
对于TE10、TE01、TE11和TM11等模式，其波型阻抗一般在200～800 Ω 之间。

（五）传输功率

在2.3 节中曾讨论了规则波导中功率的传输问题，并导出了传输功率的一般表示式。因为在实际应用波导来传输电磁波的能量时，通常并不是简单地计算出传输功率的值就可以了，而主要的是考虑波导能够传输（承受）的最大允许功率（极限功率），并称之为功率容量，所以，下面我们结合矩形波导的情况来讨论功率容量问题。功率容量与波导横截面的尺寸、工作波长、模式，以及波导中填充介质的击穿强度等因素有关，其计算方法是，首先求出传输功率与电场强度值的关系式，然后将介质所能承受的最大场强值（介质击穿强度）代入该关系式中，即可求出功率容量。现在以波导中传输的是TE10模为例，来导出功率容量的表示式。根据式（2.3-68）可知，在行波状态下，波导传输的功率为

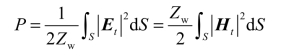
我们利用电场的横向分量来计算传输功率P。这样，对于TE10模，上式应为

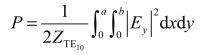
由式（2.4-28）可知

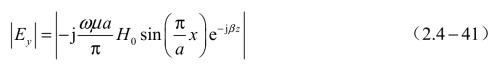
因为x=a/2 处有最大值，也最易击穿，所以为了避免击穿，应有下列关系式：

式中的 Ebr是波导中填充介质的击穿强度。将此关系式代入式（2.4-41）中，在极限情况下，令

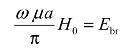
则

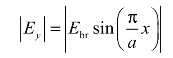
将此式代入式（2.4-41）中，即得到最大允许功率（极限功率）Pbr为(www.zuozong.com)

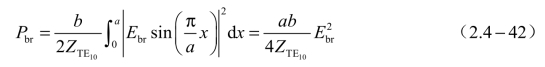
若波导中填充的介质为空气，则波型阻抗为

此时的最大允许功率Pbr为

空气的击穿强度 Ebr=30 kV/cm。

从上面的公式可以看出，对于TE10模，波导横截面尺寸越大，频率越高，极限功率也越大；但是，当f 趋于fc（或λ 趋于λc）时，极限功率趋于零。

以上所讨论的是行波状态时的情况，即波导中没有反射波存在的情况，若波导中有反射波存在，呈行驻波状态时，极限功率则由Pbr下降为 Pbr′，两者的关系为

式中的S 为驻波比。实际上，除了上面讲过的影响极限功率的几种因素之外，还有其他一些因素，如介质比较潮湿、波导壁内表面不清洁和波导内存在的任何不均匀性等因素，都会进一步降低极限功率。因此，在用波导传输较大的功率时，应留有一定的余地。

以上所讨论的是波导传输TE10模时的情况，至于传输其他模时极限功率的计算方法，与此相类似，故不再讨论。

（六）损耗和衰减

在实际中使用的波导，无论采用的是何种良导体和填充的是何种介质，总是存在着由波导壁内表面和填充介质所引起的热损耗，这必然会造成电磁波能量（或模值）的衰减。现在以波导中传输的是TE10模为例，来导出导体衰减常数αc和介质衰减常数αd的表示式。

1.αc的计算

根据式（2.3-80）知

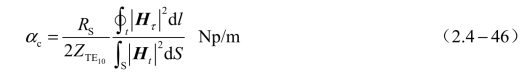
TE10模的磁场只有Hx和Hz，对波导壁内表面而言，它们是磁场的切向分量，它们的模值分别为

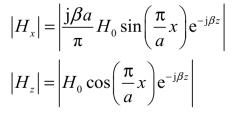
则

式中

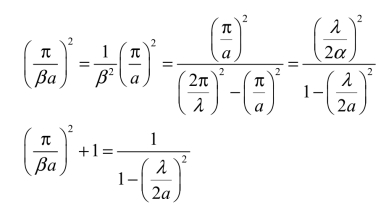
因此

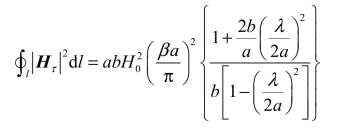
对于矩形波导的横截面而言，TE10模的横向磁场就是Hx，因此

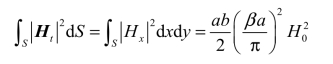
根据式（2.3-80）即得到αc的表示式为

由此式可知，当波导壁内表面的材料（其表面电阻率为RS）、波导中填充的介质，以及尺寸a给定时，则αc取决于尺寸b 和工作波长λ，而且b/a 越大，αc越小；若令dαc/dλ=0，即可求出αc为最小值时所对应的λ。如果填充的介质是空气，则αc的表示式为

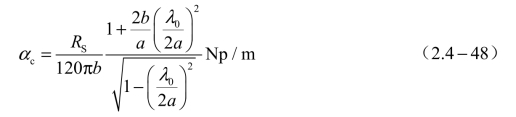
式中的λ0为电磁波在自由空间（近似地讲，在空气中）的波长。

2.αd的计算

根据式（2.3-87），αd的表示式为

或

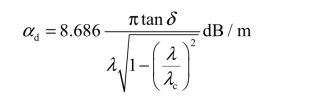
以上所讲的是波导中传输TE10模时导体衰减常数αc的计算。关于其他模αc的表示式，经过与上述的类似推导步骤，即可求得。现在略去推导步骤，只把其结果写出，供参考。

对于TEm0模，αc为

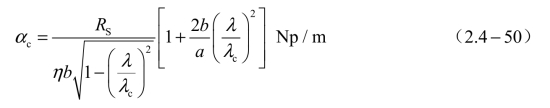
对于TEmn模（m，n≠0），αc为

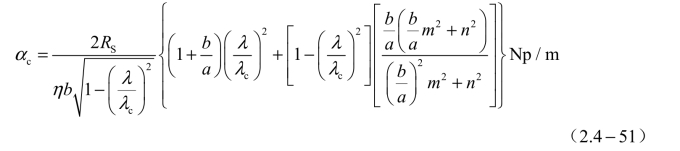
对于TMmn模，αc为

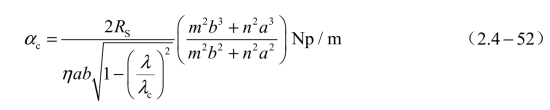
以上各式中的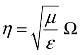，μ 和 ε 是波导中填充介质的磁导率和介电常数；对于空气介质。

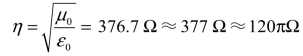作为传输系统而用的矩形波导，常用的模是TE10，为了保证单模传输，以及较小的损耗和较大的功率容量，波导横截面的尺寸和工作波长的选择，可以按照式（2.4-33）、式（2.4-34）进行计算。在满足这些要求的情况下，波导的尺寸应尽可能地小一些。目前一般矩形波导管横截面的尺寸已经标准化（参见本书附录空心金属波导管参数，各国标准化的尺寸略有不同），可根据要求选用。对于有特殊要求的矩形波导，则可根据情况自行设计。