使用阻抗圆图解决输入输出阻抗问题：实例分析

例1.5-1 一个特性阻抗 Zc为50 Ω 的传输线，已知线上某位置的输入阻抗 Zin=（50 +j47.4）Ω，试求该处的反射系数Γ。

解：归一化的阻抗为

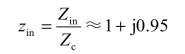
如图1.5-8所示，首先从圆图中找到r=1 和x=0.95 这两个圆的交点A，A 点即表示 zin≈1 +j0.95；然后从原点O至A 作连线OA，其长度即表示，OA 与实轴正方向之间的夹角Γφ 表示Γ 的相角。Γφ 可以根据B 点（OA 延长线与刻度圆的交点）处的相对波长数与正实轴处波长数之差来确定，即

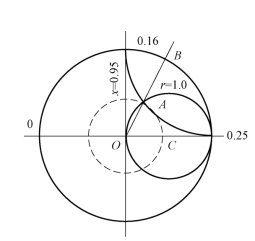
图1.5-8 例1.5-1 用图

另外，也可以从圆图上所标注的角度中直接求出Γφ。可以通过驻波比S 来计算，以OA 为半径，以O 点为圆心作圆交右半实轴于C 点，该点S 的读数（在数值上等于该点的r）为2.5，则

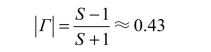
反射系数

例1.5-2 已知传输线的特性阻抗 Zc为50 Ω，终端负载阻抗Zl=（30 +j10）Ω，试求距终端负载λ/3 处的输入阻抗 Zin。

解：归一化的负载阻抗为

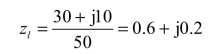
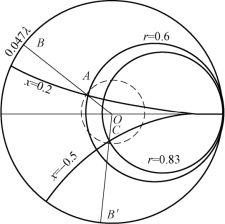
如图1.5-9所示，在圆图中找到zl=0.6 +j0.2的点A，从原点O 开始过A 作一直线，并延长此线与标有相对长度的刻度圆相交于B 点，从电压振幅值的波节点（即圆图的左半实轴上的点）算起，该点读数为0.047λ，将OB 顺时针方向旋转，落于处的B′点。以O 点为圆心、OA 为半径作一圆（等图），与OB′相交于C 点，该点的r=0.83，x=-0.5，即 zin=0.83-j0.5，则

例1.5-3 在特性阻抗 Zc为50 Ω 的传输线上测得驻波比S 为2.5，距终端负载0.2λ 处是电压振幅值的节点，试求终端负载 Zl。

解：电压节点处的归一化阻抗在数值上为K=1/S=1/2.5=0.4，即 zin=r=0.4。如图1.5-10所示，在圆图的左半实轴上找到与r=0.4相对应的点A，在等S 圆上将OA 逆时针方向旋转2β×0.2λ=（4π/5）rad，得线段OB，B 点处的归一化阻抗为zl=1.67-j1.04，则

(www.zuozong.com)

图1.5-9 例1.5-2 用图

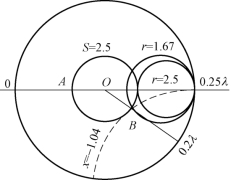
图1.5-10 例1.5-3 用图

例1.5-4 一传输线的特性阻抗 Zc为50 Ω，终端负载Zl=（100-j75）Ω，问在距终端多远处向负载方向看去的输入阻抗 Zin=50 +j X？

解：归一化的负载阻抗为

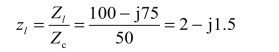
如图1.5-11所示，在圆图上找到与 zl对应的点A，对应的相对波长数为0.291λ。需要求的归一化的输入阻抗为

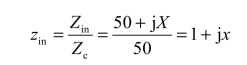
图1.5-11 例1.5-4 用图

可见，zin一定在r=1 的电阻圆上。以O 点为圆心、OA 为半径作一圆，与r=1 的圆相交于B 和C 两点，对应的相对波长数分别为0.329λ 和0.171λ。这样，就得到了两个位置：B 点和C 点。B 点距终端为

B 点处的输入阻抗为

C 点距终端为

C 点处的输入阻抗为