微分电路及矩形脉冲波形分析

图4.19 所示RC 电路中，如果输入信号是如图4.20（a）所示的矩形脉冲电压u1，脉冲电压的幅值为U、宽度为tp，电阻R 两端输出的电压为u2=uR，电压u2 的波形与电路的时间常数τ 有关。当输入脉冲宽度tp 一定时，改变τ 和tp 的比值，电容器充、放电的快慢就不同，输出电压u2 的波形也就不同，如图4.20（b）～（e）所示。

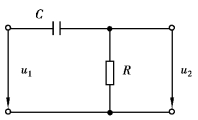
图4.19　微分电路

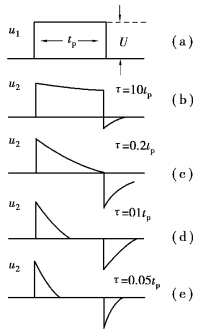
图4.20　不同τ 时的波形

下面具体分析以矩形脉冲为输入信号时，输出端电压uR 波形的形成过程，如图4.21所示。

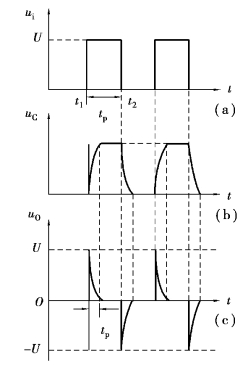
图4.21　RC 电路在矩形脉冲作用下的瞬变过程

在t=t1 时，脉冲由零跃变到U，相当于接通一个直流电压源，通过电阻R 对电容器C 进行充电。电容器两端电压uC 由零按指数规律上升，见式（4.12）。

uR 由U 按指数规律衰减，见式（4.14）。(www.zuozong.com)

如果电路的时间常数τ≪tp（实际上只需要使），如图4.21（b）所示，uC（t）很快由零增长到矩形波幅度值U。与此同时，u2（t）=uR（t）很快由幅值U 衰减到零值，这样在电阻两端输出一个正尖脉冲，如图4.21（c）所示。

在t=t2 瞬时，输入矩形脉冲信号由U 值跃变到零值，相当于输入端短路，于是电容器C经过电阻R 放电。由于τ≪tp，电容端电压uC（t）很快由U 衰减到零。同时，u2（t）=uR（t）由-U 衰减到零，这样在电阻两端就输出一个负尖脉冲。uC（t）和uR（t）波形如图4.21（b）、（c）所示。

这种输出尖脉冲反映了输入矩形脉冲的跃变部分，是矩形脉冲微分的结果，这种微分关系可以由以下推导看出。

由于τ≪tp，电容器充放电速度快，除了电容刚开始充电或放电的一段极短时间之外，u1=uC +u2≈uC。因而有

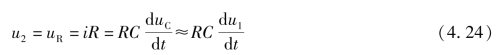
该式表明输出电压u2 近似地与输入电压u1 对时间的微分成正比。由此可见，RC 微分电路具有两个必备条件：

①τ（时间常数）≪tp（脉冲宽度）。

②从电阻元件R 两端输出电压。

在电子技术中，常应用微分电路把矩形脉冲变换为尖脉冲作为触发信号。