使用低通滤波器来抑制直流偏移问题

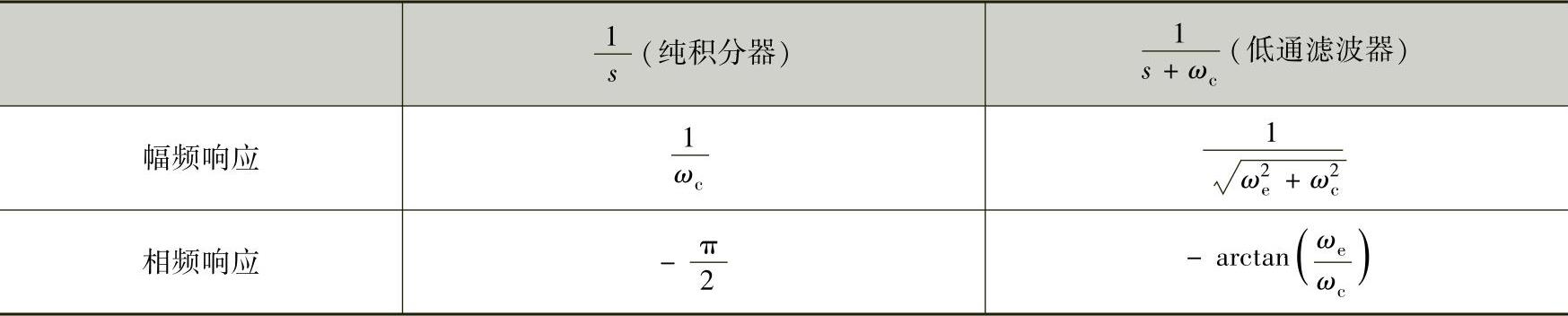
根据控制理论，一个控制系统的精度主要取决于反馈信号的精度，所以按定子磁链定向矢量控制的精度主要取决于磁链估计的精度。而磁链是由反电动势积分得到的，为了解决纯积分带来的积分器饱和及初值等问题，一般用一个截止频率较低的低通滤波器来代替纯积分器，这样可以抑制输入信号的直流偏移。但是，这又不可避免地引入了幅度误差和相位误差。纯积分和低通滤波幅频、相频响应比较见表5-1。

表5-1 纯积分和低通滤波幅频、相频响应比较

为了分析方便，将u-i模型写成如下形式：

式（5-5）在正弦稳态情况下，可以写成

这时

为了避免积分漂移问题，引入低通滤波器替代纯积分器，上述方程变为

式中，ω_c为所引入的一阶低通滤波器的上限截止频率。

从式（5-8）可以看出Ψ_s和Ψ′_s显然不相等，画出其矢量图如图5-2所示，从图中可以更加清楚地看到各个空间矢量之间的关系。

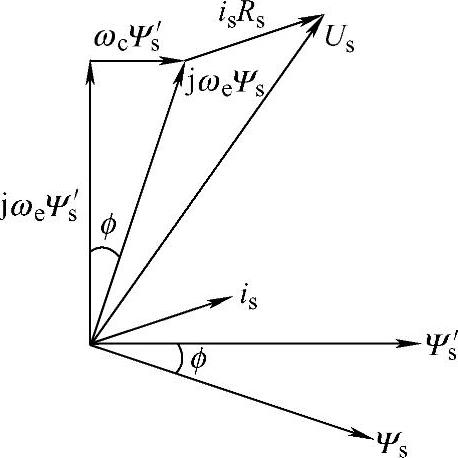
图5-2 采用低通滤波器的定子磁通与实际情况比较(www.zuozong.com)

从式（5-7）和式（5-8）可以得到

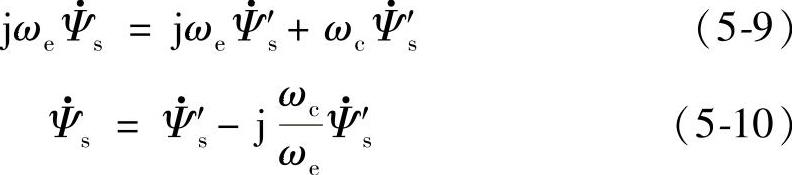
从式（5-10）可以看出，当ω_e/ω_c数值越大时，低通滤波器输出值越接近于纯积分器的定子磁链输出，误差越小。

将式（5-8）分子、分母同时乘以（ω_c-jω_e），可得

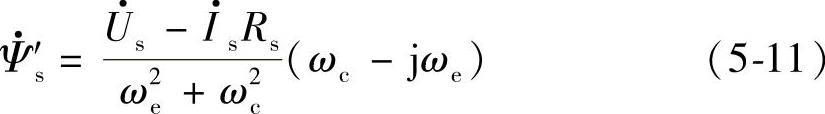
如果定义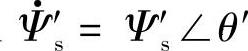、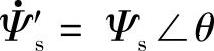，那么式（5-11）可以表达成为

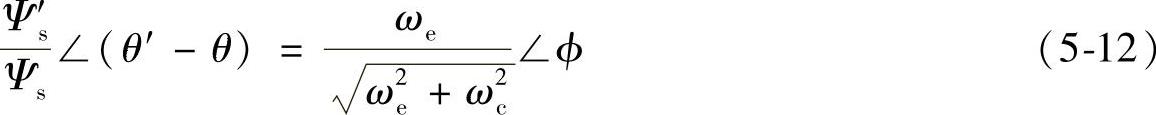
式中

当低通滤波器的上限截止频率等于同步频率时，从式（5-13）可以看出，这时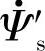和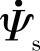之间的夹角ϕ等于π/4，幅度比为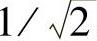。为了表达出在ω_c一定的情况下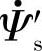，和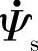之间比例关系随同步频率ω_e的变化情况，将在频域表达为

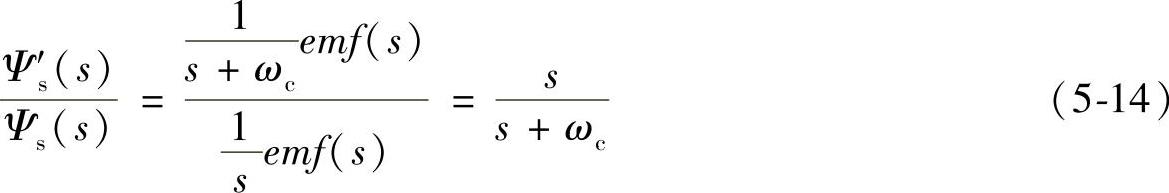
这样，可很容易地画出在ω_c=10rad/s时，ω_e从0.1Hz变化到100Hz时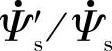的幅频和相频特性曲线。

从式（5-14）可以看出，低通滤波器截止频率ω_c的选择至关重要。ω_c选择得越低，低通滤波器造成的幅值和相位误差就越小，但与此同时，该低通滤波器对温度等因素引起的缓慢变化的输入信号或低频干扰信号的抑制作用会明显减弱。而ω_c选择得较高时，虽可以很好地抑制直流偏移和低频信号，但又会引入较大的磁链误差。显然，这是一对矛盾。

图5-3所示为一正弦信号作为纯积分器或低通滤波器输入信号时得到的输出的对比。其中，输入正弦信号峰值为10V，频率为20rad/s。图中，实线为纯积分器得到的输出信号，虚线为低通滤波器的输出。低通滤波器的上限截止频率ω_c设为10 rad/s。从图中两曲线可以看出，低通滤波器引入了明显的幅值和相位误差。