
构建基于谱域的图卷积神经网络,首先考虑如何从谱域定义的图上卷积。由卷积定理(函数卷积的傅里叶变换是函数傅里叶变换的乘积,即对于函数f与h,两者的卷积是其函数傅里叶变换的乘积)有
![]()
其中,f为待卷积函数,h为卷积核(根据需要设计),f*h为卷积结果。
可知,只要解决图上傅里叶变换的方法,就可以定义图上的卷积了,下面从传统的傅里叶变换开始逐步理解图上的傅里叶变换。
1.图上的傅里叶变换
(1)传统的傅里叶变换
传统的傅里叶变换定义为
![]()
其中,对于信号f(t)与基函数e-iωt的积分,为什么要用e-iωt作为基函数呢?从数学上看e-iωt是拉普拉斯算子的特征函数(满足特征方程),这样ω就和特征值有关了。
广义的特征方程定义为
![]()
其中A是一种变换,V是特征向量或者特征函数(无穷维的向量),λ是特征值。
e-iωt满足
![]()
当然e-iωt就是Δ的本征函数,ω与特征值密切相关。
由传统傅里叶变换可知,我们需要找到一个和e-iωt等价的一组基向量实现图上的傅里叶变换,为了寻找这组基向量,我们首先考虑图上的拉普拉斯算子。
(2)图上的拉普拉斯算子
①拉普拉斯算子的定义
拉普拉斯算子的定义如下:
![]()
拉普拉斯算子的含义很明确,它是所有非混合二阶偏导数的和。
②拉普拉斯算子在数字图像处理上的近似
图像是一种离散数据,那么拉普拉斯算子必然要进行离散化,先从导数说起:
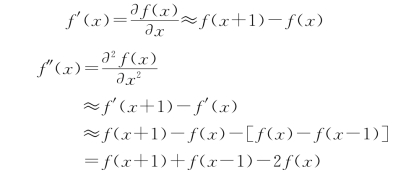
可以得出以下两个结论:
a.二阶导数近似等于其二阶差分;
b.二阶导数等于其在所有自由度上微扰之后获得的增益。
一维函数其自由度可理解为+1和-1两个方向。对于二维图像来说,则有4个自由度可以变化,即如果对f(x,y)处的像素进行扰动,其可以变为4种状态f(x+1,y),f(x-1,y),f(x,y+1),f(x,y-1)。当然,如果将对角线方向也认为是一个自由度的话,会再增加几种状态:f(x+1,y+1),f(x+1,y-1),f(x-1,y+1),f(x-1,y-1)。下面讨论第一种。
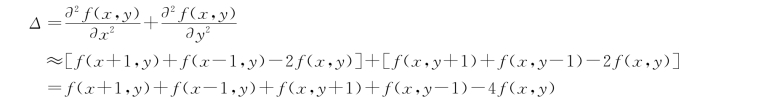
上式可以理解为,图像上某一点拉普拉斯算子的值即其进行扰动,时期变化到相邻像素后得到的增益。可以总结为拉普拉斯算子就是在所有自由度上进行微扰后获得的增益。
③拉普拉斯算子在图上的近似

其中,fi即函数f在节点i的值。类比图像中的f(x,y),即f在(x,y)处的值,对于任意节点i,对节点i进行微扰,它可能变为任意一个与它相邻的节点j∈Ni,其中Ni表示节点i的一阶邻域节点的集合。
对于图来说,从节点i变化到节点j的增益fj-fi是多少?最容易想到的就是和它们的边权相关,那就只有Aij了。
对于节点i来说,其变化的增益就是

如图4-22所示。
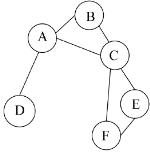
图4-22 图的拓扑图

•拉普拉斯矩阵⇔离散拉普拉斯算子。
•拉普拉斯矩阵的【特征向量U】⇔拉普拉斯算子的【本征函数e-iωt】。
④拉普拉斯矩阵(半正定、对称)
拉普拉斯矩阵的性质:
•有N个线性无关的特征向量。
•特征值非负。
•特征向量相互正交,即Q为正交矩阵。
下面给出拉普拉斯矩阵半正定性的证明。
证明:对于∀f∈RN,f≠0,有
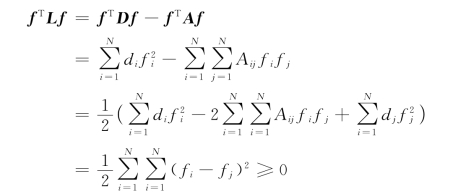
所以,拉普拉斯矩阵是半正定的。
(3)特征向量矩阵(一组基)
把拉普拉斯算子的特征函数变为图对应的拉普拉斯矩阵的特征向量。
①图上拉普拉斯算子的定义形式
先说图拉普拉斯算子的定义,有很多种,主要是以下2种。
a.L=D-A。
b.Lnor=D-1/2LD-1/2或者Lnor=D-1L。
其实就是一种,第二种是第一种的标准化(normalized)形式。
②求图拉普拉斯矩阵的特征向量
针对图拉普拉斯矩阵:
![]()
根据矩阵L的特征分解定义:将矩阵L分解为由特征值λ和特征向量u表示的矩阵之积。
a.求特征值和特征向量。λ为特征值,u为特征向量,则满足下式:
![]()
b.求特征分解。令L是一个N×N的方阵,且有N个线性无关的特征向量,这样L可以被分解为
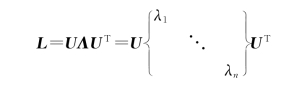
其中,U为图的拉普拉斯矩阵L的特征向量矩阵,且其第i列为L的特征向量ui,ui为列向量,U={u1,u2,…,un}。
设λ1≤λ2≤…≤λn为L的特征值,Λ=diag(λ1,λ2,…,λn)。
(4)图上的傅里叶变换
根据传统傅里叶的定义,得到图上的傅里叶变换:
①i为第i个顶点;
②λl为第l个特征值,ul为第l个特征向量;③f为待变换信号(向量),f^为其对应的傅里叶变换,f和f^与顶点i一一对应,即
![]()

即f在图上的傅里叶变换的矩阵形式为
![]()
逆变换形式为
![]()
为什么UT f就是对向量f的傅里叶变换,U f^就是对向量f的傅里叶逆变换呢?我们先来理解一下特征值和特征向量,从线性说起,一个线性变换可由一个矩阵乘法表示,一个空间坐标系可看作一个矩阵,那么这个坐标系就可由这个矩阵的所有特征向量表示,用图来表示的话,可以想象就是一个空间张开的各个坐标角度,这一组向量可以完全表示一个矩阵表示的空间的“特征”,而它们的特征值就表示了各个特征上的强度(可以想象成从各个角度上伸出的长短,越长的轴就越可以代表这个空间,它的“特征”就越强,或者说越显性,而短轴自然就成了隐性特征)。


其中,⊙表示哈达玛积(Hadamard product)。

3.图上的卷积核
(1)第一代GCN
卷积核:
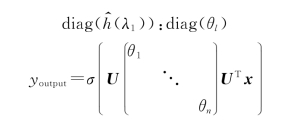
上式就是标准的第一代GCN中的layer了,其中σ(·)是激活函数,Θ=(θ1,θ2,…,θn)就跟三层神经网络中的weight一样是任意的自由参数,通过初始化赋值,然后利用误差反向传播进行调整,x就是图上对应于每个点的特征向量。
第一代GCN的缺点:有n个参数θn,计算量大。
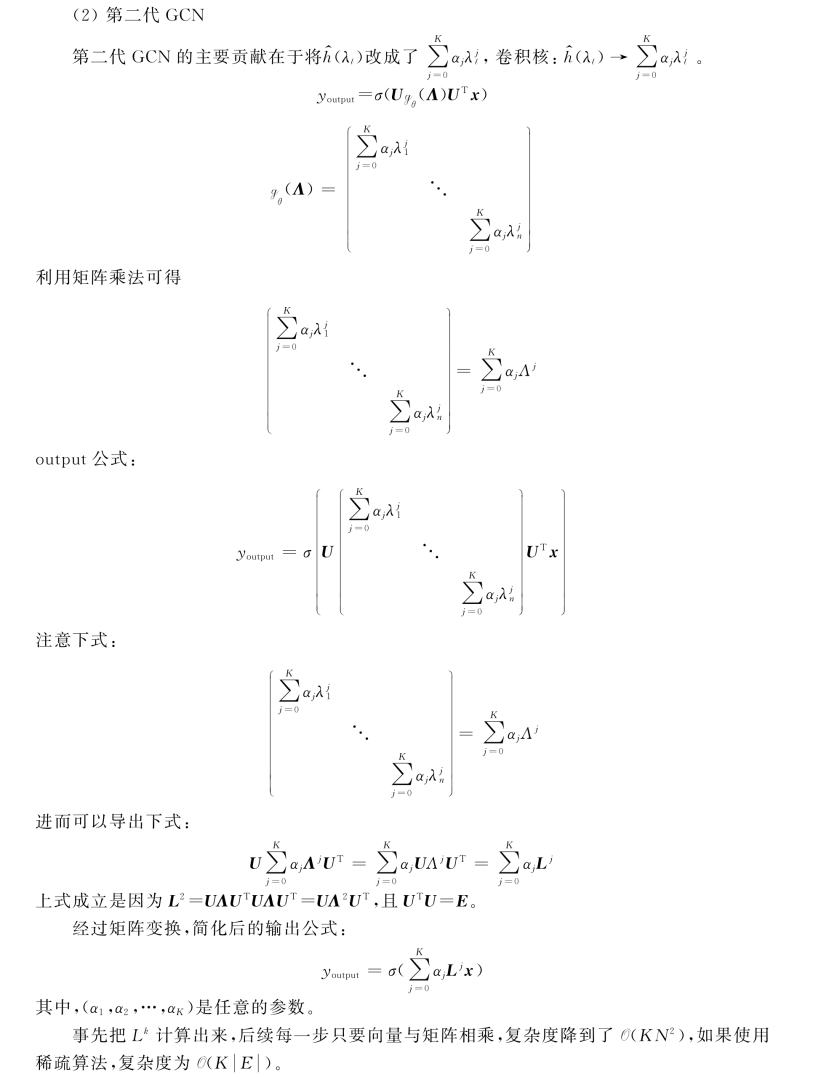
第二代GCN是如何引入空间局部性的呢?这里首先要讲到拉普拉斯矩阵的性质,对于一个拉普拉斯矩阵,如果节点dG(m,n)>s,则Lsm,n=0,其中,dG(m,n)为节点m和节点n的最短距离。因此第二代的卷积公式其实只使用了一个K-hot的邻域,即感受野为K。
有人提出了一种卷积核的设计方法,即gθ(Λ)可以用切比雪夫(Chebyshev)多项式Tk(x)到kth的截断展开来近似。
切比雪夫多项式:
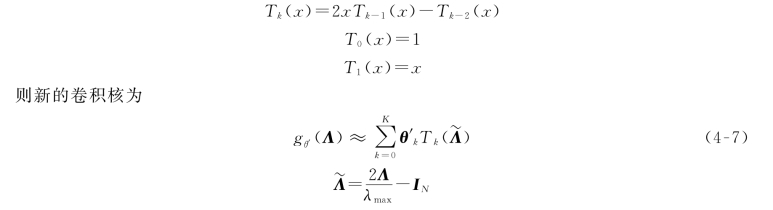
其中:λmax是L的最大特征值,是为了将其半径约束到[-1,1],防止连乘过程中产生爆炸;θ′∈RK是切比雪夫系数的向量。
根据切比雪夫多项式的性质,可以得到如下推导:
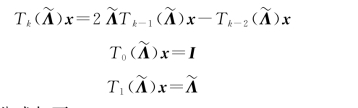
基于该卷积核,得到的卷积公式如下:
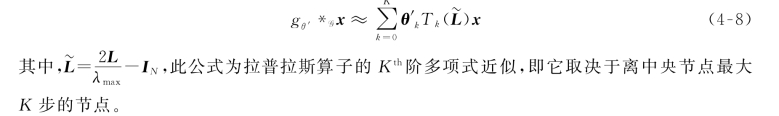
下面证明式(4-8)。要证式(4-8)需要下面两个基础推导。
①证明:
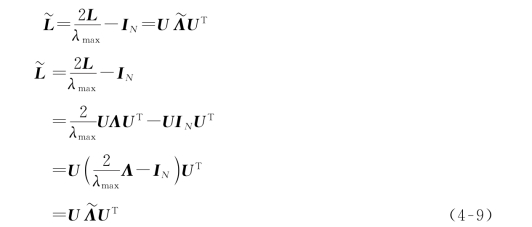
②命题:已知U为正交矩阵,L为对称矩阵,既满足
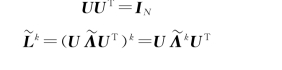
则有
![]()
证明:根据切比雪夫多项式的定义,已知
 (www.zuozong.com)
(www.zuozong.com)
•引入了空间局部性。
(3)第三代GCN
直到第二代GCN,基于谱的图卷积基本成形,第三代GCN改动不大,概括为两个点:
•令K=1,即每层卷积只考虑直接邻域,类似于CNN中3×3的卷积核;
•深度增加,宽度减少(深度学习的经验,深度>宽度)。
对于第二代GCN的公式
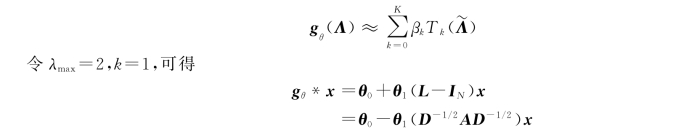
这里运用的是上面提过的归一化后的拉普拉斯矩阵:L=D-1/2(D-A)D-1/2=IND-1/2AD-1/2。其中,A为邻接矩阵,D为度矩阵。

•只考虑1-hop邻域,通过堆叠多层来增加感受野。
4.应用案例(一)——GCN
案例:图卷积神经网络。
本案例分析了Kipf和Welling 2017年介绍半监督图节点分类问题的论文,模型为两层GCN,论文下载地址为https://arxiv.org/pdf/1609.02907.pdf,有兴趣的读者可以下载阅读。
(1)卷积核
本案例的GCN采用了第三代卷积核,即
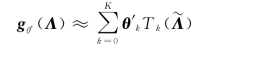
(2)层间递推关系
层间推导公式为

其中,yL代表已标注标签的节点集合。
(5)代码分析
以下代码为在Pytorch和Pytorch Geometric(Py G)框架下重现的GCN代码,大家如果感兴趣可以查看设计者提供的源代码,下载网址为https://github.com/tkipf/gcn。
①导入相应的包

②下载并处理数据集
本案例以Cora数据集为例:

其中,data中的内容如下。
•Data.edge_index=[2,10556]。COO稀疏存储格式,保存了图的所有边,若(i,j)∈E表示节点i到j的一条边,改变为图的第k条边,则Data.edge_index[0][k]=i,Data.edge_index[1][k]=j。
•Data.train_mask=[2708]。Data.train_mask[0~139]的值为Ture,其他值为Flase。
•Data.test_mask=[2708]。Data.train_mask[140~639]的值为Ture,其他值为Flase。
•Data.val_mask=[2708]。Data.train_mask[1708~2707]的值为Ture,其他值为Flase。
•Data.x=[2708,1433]。2 708个节点,每个节点的特征维度为1 433。
•Data.y=[2708]。每个节点的标注标签。
③定义卷积层


⑤将数据和模型复制到GPU并定义优化器

⑥定义模型训练函数

⑦定义模型测试函数

⑧训练并测试模型


图4-23 数据集Cora可视化结果
(6)实验结果
以Cora数据集为例,训练后模型利用TSNE对GCN的outputs进行可视化,结果如图4-23所示。
程序中训练迭代了200次,下面摘取了部分训练结果,本次训练结果最终的准确率为82.0%,经过多次训练,准确率在81.5%上下波动。

5.应用案例(二)——GMNN
案例:图马尔可夫神经网络(Graph Markov Neural Network,GMNN)。
图灵奖得主Bengio(图4-24)于2019年提出并开源了图马尔可夫神经网络。提出该网络的论文大量使用数学语言,语句简洁优美,值得反复阅读理解,对于理解图卷积神经网络及节点分类问题都很有帮助。结合了条件随机场和图神经网络模型的优势,模型基于节点特征对节点标签的联合分布进行建模,利用伪似然变分EM框架对条件随机场进行优化。在E-step中,使用GCN学习对象表示来进行标签预测。在M-step中,使用另一个GCN对节点标签的局部依赖关系进行建模。论文下载地址为https://arxiv.org/abs/1905.06214v1,有兴趣的读者可下载学习。

图4-24 图灵奖得主Bengio
(1)层间递推关系
GNN忽略了节点标签的依赖关系,关注于通过学习节点的有效特征表示预测未标注节点的标签。将标签的联合分布分解为
![]()
由上式可知GNN独立地推断每个节点的标签分布,对每一个节点n,GCN预测标签的方法可表示为

(2)GNN模型
E-step:qθ(yn|xV)=Cat(yn|softmax(Wθhθn))。
M-step:qθ(yn|yNB(n),xV)=Cat(yn|softmax(Wφhφn))。
(3)损失函数
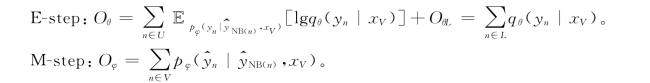
(4)代码分析
以下代码为在Pytorch和Pytorch Geometric(Py G)框架下重现的GMNN代码,并用GCN替代GNN模型,结果比设计者的运行结果的准确率高了将近1个百分点。大家如果感兴趣可以查看设计者提供的源代码,网址为https://github.com/Deep Graph Learning/GMNN,在设计者的源代码中,数据集加载部分处理较复杂,理解起来相对较困难。
①导入相关包

②创建ArgumentParser()对象


③加载import os

④定义模型输入和输出
⑤定义卷积层


⑥定义训练器




⑦定义网络模型
a.GNNq(用特征进行训练)

b.GNNp(用标签进行训练)

⑧处理GNNp和GNNq的初始化和更新
a.初始化init_q_data


b.更新update_p_data()

c.更新update_q_data()

⑨定义预训练函数

⑩定义训练测试函数
a.train_q

b.train_p

⑪训练并测试模型

(5)实验结果
在Cora数据集上测试,GCNq的准确率为84.2%左右,GCNp的准确率达到83.4%左右,略高于设计者使用GNN的运行结果。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




