入射电子和原子核的相互作用

当入射电子从原子核近距离经过时,由于受原子核库仑电场的作用,会引起入射电子被散射,这种散射过程可以分为弹性散射和非弹性散射两种情况。

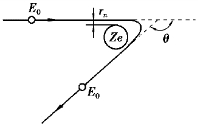
图4.2　卢瑟福散射模型

E0—入射电子的能量;θ—散射角

1)卢瑟福散射和弹性散射电子

如果入射电子与原子核相互作用遵守库仑定律,则电子在库仑势作用下发生散射,散射后电子的能量并不改变,这种散射即弹性散射,其运动轨迹将以一定的散射角θ偏离原来的入射方向。(图4.2)

这种散射称为卢瑟福散射(Rutherford scattering),相应被散射的入射电子称为弹性散射电子。理论分析表明,弹性散射电子的散射角θ可以用如下公式来确定:

式中,E0——入射电子的能量;

Z——原子序数;

e——电子电荷;(www.zuozong.com)

rn——入射电子轨迹到原子核距离。

由此可见,原子序数越大,电子能量越小,入射轨迹距核越近,则散射角越大。在电子显微分析技术中,弹性散射电子是电子衍射及其成像的物理基础。

2)非弹性散射和韧致辐射

如果入射电子和原子核发生非弹性散射,则入射电子将连续地损失其能量,这种能量损失除了以热的形式释放出来外,也可能以光量子(X射线)的形式释放出,并有如下关系

式中,ΔE——非弹性散射的能量损失;

h——普朗克常数;

c——光速;

ν——X射线的频率;

λ——X射线的波长。

因为ΔE是一个连续变量,相应转变为X射线的波长也是连续可变的,结果发射出无特征波长的连续X射线,这种现象称为韧致辐射(bremsstrahlung)。