参数范数惩罚的作用与实现

通过相关的训练方法，我们往往可以找到无数个深度模型来准确描述训练集中数据特征到标签的映射关系，此时存在一个模型的选择问题。正如前文所说，泛化性能是深度网络好坏的主要衡量标准，所以人们一般希望选择的模型能够拥有较低的泛化误差。然而，由于测试数据无法提前利用，所以一个深度网络的泛化性能无法被准确测量。14世纪，哲学家奥卡姆的威廉（William of Occam）提出“如无必要，勿增实体”原理，即“简单有效原理”，后来被人们称为奥卡姆剃刀原理。该原理虽然起初是针对哲学问题提出的，但后来被广泛应用到数学、管理学等领域。在机器学习上，奥卡姆剃刀原理指出，在训练误差都差不多的情况下，应该选择最简单的模型。

选择简单模型的一个直接有效的方法是参数范数惩罚，即对目标函数J添加参数范数惩罚项Ω（θ），限定模型的学习能力。添加参数惩罚项后的目标函数可表述为

式中，α是权衡因子，用于权衡目标函数和参数惩罚项对于总损失的贡献。对于目标函数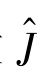的惩罚项，选择不同的范数会有不同的惩罚效果，常见的范数有L1范数和L2范数。在探究不同范数惩罚表现之前，需要说明一下，在深度神经网络中，一般只对每层神经元的权重参数进行范数惩罚，而不对神经元的偏置参数进行惩罚。因为在深度网络中，偏置参数的数量比权重参数少得多，即使不对其进行范数惩罚也不会导致过拟合。设向量w表示所有应受范数惩罚影响的权重参数。

（1）L1范数是指权值向量w各元素的绝对值之和，通常表示为

（2）L2范数是指权值向量w中各元素的平方和，然后求平方根，通常表示为

L1范数惩罚和L2范数惩罚的作用可简单归纳如下：

（1）L1范数惩罚可以产生稀疏权值矩阵，因此它可用于选择特征。

（2）L2范数惩罚可以防止模型过拟合。

8.1.1.1　L1范数惩罚

前文已经介绍，L1范数惩罚可以产生稀疏矩阵，进而可用于特征选择。当然，L1范数在一定程度上也能防止过拟合。在L1范数惩罚约束下的目标函数表示为

对式（8.2）求导，可得

式中，sign（w）是符号函数，其功能是取w中各元素的正负号。由此可以得到权重向量w的更新规则为

式（8.4）比原更新规则多了一项ηαsign（w）。当w为正时，sign（w）也为正，使得w在更新的同时逐渐变小；当w为负时，sign（w）也为负，使得w在更新的同时逐渐变大（朝着原点移动）。因此，L1范数惩罚的整体效果是让权重向量w靠近原点，使得网络中的权重尽可能为0，这也就相当于减小了网络复杂度，防止过拟合。

【注意】

当w等于0时，是不可导的，这时应当把ηαsign（w）项去掉，只按照原始的未经范数惩罚的方法更新w，所以可以规定sign（0）＝0。(www.zuozong.com)

式（8.2）可以改写成带约束条件下的优化问题，即

考虑二维的情况，约束项Ω＝是在二维平面上的一个正方形，它和原目标函数在二维平面上的示意如图8.1所示。图中的等值线是原目标函数J的等值线，黑色正方形是约束函数Ω的曲线。在图中，J的等值线与黑色正方形首次相交的位置即最优解，此交点的值是（w1，w2）＝（0，w）。因为L1约束项的图像有很多突出的角（在二维情况下有4个，在多维情况下更多），J与这些角接触的概率远大于与约束图像其他部位接触的概率；而在这些角上，会有很多权值为0，这就是L1范数惩罚可以产生稀疏模型，进而可以用于特征选择的原因。而约束项前面的系数α，可以控制约束项图像的大小。α越小，约束项图像越大；α越大，约束项图像就越小。

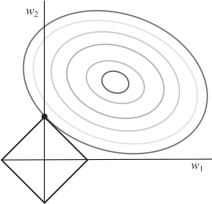
图8.1　L1范数惩罚平面示意（书后附彩插）

8.1.1.2　L2范数惩罚

L2范数惩罚是指对原来的目标函数加上参数的L2范数作为惩罚项。L2范数惩罚又称岭回归或者Tikhonov正则。在L2范数惩罚约束下的目标函数可以表示为

与之对应的梯度为

由此，可以得到参数更新规则为

式（8.8）进一步化简为

从式（8.9）可以看出，加入范数惩罚项的效果等效于先将之前的参数进行压缩，然后进行参数更新。

式（8.6）可以改写为带约束条件下的优化问题，即

考虑二维的情况，即参数w＝（w1，w2）。在二维参数平面上，原目标函数J的取值可以用一组等值线表示，而参数的L2范数约束是一个圆形，如图8.2所示。图中等值线和黑色的约束圆的交点即最优解的位置。约束圆的半径越大（对应式（8.6）的α越小），在L2范数惩罚下的目标函数最优解的位置就越靠近原目标函数最优解的位置；反之，约束圆的半径越小（对应式（8.6）的α越大），在L2范数惩罚下的目标函数的最优解的位置就越靠近原点。由此可见，范数惩罚项的作用是让权值尽可能小，最后构造一个所有参数都比较小的模型。因为参数值越小的模型越简单，能适应不同的数据集，也在一定程度上能避免过拟合现象的发生。可以设想，对于一个线性回归方程，若参数很大，那么只要数据发生微小偏移，就会对结果造成很大的影响；但如果参数足够小，数据偏移对结果造成的影响将减小许多。