理论推导：基于概率密度定义的C化简方法

理解了GAN的基本思想，就理解了整个生成对抗网络的基本过程与优化方法，但如果希望更加透彻地理解GAN，还需要知道更多的推导过程。本小节将证明当且仅当极小化极大博弈V（G，D）得到全局最优解D*和G*时，PG（x）＝Pdata（x）成立，即生成数据和真实数据同分布。为了证明这个结论，需要计算出极小化极大博弈V（G，D）的全局最优解D*和G*。

5.2.2.1　最优判别器

在极小化极大博弈的第1步中，给定生成器G，最大化V（D，G）而得到最优判别器D*。价值函数V（D，G）可表示为在x上积分的形式，即

此时，求积分的最大值可以转化为求被积函数的最大值，而求被积函数的最大值是为了求得最优判别器D*，因此不涉及判别器的项都可以看作常数项，G可以暂时看成常数，而V（G，D）可以看作关于D的函数，并且设D（x）＝y。在样本空间中，将真实的数据分布Pdata（x）设为a，生成的数据分布PG（x）设为b，于是，式（5.42）的内层被积函数可以简写为

如果a＋b≠0，就可以通过对式（5.43）求一阶导数的方式来求解最优的极值点，即

继续求表达式f（y）在驻点的二阶导数，可得

式中，a，b∈（0，1）。

由于一阶导数等于零、二阶导数小于零，因此可知为极大值。将a＝Pdata（x）、b＝PG（x）代入式（5.44），可得最优判别器为D*（x）＝y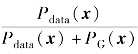＝。价值函数表达式可以表示为根据上面的推导过程可知，当D（x）＝Pdata/（Pdata＋PG）时，价值函数V（G，D）取到极大值。因为f（y）在定义域内有唯一的极大值，所以最优D*是唯一的。

5.2.2.2　最优生成器

GAN的目标是令PG（x）＝Pdata（x）。将这一等式代入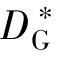的表达式，得到

这意味着判别器完全分辨不出Pdata（x）和PG（x），即判断样本来自Pdata（x）和PG（x）的概率都为0.5。那么可以得出结论，当且仅当＝Pdata（x））成立。下面对该结论进行证明。

令C（G）＝V（G，D），C（G）是关于G的函数，将与G无关的量视为常数。首先需要求出V（G，D）的全局最小值G*。当PG（x）＝Pdata（x）时，可以反向推出(www.zuozong.com)

该值是全局最小值的候选，因为它只有在PG（x）＝Pdata（x）时才出现。对任意一个G，将上一步求出的最优判别器D*代入C（G）＝V（G，D），可得

接下来，对C（G）进行化简，因为已知－log 4为全局最小候选值，所以希望构造某个值以使方程式中出现log 2。因此可以在每个积分中加（或减）log 2，并乘上概率密度。这是一个十分常见并且不会改变等式的数学证明技巧，因为本质上只是在方程加上了0。对C（G）化简，得根据概率密度的定义，PG（x）和Pdata（x）在各自的积分域上的积分等于1，即

此外，根据对数定义，可得

将式（5.51）和式（5.52）代入式（5.50），得到

可以发现，式（5.53）的两个积分都是KL散度的形式，得到

因为KL散度是非负的，所以候选值－log 4为C（G）的全局最小值。

对于KL（P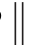 Q）而言，当且仅当P＝Q时，KL（P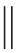Q）＝0。也就是说，当且仅当PG（x）＝Pdata（x）时，C（G）＝－log 4。综上可得，通过极小化极大博弈V（G，D）得到的最优解D*和G*可以使PG（x）＝Pdata（x），得到最优生成器G。

因为KL散度是非对称的，所以式（5.54）中的KL的左右两项是不能交换的，但如果加上另一项KL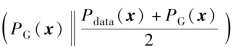，加和后的结果对于Pdata（x）和PG（x）来说就变成了对称的。这两项KL散度的和称为JS散度（Jenson－Shannon Divergence），即

式中，P和Q表示两个分布，且这两个分布的平均分布为M＝（P＋Q）/2。JS散度的取值范围为[0，log 2]。若两个分布P和Q完全没有交集，那么它们的JS散度值为log 2；若两个分布P和Q完全一样，那么它们的JS散度值为0。因此函数C（G）也可以根据JS散度的定义改写为

从JS散度的定义可知

与KL散度类似，当PG（x）＝Pdata（x）时，JSD（Pdata（x）PG（x））＝0。