
1.VHDL编程
(1)普通加法器
●半加器描述,具体设计如下:

●全加器中的或门描述,具体设计如下:

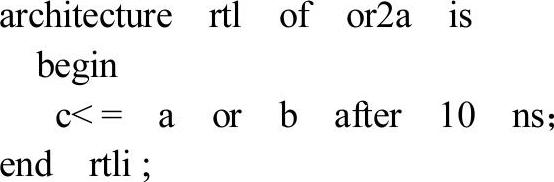
●1位二进制全加器顶层设计描述,具体设计如下:

在VHDL中,function语句中括号内的所有参数都是输入参数或称为输入信号。因此,在括号内指定端口方向的“in”可以省略。function的输入值由调用者复制到输入参数中,如果没有特别指定,在function语句中按常数处理。例如,以下加法器的VHDL程序描述。
●普通加法器。使用function语句实现,具体如下:


(2)级联加法器
以下的实例是用文本、图形结合输入方法设计,由两个并行的4位加法器级联而成的8位二进制加法器。VHDL和原理图输入方法的关系可以比作为高级语言和汇编语言的关系。VHDL的可移植性好,使用方便,但效率不如原理图输入;原理图输入的可控性好、效率高、比较直观,但设计大规模FPGA时显得很烦琐,移植性差。在真正的FPGA设计中,通常建议采用原理图和VHDL结合的方法来设计,在适合用原理图的地方用原理图,适合用VHDL的地方用VHDL,并没有强制性的规定。在短时间内,用自己最熟悉的工具设计出高效、稳定、符合设计要求的电路。
用层次设计概念,一般将一项设计任务分成若干模块,先规定每一模块的功能和各模块的接口,然后再将各模块进行编译生成.sym文件,最后利用图形输入法设计电路顶层文件,指定I/O管脚,编译生成.pof文件。
以下为设计的8位二进制加法器,它由两个并行的4位加法器级联而成。其中4位加法器的VHDL程序描述如下:
●4位加法器底层设计,具体如下:


在QuartllsⅡFile菜单中选择CreateSymbolFileforCurrentFile项,即可创建一个设计的符号。结果如图5-34所示。
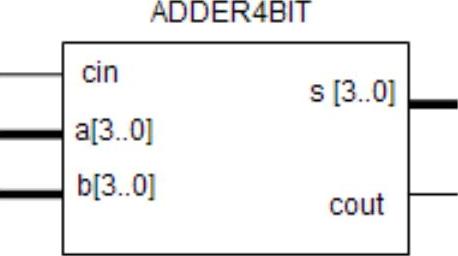
图5-34 4位加法器Symbol图
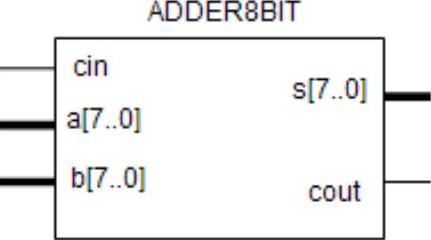
图5-35 8位加法器Symbol图
关于图5-34例化封装,设计完成具有一定的功能文件后,就相当于“制作”了该元件,可以把该元件当做底层元件,在以后的设计中调用,既可以文本调用,也可以图形调用。图形编辑顶层文件比较直观,且便于修改。这就需要对底层文件进行封装的考虑。
对于*.bdf的顶层文件,执行菜单File→Create Symbol File for Current File即可封装为元件。如果封装后又进行I/O管脚的修改,就需要重新进行封装,因为原来生成的Symbol不自动更新。
对于VHDL文件,进行第一次成功编译后,就自动生成Symbol。但是如果第一次成功编译后,又进行了I/O管脚的修改(port里面的in/out),即使再次编译成功,原来生成的Symbol也不自动更新,需要进行手工更新。
在图形设计顶层文件时,对使用的Symbol(元件)双击,可以进入该Symbol的底层文件。如果这时对该底层文件I/O管脚进行了修改,不仅要进行重新封装,而且在关闭该底层文件返回到顶层文件后,要选择该Symbol,执行菜单Symbol→Update Symbol,更新后要注意原来的连线是否正确。
根据图5-34所示的接口方式,在一个顶层设计中将以上各模块通过元件例化,连接成一个如图5-31所示的完整的设计实体。
编译成功后,还可以再生成一个例化元件,如图5-35所示。
图5-35所示的设计相当于如下VHDL程序描述。
●基于4位加法器的8位加法器,具体设计如下:

(3)流水线加法器
设计4位流水线加法器add4,只是在先前adder4bit的基础上增加一个寄存器,如图5-36所示。
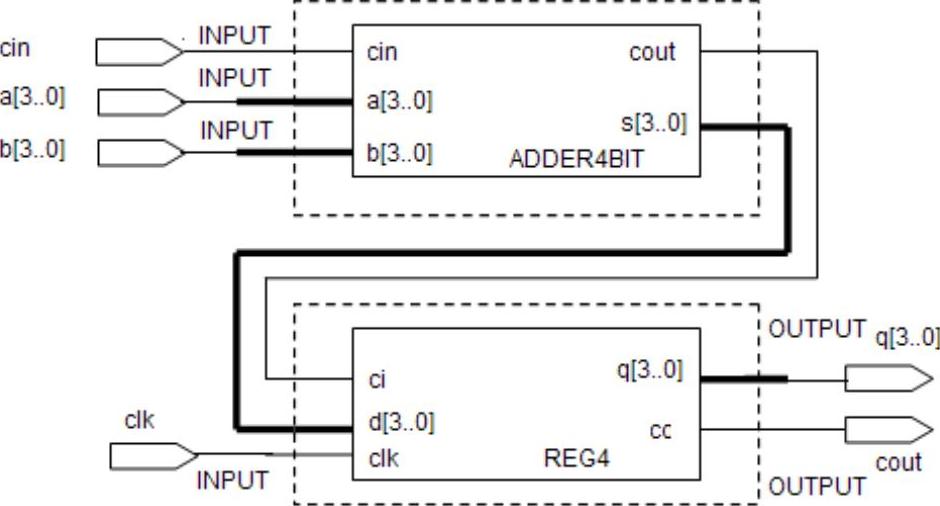
图5-36 4位流水线加法器
还可以级联成如图5-37所示的8位流水线加法器。该加法器由两个4位加法器组成,它们的输出寄存在REG中。功能块add4即4位流水线加法器,它的输出位“和”q及1位进位位(Cout)。两个4位加法器合并构成的8位流水线加法器。8位加法器的高位q[7..4]需要从低位进位才能求和。然而输入到加法器的高位数据与进位输入不是同时到达的,因为低位产生进位需要花费时间。设计中采用流水线技术就能保证高位数据与低位产生的进位输出信号同时出现在高位加法器的输入上。两个相加数的低位q[3..0]是在第一时钟周期相加的.而高位q[7..4]是在下一个时钟周期相加的,此时低位add4的输出被寄存起来。(www.zuozong.com)
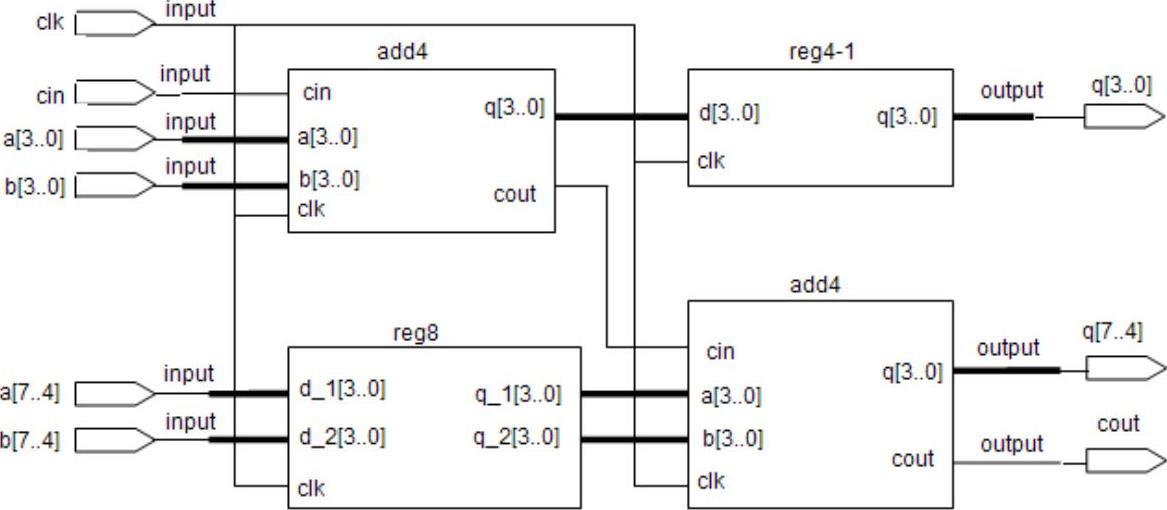
图5-37 8位流水线加法器
(4)乘法器
以下VHDL程序设计是基于“手工计算”的方法实现一个普通乘法器。
●方法1,普通乘法器,具体设计如下:


以下是用文本输入VHDL程序设计,采用移位相加的方法实现一个16*16位乘法器,移位相加乘法器实现起来很简单,它的设计思想是根据乘数的每一位是否为1进行计算。若为1,则将被乘数移位相加,这种方法硬件资源耗用较少。16*16位乘法器的VHDL程序设计如下。
●方法2,移位乘法器,具体设计如下:

(5)除法器
该电路的VHDL实现如下,对于该电路的程序实现主要是采用移位相减,即将除数移位到第一位不为零的位与被除数第一位不为零的数对齐,然后比较两数。若被除数比除数大,则两数相减,差放在被除数中,商的相应位置“1”:若被除数小于除数,则将除数左移一位,商的相应位置“0”:然后重复前边的过程,直到除法过程结束。
除法器设计编程如下:


2.时序仿真分析
1)半加器、1位全加器和用function语句实现的加法器分别如图5-38a、b、c所示,它们实现的功能都比较简单,这里就不再赘述。
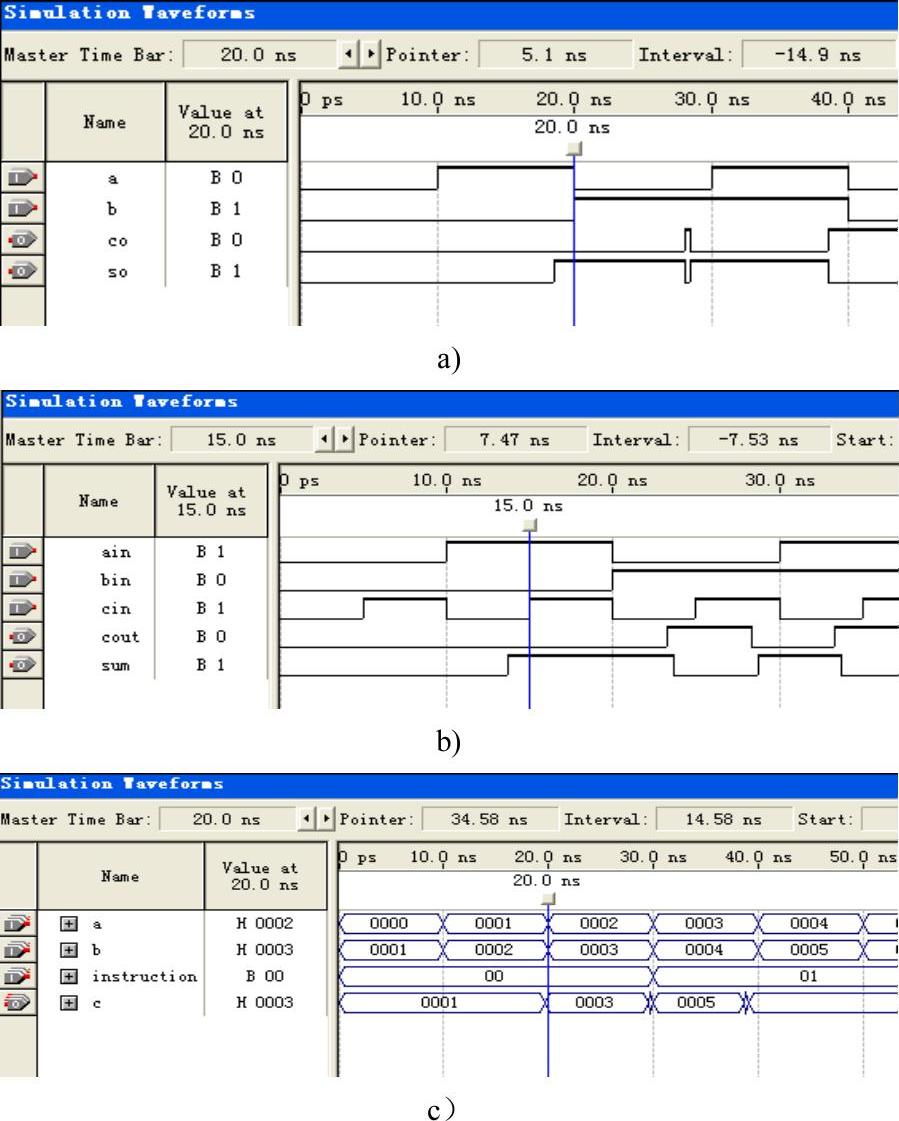
图5-38 普通加法器的仿真
a)半加器 b)1位全加器 c)function语句实现的加法器
2)底层4位二进制加法器及顶层8位二进制加法器的仿真如图5-39a、b、c所示,4位流水线加法器及8位流水线加法器的仿真分别如图5-40a、b所示,这些仿真都显示s=a+b,结果正确。
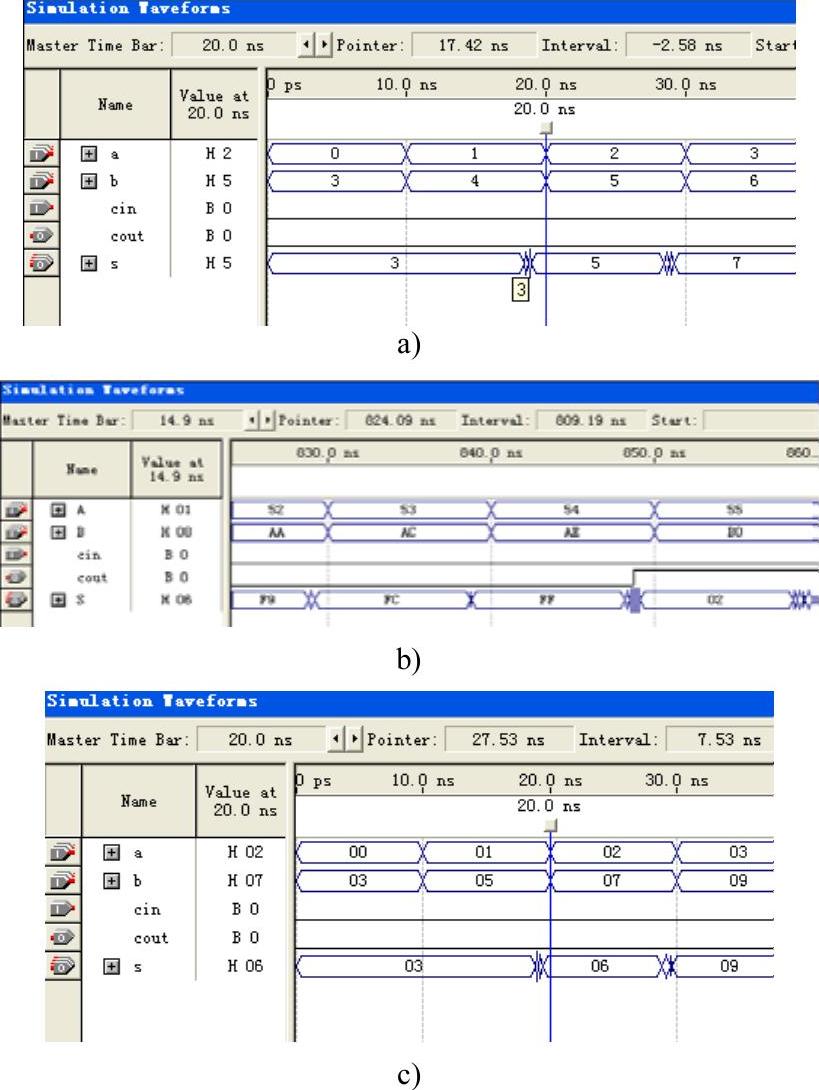
图5-39 级联加法器的仿真
a)4位二进制加法器 b)8位二进制加法器(图形级联) c)8位二进制加法器(VHDL级联)
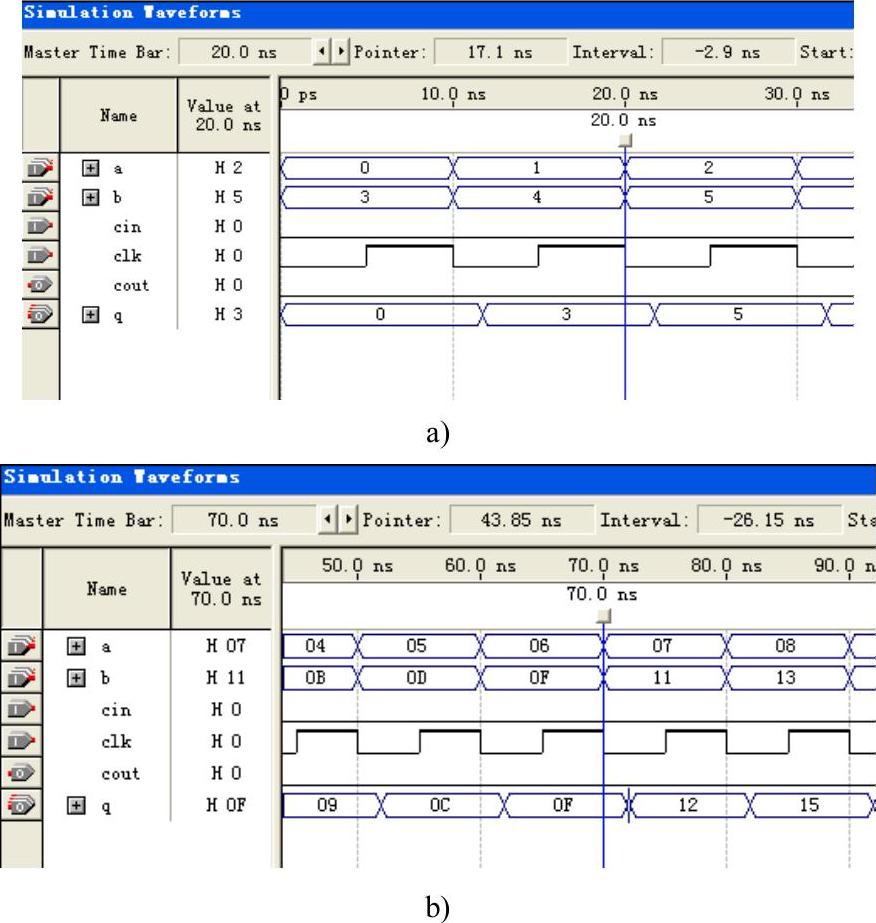
图5-40 流水线加法器的仿真
a)4位流水线加法器 b)8位流水线加法器
对比图5-40与图5-39的结果,可以发现流水线加法器的延时明显小于普通的多位加法器的延时,但这个代价是以使用更多的FPGA逻辑单元(LE)来换取的。
3)乘法器。基于“手工计算”的方法实现一个普通乘法器和移位实现的16位乘法器的仿真结果如图5-41a、b所示。这里需要说明的是,仿真需要设定比较合理的时间区域和输入信号频率。仿真时间区域不能太小,也不能太大;仿真输入信号频率不能太高,也不能小到与器件的延时相比拟。
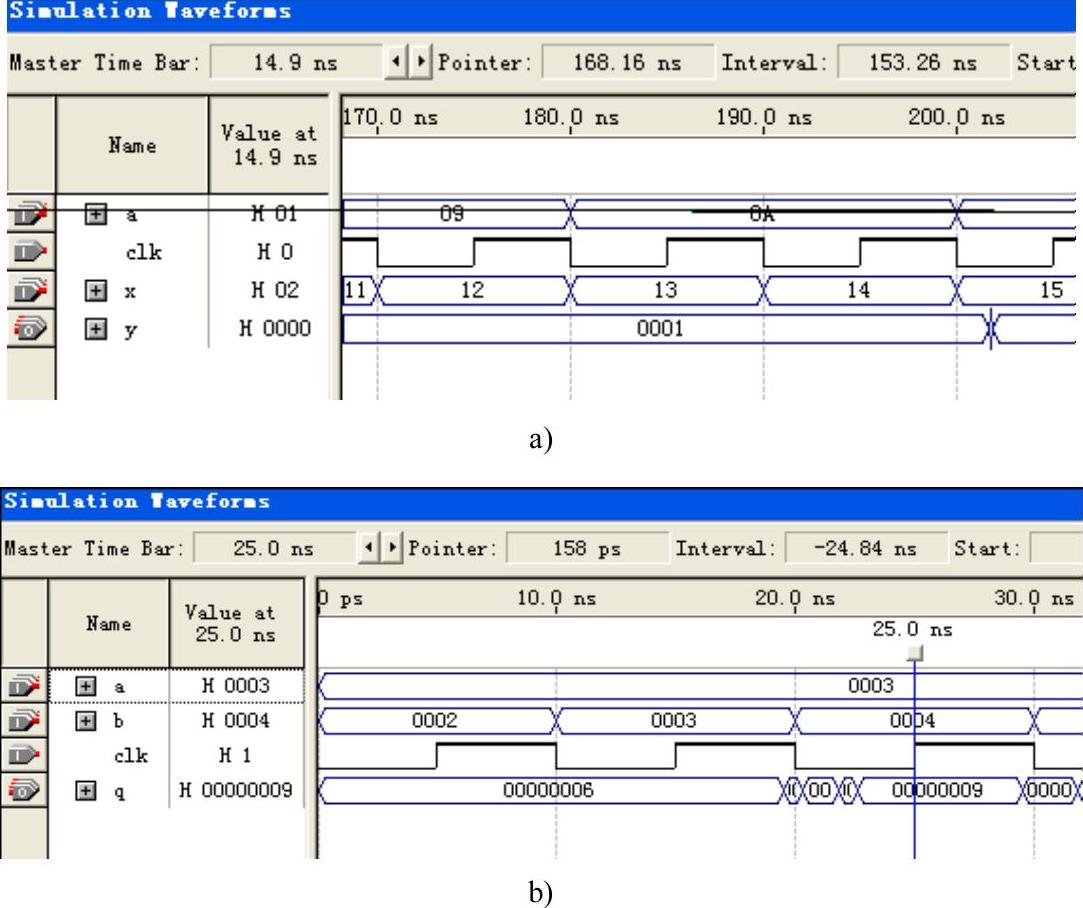
图5-41 乘法器的仿真
a)手工计算乘法器 b)16位移位乘法器
基于三重流水线方法实现的乘法器的仿真结果如图5-42所示。从图中可明显看到乘法的结果是正确的。“流水线”的作用:虽然单独完成一次运算需要5个时钟周期,但是当作业按照顺序准备号进入流水线操作时,就相当于一次运算值需要1个时钟周期。

图5-42 流水线乘法器的仿真结果
4)除法器的仿真结果如图5-43所示。
在计算机应用、仪器、仪表等领域的电子系统设计中,FPGA技术的含量正以惊人的速度增加。运算器是现代计算机中的一个重要组成部分,利用FPGA技术,能方便、灵活地设计出各种运算器。本节介绍了各种基于FPGA技术的运算器的设计与实现,并描述了采用VHDL和原理图方式设计完成多位加法器、乘法器、除法器的方法和步骤。
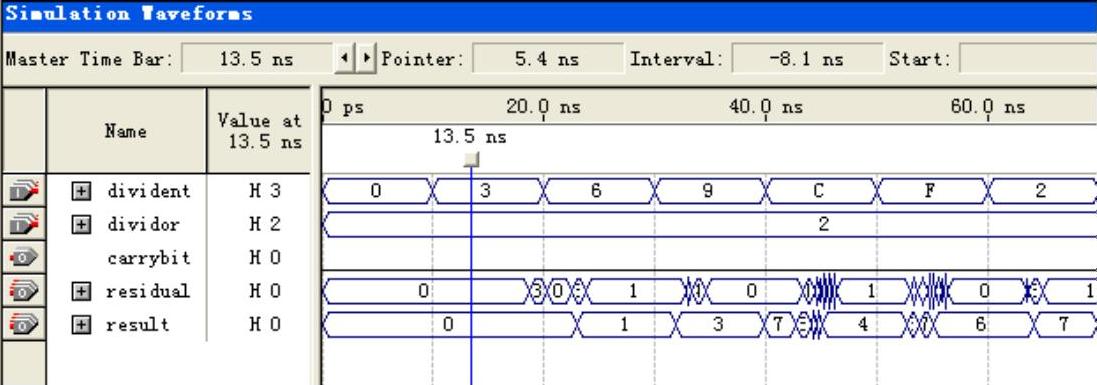
图5-43 除法器的仿真结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




