电流不连续模式与能量平衡法

表4.1给出了各种斩波器输出电压与开关时间之间的关系。这些关系只在电流连续模式下成立。

另一方面，根据电路的工作条件，持流电抗器的电流会存在变为零的区间，本节将主要说明这种电流不连续模式。升降压斩波器采用如图4.5所示电路，图4.6所示为不连续模式工作过程中它的动作波形。与连续模式的区别是电抗器电流i_L在到达一个周期T之前已经变为零，从而需要进行电流断续期间的推算，这会使得分析变得比较复杂，因此必须采用与之相称的方法。在这里，电路特性由从输入侧注入的能量与从输出侧释放的能量之间的平衡关系来决定，称为能量平衡法。以下将进行具体说明。

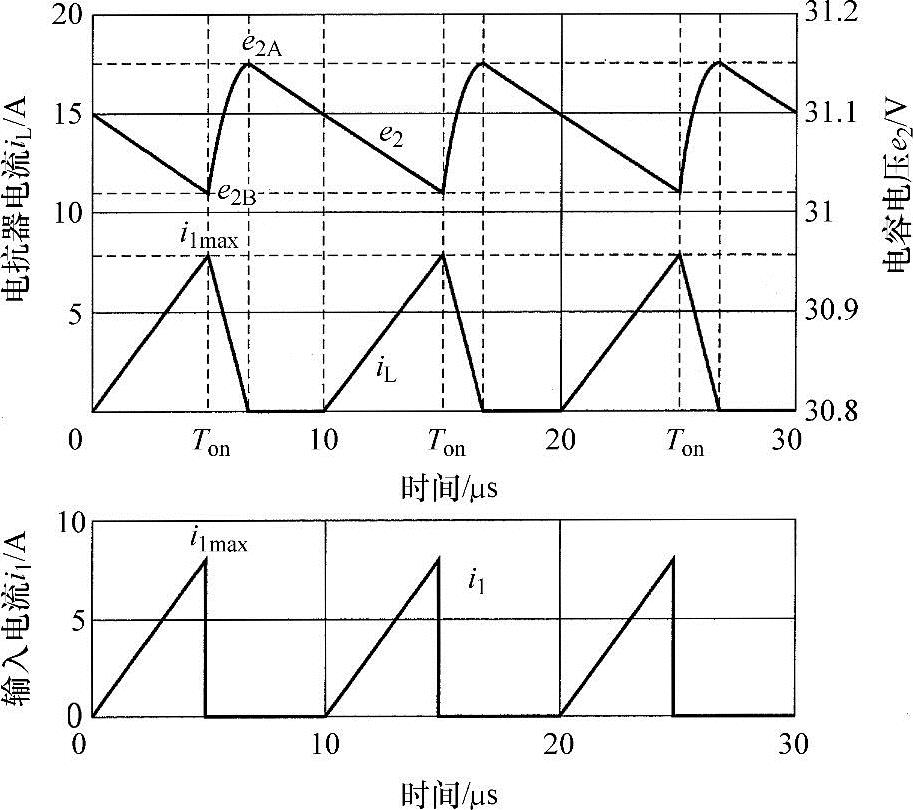
图4.6 电流不连续模式时升降压斩波器的仿真波形

（L=7.5μH，C=50μF，R=40Ω，T=10μs，D=0.5，E₁=12V）

图4.6所示为电流不连续模式时升降压斩波器的仿真波形，以此为基础进行说明。请注意右侧电压的坐标被放大了。t=0时刻SD变为导通状态（见图4.5a），持流电抗器电流i_L=i₁从零开始上升，电容电压e₂给负载放电的同时逐渐减少。T_on时刻一过，SD立即变为关断状态，持流电抗器给电容充电，同时也向负载放电。因此，e₂以二次曲线进行变化，图中电压从e_2B上升到e_2A，e_2A到达顶点时i_L=0。由于D_b的作用，持流电抗器从供电回路中脱离，电容为负载供电的同时，其电压持续下降。一个开关周期T=10μs结束时，SD会再次导通，如此循环往复动作。

在此考虑一个开关周期期间的能量流动情况。t=0时SD变为导通状态，i_L从零开始以（E₁/L）斜率上升，在T_on时刻达到最大值i_1max=E₁T_on/L。此时持流电抗器的能量是输入电源供给一个周期期间的能量，该能量在给电容充电的同时，也为负载电阻提供电能。过渡状态期间电容的平均能量W_C会有所增减，其变化部分由ΔW_C表示，各个开关周期中能量的收支情况如式（4.10）所示，其中，一个开关周期的负载端电压e₂的平均值为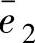，电容的平均能量为。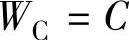

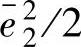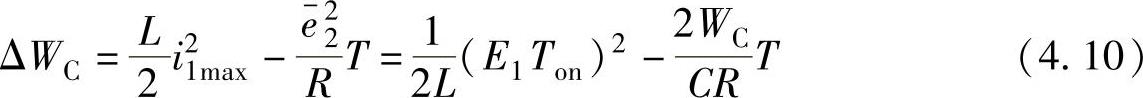
整理式（4.10），得到式（4.11）所示的微分方程式。这里没有直接给出平均状态量e-2，但可以间接求出电路的过渡过程。

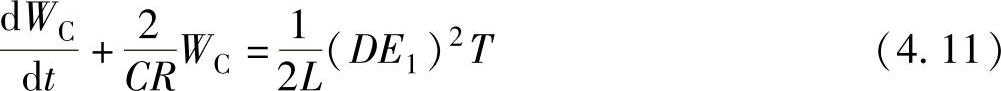
式（4.11）的暂态解可由数值计算得出，稳态解可由dW_C/dt=0求出，式（4.12）表示稳态解，其中，E₂和I₂是各种稳态情况下输出电压和电流的平均值，且I₂=E₂/R。

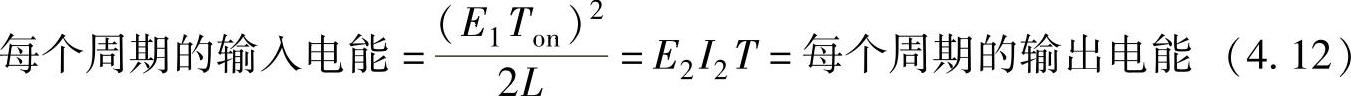
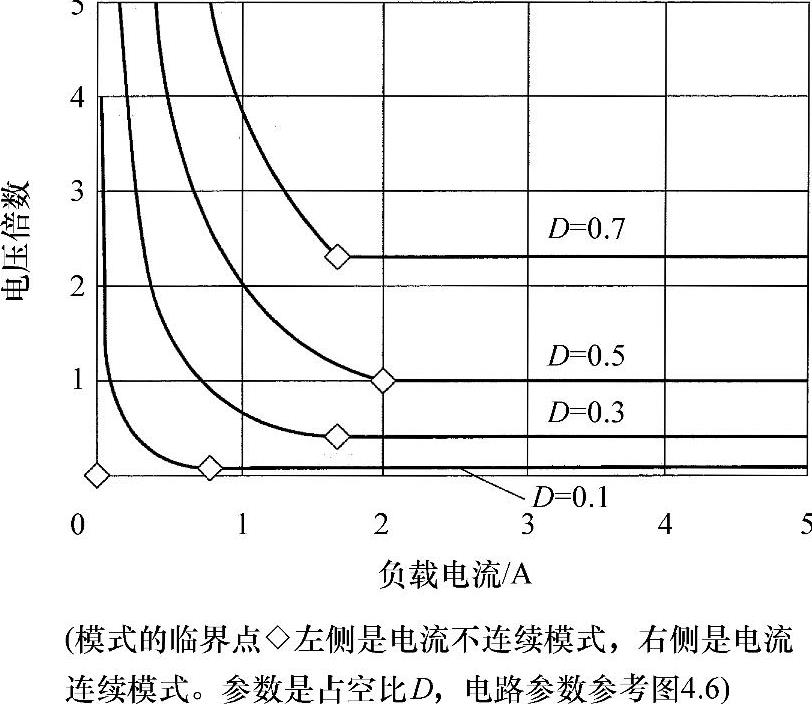
将以上的结果用于图4.6所示的仿真例子中，可以得到图4.7所示结果。图中◇记号表示电流不连续模式与连续模式的临界点，电流不连续模式时为双曲线形式，连续模式时变为恒电压特性。

(www.zuozong.com)

图4.7 升降压斩波器的电压倍数-输出电流特性

如上所述，在电流不连续模式下每个周期内输入一定的功率。因此，从图4.3a所示的负载端子B1-B2所看到的输出电源特性是恒功率电源（电压电流是双曲线特性）形式，这属于特殊情况。

例4.1

对于升压斩波器，计算电流不连续模式下的输出电压电流特性，并求出连续动作模式的临界动作点。

解 升压斩波器采用如图4.2所示的电路。由于即使在开关关断期间仍有电流通过电抗器，所以电源的电流波形与电抗器电流波形相同（参考图4.6）。在开关关断期间，除了电源电压参与给电容充电外，其余都与升降压斩波器相同。导通期间给电抗器注入的能量可由电流峰值i₁=（E₁/L）T_on推导出式（4.13）。

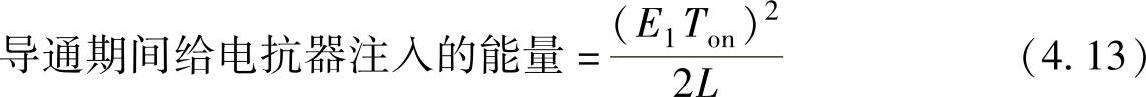
如果电容容量非常大，而输出电压E₂保持一定值，则关断期间电流变为零的时间为T_cond=Li₁（E₂-E₁），在此期间电源释放能量如式（4.14）所示。

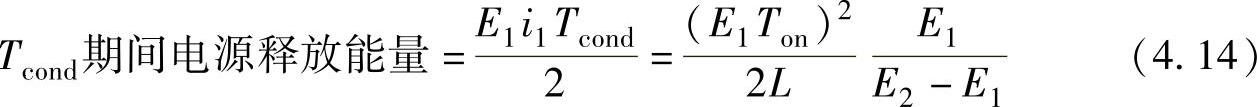
因此，周期T内电源释放的全部能量等于上述两者之和，它等于整个周期内的二次输出能量，所以得到式（4.15）。

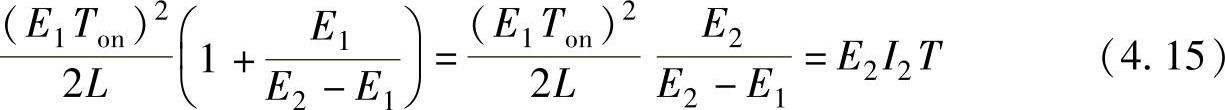
由此可以得出式（4.16）所示的电压电流特性。

式（4.16）右边第1项是升降压斩波器的稳态输出特性，因此，将升降压斩波器的特性偏移E₁，就得到了升压斩波器电流不连续模式下的输出特性。对于电流连续模式，两者间也存在同样的关系，升压斩波器的特性如图4.8所示，与升降压斩波器的特性相比，只有一倍电压倍数偏移。另外，两者的动作临界点也相同。