信息统计技术：描述统计和推断统计介绍

统计技术是在获取绩效考评信息过程中常用的第二种基本技术。从其功用来划分，统计技术大致有描述统计、推断统计、多元统计分析，下面介绍其中两种。

描述统计主要是就所要考评的对象特征行为进行全面的资料搜集，然后将所得的大量资料通过分类、累计、制表、绘图与简单运算等技术把它们加以整理、缩简、制成图表，或者就这些数据资料的分布特征（如集中趋势、离散趋势、相关程度等）计算出一些具有概括性的统计量，如平均数、标准差、相关系数等作为标志。借助这些概括性的数字，就可以从杂乱无章的资料中获取有意义的信息，便于对不同的考评对象作出比较，进行考评。

（1）数据的统计分类。数据的统计分类又称统计分组，这是对数据进行初步整理的第一步工作。分类时所依据的特征称为分类标志，按形式分为有性质标志与数量标志两种。也就是说，资料分类按形式划分有性质类别与数量类别两大类。如公司的职工可按性别或年龄来划分，前者属于性质类别形式，后者属于数量类别形式。

（2）统计表与频数分布表的编制。统计表是以表格的形式表达统计资料关系的重要工具。它可以化繁为简地反映表中各类事物的情况，便于分析、对比、计算与记忆。统计表通常有简单表、分组表和复合表三种。

制表的基本原则是：首先，表的结构要简单明了，一张表只能有一个中心，避免包罗万象的大表。其次，表的层次要清楚，项目排列要按照逻辑顺序合理安排。制表的具体要求是：①标题应简明扼要说明表的内容；②表的内容应分别以横、纵、总报等标题加以说明；③数据书写与精确度要整齐划一；④表中的横竖线条不宜过多。表两端的竖线可以省略。

频数分布表也称次数分布表，常见的有简单频数分布表、累积频数表和累积百分比分布表三种形式。

简单频数分布表编制的步骤如下。

①求全距：R＝A-B，A、B分别为统计数据中最大、最小的数值。

②决定组数与组距。欲将所有数据划分为若干组时，要先确定组数与组距。组数一般以10个左右为宜。组数确定后，组距（i）可以利用下列公式来求。

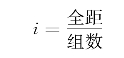
组距一般以3、5、7等奇数个单位为宜。但有时也可以先定组距i，再求组数。

③决定组限。组限就是每组的起止范围，每组的最低值为下限，最高值为上限。

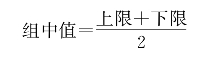
④登记频数。分好组后，就可以将每个数据归入相应的组内，并以符号Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ或“正”字逐个登记，然后求出每组内的总数f。这个总数f就称为频数或次数。

（3）统计图、频数分布图的绘制。统计图是以点、线、面、体来表示各种数据间关系及其变动情况的重要工具，它形象直观，便于整体比较。常见的统计图有条形、圆形、曲线形和象形图几种。制图的基本规则有以下八条。

①根据资料的性质和分析的目的，选择适合的图形。

②图的标题要简明扼要，切合图的内容；标题一般写在图形的下方。

③图的尺度线与图形基线要垂直，尺度分点要清楚，以便于读数与计数。不能用同一尺度表示性质不同的两种计数单位。

④图的横坐标与纵坐标的数字分别按卡尔坐标形式自左向右由小到大或自上而下由大到小分布。

⑤图中线条的粗细应依其重要性而有所区别。

⑥在同一个图例中比较两个事物时，使用的比例要相同，数量大小最好用条形图的长短来表示，其宽度保持一致。

⑦图形中如有必要另加解释的地方，可用图注加以说明。图注应简明扼要，字体偏小并写在图题的下方。

⑧为了美观易看，有横纵轴的图形的宽度与高度之比以接近5∶3为宜。

频数分布图也称次数分布图，是以曲线或折线来表示相应的频数分布表的一种统计图。

直方图是以面积来表示频数的分布，即用位于横轴上各组上下限之间的矩形面积表示各组频数分布的情形。制图方法如下。

①作横轴，然后把各组的上下限或组中值分别标于横轴上，但要在横轴的两端至少各空一个组距的位置。

②作纵轴，在纵抽上标明尺度及单位以指示频数。

③按各组的频数在纵轴上作出与横轴平行的直线。这一直线便与横轴上的上下限组成一个直立矩形。由于横轴上各组距之间是连续的，故所有的矩形组成一个并立的直方图。

多边图是以相应的纵轴上的高度点来表示频数的分布情况的图形。它的制作可以在直方图的基础上进行，所不同的是，它以各组的组中值点为横坐标，以各组的频数为纵坐标描出相应的代表点来，然后用直线段把相邻的两点连接起来，最后形成一条起于或止于横轴的折线。当且仅当起、止点均在横轴上时，这一折线就与横轴构成一个封闭的多边形。

（4）集中量与差异量的计算。所谓集中量，指的是一个群体性的代表数值。它表明了某个群体的数量特征，一般用于对群体间的比较，以分辨一群体与另一群体的差别。用来描述集中趋势的量数，常见的有算术平均数、中位数、众数等。

①算术平均数。算术平均数就是某组数据的总和除以该组数据的总个数所得之商。即

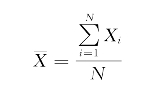
常简写成

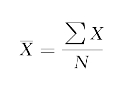
还有一种加权算术平均数，它是将每一数据X与相应的权数W（或者数据出现的次数f）之乘积的加总之后，再除以权数（或次数）之和，即

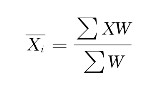
平均数的计算有许多简便方法，可参考一般的统计学教科书。

②中位数：当一组数据按大小顺序排列后，那个居于中间位置的数就是中位数，记为Mdn。当数组的个数为偶数时，中位数就是位于中间那对数的平均数。当靠近中间那个数左右有相同的数时，确定中位数的大小就比较复杂了，这可以参考有关的统计学教科书。

③众数。指的是在一组数据中，出现次数最多的那个数，记为M0。在次数分布表中，众数常以出现次数最多的那一组数的组中值来代替。在次数分布图中，则以曲线上纵坐标最大的那个点相对应的横坐标为众数，可以用公式M0＝3Mdn-2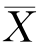来计算。

有关分组后的众数与中位数的计算，可以按下列公式进行

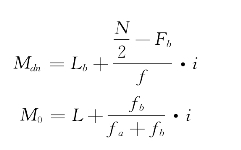
式中：Lb＝中位数所在组的精确下限；

Fb＝中位数所在组精确下限以下的累积次数；

f＝中位数所在组的次数；

i＝组距；

L＝众数所在组的精确下限；

fa＝众数所在组下限相邻一组数的次数；

fb＝众数所在组上限相邻一组数的次数。

有时，两个群体的集中趋势相同，但离中趋势不同。例如，两个人数相同的班级的数学平均分数均为70分，但甲班最高分为95，最低分为45，而乙班最高分为85，最低分为65，这说明这两个班的数学成绩并不是相同的。因此，还要考查分布的离散程度，即要计算出差异量。所谓差异量，指的是描述一组数据变异程度或离散程度的数量。集中量数指的是量尺上的一个点，差异量数指的是量尺上的一段距离，一个分布的差异量数越大，说明集中量数的代表性越小，反之，集中量数的代表性就越大。通常用来描述分布离散性的差异量数有两极差、方差与标准差、变异系数、百分位差、四分位差和平均差等。下面介绍最常用的几种。

①两极差，即全距，记为R，R＝最大数值-最小数值，它反映整个数据资料分布的范围。

②方差与标准差，它们是最常用的差异量，一般与算术平均数相互配合使用。

方差就是某数组中每个数据与其算术平均数的差的平方和除以该组数据总个数之商，以符号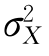表示。

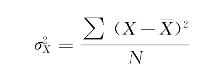
为了使差异量与数据的单位一致，将方差开平方即得到标准差，记为σX，即：

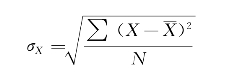
对于分组后的数据资料，计算方差与标准差可利用下列方式

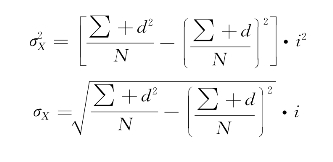(www.zuozong.com)

式中：∑为∑（X-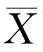）2；

N为数据的总个数；

i为组距。

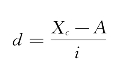
式中：A为假定平均数，但A一般取众数或中位数所在组的组中值；Xc为各个组的组中值。

当数据比较多时，通常是先分组，再利用上述公式求其标准差。但也可以采用下列公式通过小组的标准差来求总体标准差St。

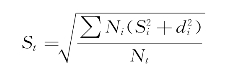
式中：St＝总体标准差；

di＝各组平均数与总平均数之差，即；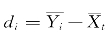

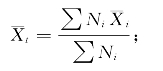
Ni＝第i组数据的总个数（i＝1，2，…，K）；

Nt＝∑Ni（i＝1，2，…K）；

St＝各组的标准差。

③变异系数：变异系数又称差异系数或变差系数，是标准差与平均数的比率，用符号CV表示。即

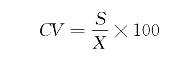
由这个公式不难看出，差异系数是相对差异量，而前面所讲的是绝对差异量。当两组数据单位相同且平均数相差不大时，可以直接用差异量来比较它们的离中趋势的大小。但是，如果比较的对象单位不同或单位相同但平均数相差很大时，用差异量来比较离中趋势就不行了。

例如，某公司年终考评，所得员工销售额与销售量的分数如表4-17所示。

表4-17　员工的销售额与销售量的数据

显然，这里测量数据的单位不同，故不能用标准差来比较两组数据的离散程度。若从标准差来判断，可能会误认为销售额的离散程度大，实际上，从变异系数看，销售量的离散程度比销售额的离散程度要大得多。因此，在这种情况下，应以变异系数来比较。

（5）相关系数计算。若从两组数据相互变化的增减趋势来看，相关系数可分为正相关和负相关；若从表现形式上来看，可分为直线相关与曲线相关；若从两组数据的相互关系上看，可分为完全相关、高度相关和零相关三种。分析相关的方法通常有图示法和计算法两种。计算法是最常用的一种方法，这种方法一般是通过相关系数的计算，从相关系数的大小来揭示相关程度的一种方法。计算相关系数的方法很多，下面介绍积差相关、等级相关和点二列相关三种计算方法。

第一种，积差相关系数的计算。计算积差相关系数的基本公式是：

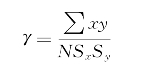
式中：x＝x-；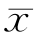

y＝y-；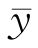

N为成对的相关量数目；

Sx为以x为代表的数组的标准差；

Sy为以y代表的另一数组的标准差。

根据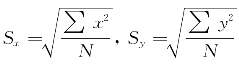，上式又可以变为：

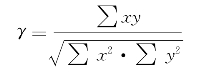
第二种，等级相关系数的计算。有时，主管对员工的评定不是用划分更小单位的百分制分数来记分，而是以优、良、中、可、劣的等级制来记分。计算类似这种顺序变量的相关系数就要用到等级相关系数计算法。这种方法是把两组对象按某种顺序排列，并根据各变量所在等级的位置的差来计算相关系数。它的计算公式为：

式中：γp表示等级相关系数；

D＝Rx-Ry；

Rx，Ry分别表示同一行配对的两个数据的等级数；

N表示等级的个数。

当N＜30，数据为连续变量，又希望采用较简便的方法求相关系数，只要把N个连续变量看成N个等级，便可采用等级相关法。其计算步骤如下。

①将变量x填入计算表的X列，把x变量按大小顺序排成等级（最大的变量为第1等，次大的变量为第2等，以此类推）填入表的Rx列。

②将与x变量相对的y变量填入Y列中，并把y变量的等级数列填入Ry列中。

③分别求出对应等级的差数D及D2列。

④求∑D2。

⑤将上述各数据代入公式求γp。

第三种，点二列相关系数的计算。当一个变量属于连续变量，而另一个变量属于只分两个性质的二分名称变量，如男与女、是与否、对与错、已婚与未婚等。要考查这类二分变量与连续变量之间的相关，就需要计算点二列相关系数了。

计算公式如下：

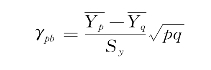
式中：γpb表示点二列相关系数；

p表示二分变量中某项所占的比例；

q表示二分变量中另一项所占的比例，q＝1-p；

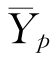表示与p部分相对应的连续变量的平均数；

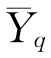表示与q部分相对应的连续变量的平均数；

Sy表示全体连续变量的标准差。

点二列相关系数的计算步骤如下。

①以二分变量为x变量，分别求出二分变量的各项的比例数p及q。

②以连续变量为y变量，分别求出及Sy。

③代入公式求出点二列相关系数γpb。