定量决策法:理性决策的利器

1）确定型决策方法

确定型决策方法，比较常见的是线性规划方法和盈亏平衡分析法。

（1）线性规划方法

线性规划（Linear programming，LP）是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支。它是辅助人们研究线性约束条件下线性目标函数的极值问题、进行科学管理的一种数学理论和方法，实践中被广泛应用于军事作战、经济分析、经营管理和工程技术等方面，为合理地利用有限的人力、物力、财力等资源作出的最优决策，提供科学的依据。线性规划方法主要运用于解决两类问题：

①资源一定的条件下，力求完成更多的任务，取得好效益。

②任务一定的条件下，力求资源节省。

具体掌握线性规划方法，有待于深入地学习“运筹学”这门课程。

（2）盈亏平衡分析法

盈亏平衡分析（Break-even analysis）又称保本点分析或本量利分析法，是根据产品的业务量（产量或销量）、成本、利润之间的相互制约关系的综合分析，用来预测利润，控制成本，判断经营状况的一种数学分析方法。重点是通过盈亏平衡点（BEP）判断项目成本与收益的平衡关系。各种不确定因素（如投资、成本、销售量、产品价格、项目寿命期等）的变化会影响投资方案的经济效果，当这些因素的变化达到某一临界值时，就会影响方案的取舍。盈亏平衡分析的目的就是找出这个临界值，即盈亏平衡点（BEP），判断投资方案对不确定因素变化的承受能力，为决策提供依据。盈亏平衡点的计算方法是：

首先，确定盈亏平衡点产量：

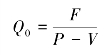
其次，计算盈亏平衡点销售收入：

这里，S＝P·Q，

S——收入，

P——单价，

Q——产量，

C——成本，

其中，

F——固定成本，V——单位变动成本，且C＝F＋V·Q。

2）风险型决策的方法

风险型决策是指每个备选方案都会遇到几种不同的可能情况，而且已知出现每一种情况的可能性有多大（即发生的概率），因此在依据不同概率所拟订的多个决策方案中，不论选择哪一种方案，都要承担一定的风险。常见的风险型决策法主要有期望值决策法、决策树法。

（1）期望值决策法

先介绍与期望值决策法有关的3个重要概念：

①先验概率。它根据过去经验或主观判断而形成的对各自然状态的风险程度的测算值。

②自然状态。它是指各种可行的备选方案可能遇到的客观情况和状态。

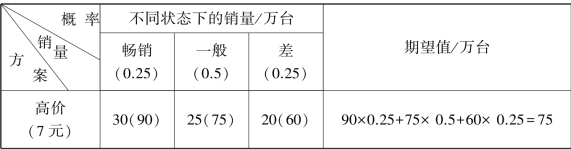
③损益矩阵。它一般由3部分组成：可行方案、自然状态及其发生的概率、各种行动方案的可能结果。把这3部分内容在一个表上表现出来，这个表就是损益矩阵表。（表5.2）

期望值决策法的步骤：计算各方案的期望值，据期望值比较，判断方案的优劣。其计算公式为：期望值E＝效价V×概率P。

举例：不同方案的销路及概率（成本4元／台）

表5.2　损益矩阵例表

续表

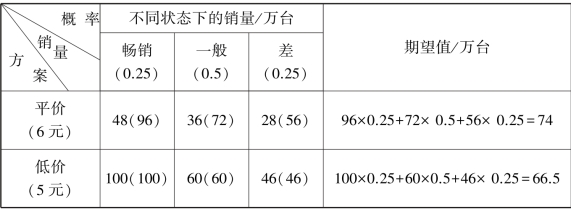
在本例中，显然，根据期望收益值大小，“高价”销售方案是最优方案。

（2）决策树法

决策树法是运用概率与图论中的树对决策中的不同方案进行比较，从而获得最优方案的风险型决策方法。图论中的树是连通且无回路的有向图，入度为0的点称为树根，出度为0的点称为树叶，树叶以外的点称为内点。决策树由树根（决策节点）、其他内点（方案节点、状态节点）、树叶（终点）、树枝（方案枝、概率枝）、概率值、损益值组成。熟练地掌握决策树法，有待于深入学习“运筹学”这门课程。

决策树法是用树状图来描述各种方案在不同自然状态下的收益，据此计算每种方案的期望收益从而作出决策的方法。这种最简单情形下的决策树法本质上与期望值决策法一致。

如图5.4所示，今天能逃课吗？具体的计算过程可以自己完成。

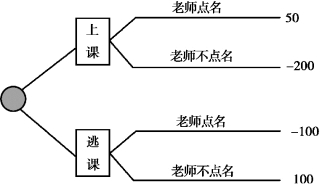
图5.4　逃课／上课的决策树

3）不确定型决策方法

当决策者无法确定各种方案成功的可能性时，决策者知道将面对一些自然状态，并知道将采用的几种行动方案在各个不同的自然状态下所获得的相应收益值。但决策者不能预先估计或计算出各种自然状态出现的概率。这样的决策就是不确定型决策。

不确定型决策需要决策的问题存在较大的风险，故使用的决策方法在很大程度上取决于决策者对风险的态度。不同人的风险价值观差异很大，但大体上分为3类：保守型、进取型、稳妥型。依据这3种风险价值观，不确定型决策的管理者可采用的决策方法可以分为4类：

（1）乐观决策法

乐观决策法又称“大中取大法”，即找出每个方案在各种自然状态下的最大损益值，取其中最大者，所对应的方案即为合理方案。很显然，这一做法是比较冒险的，通常被一些冒进主义者所采用。

（2）悲观决策法

悲观决策法又称“小中取大法”，即找出每个方案在各种自然状态下最小损益值，取其中最大者，所对应的方案即为合理方案。这一做法显然是比较保守的，通常被一些悲观主义者所采用。

（3）最小后悔值法

最小后悔值法又称“大中取小法”，其计算原理是：首先，将每种自然状态的最高值（是指收益矩阵，若是损失矩阵应取最低值）定为该指标的理想目标；其次，将该状态中的其他值与最高值相减所得之差称为未达到理想的后悔值，并把后悔值排列成矩阵称为后悔矩阵，它可以从收益矩阵中导出来；再次，把每个行动方案的最大后悔值求出来；最后，再求出所有最大后悔值中最小的一个，所对应的方案作为决策方案。

（4）等概率法

还有一种情形就是，不确定型决策是事先无法估计出每种自然状态所出现的概率，但最简单的情形就是依据等可能性准则，假定每一种自然状态出现的概率相等，这样就将不确定型决策问题转换为风险型决策问题，可以运用期望值决策法加以决策。

等可能性准则的想法是这样的：决策人在决策过程中，不能肯定哪种状态容易或不容易出现时，便认为它们出现的可能性（概率）是相等的。如果有n个自然状态，那么可以认为每个自然状态出现的概率相等，都是1／n；然后利用风险型的决策办法，求出各策略的收益期望值，并根据收益期望值的大小进行决策，这个决策准则是法国数学家拉普拉斯（Laplace）首先提出的，所以又叫拉普拉斯准则。(www.zuozong.com)

例如：假设有A1至A5 5种备选方案，存在B1至B4 4种无法把握的自然状态，矩阵中的数据分别为各备选方案在各种自然状态下的损益值。分别应用乐观决策法、悲观决策法、最小后悔值法和等概率法进行决策。

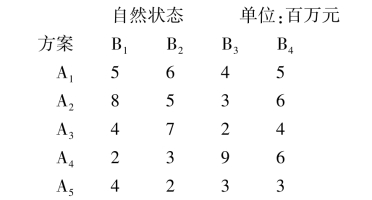
①基于乐观准则的决策过程：

首先，把各个方案在各种自然状态的最大收益值求出来。

a1：max｛5，6，4，5｝＝6

a2：max｛8，5，3，6｝＝8

a3：max｛4，7，2，4｝＝7

a4：max｛2，3，9，6｝＝9

a5：max｛4，2，3，3｝＝4

在矩阵中表示如下：

其次，求各最大收益值中的最大值。

max｛6，8，7，9，4｝＝9

最后，最大收益值9所对应的方案A4即为乐观决策法下的最优方案。

②基于悲观准则的决策过程：

首先，把各个方案在各种自然状态的最小收益值求出来。

a1：min｛5，6，4，5｝＝4

a2：min｛8，5，3，6｝＝3

a3：min｛4，7，2，4｝＝2

a4：min｛2，3，9，6｝＝2

a5：min｛4，2，3，3｝＝2

在矩阵中表示如下：

其次，求各最小收益值中的最大值。

max｛4，3，2，2，2｝＝4

最后，最大收益值4所对应的方案A1即为悲观决策法下的最优方案。

③基于“后悔值”决策准则的决策过程：

首先，把各种自然状态在各个方案下的最大收益值找出来。

b1：max｛5，8，4，2，4｝＝8

b2：max｛6，5，7，3，2｝＝7

b3：max｛4，3，2，9，3｝＝9

b4：max｛5，6，4，6，3｝＝6

在矩阵中表示如下：

其次，将该状态中的最高值减去其他值，所得之差为未达到理想的后悔值，然后把后悔值排列成矩阵，称为后悔值矩阵，如下所示：

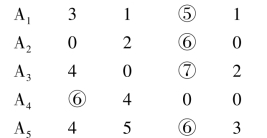
再次，在后悔值矩阵中找出每个行动方案的最大后悔值。

a1：max｛3，1，5，1｝＝5

a2：max｛0，2，6，0｝＝6

a3：max｛4，0，7，2｝＝7

a4：max｛6，4，0，0｝＝6

a5：max｛4，5，6，3｝＝6

最后，再找出所有最大后悔值中最小的一个。

min｛5，6，7，6，6｝＝5

最小的后悔值5所对应的方案A1，即为利用最小后悔值法得出的最优方案。

④基于等可能性准则的决策过程：

首先，假定B1至B4的4种自然状态出现的概率相等，即p1＝p2＝p3＝p4＝0.25。

其次，计算每种备选方案的期望收益值E，如下所示。

最后，期望收益最大值为5.5，所对应的方案A2即为等概率法决策的最优方案。