稳态时的经济增长率与内生变量研究

下面考虑当经济达到稳态时，新古典增长模型中的相关内生变量的增长率。分没有技术进步的新古典增长模型和具有技术进步的新古典增长模型两种情况来说明。先考虑前者。根据图7-5，可知经济的稳态出现在D点，对应于D点，求得人均资本k、人均产量Y和人均储蓄（投资）的稳态值分别为k*、y*和sy*，由于k*和y*都为常数，故可知它们的增长率均为零，即：

该方程说明了新古典增长模型中的一个非常重要的结论，即人均资本和人均产出的稳态增长率均为零。出于这个原因，可以说在没有技术进步的情况下，新古典增长模型并没有对长期人均增长的决定因素作出解释。

进一步地，由于k＝和y＝，同时注意到人口增长率为n，

即有：

上式说明，在不考虑技术进步的情况下，总量资本和总产出的稳态增长率为n，即人口增长率。上述结论如表7-1所示。

表7-1　没有技术进步的新古典增长模型的稳态增长率

(www.zuozong.com)

续表

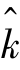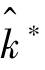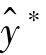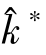现在说明具有技术进步的新古典增长模型的稳态增长率。根据该模型的稳态条件方程式可知，在f（）给定及参数S、n、a和δ确定的情况下，该方程能决定一个确定的，将其代入生产函数即可求得，而这里的和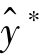又都是不依赖于时间的常数，故它们的增长率均为零。

又由于在具有技术进步的新古典增长模型中，和的定义如下：

再结合关于增长率的相关理论和结论，并注意到人口增长率为n和技术进步增长率为a，便形成如表7-2所示的结果。

表7-2　具有技术进步的新古典增长模型的稳态增长率

根据表7-2可知，在加入技术进步因素后，新古典增长模型终于可以解释本章前面所展示的生活水平的持续提高。也就是说，技术进步会导致人均产出的持续增长。一旦经济达到稳态，人均产出的增长率就只取决于技术进步的速率。根据新古典增长模型，只有技术进步才能解释持续增长和生活水平的持续上升。