圆锥曲线问题在江苏高考中的应用

望亭中学　曹黎星

【摘要】　圆锥曲线方程是解析几何的主要内容，包括椭圆、双曲线、抛物线三种圆锥曲线。圆锥曲线试题是每年高考题的必备题型，很受试卷命题人的青睐。江苏高考中的圆锥曲线问题全面体现了新课程标准的要求，既关注了对学生数学基础知识、基本技能、基本思想方法的考查，更注重了对学生处理数学综合问题能力的考查。

【关键词】　高考；圆锥曲线；解析几何

圆锥曲线方程是解析几何的主要内容，包括椭圆、双曲线、抛物线三种圆锥曲线。圆锥曲线试题是每年高考题的必备题型，很受试卷命题人的青睐。圆锥曲线试题是高考成绩的分水岭，许多中等成绩的同学在处理此类题目时，往往难以下手，不知如何处理繁杂的条件。为了使同学们有效地分析并把握江苏高考中圆锥曲线题命题的趋势，笔者认真剖析了高考考试大纲中圆锥曲线的有关重点、热点，对2004年至2013年这十年中江苏高考试题中圆锥曲线题进行了初步统计及分析，以便于同学们有针对性地进行复习备考。

一、利用圆锥曲线定义

【案例1】　（江苏2005年，5分）若抛物线y＝4x2上的一点M到焦点的距离为1，则点M 的纵坐标是_________。

【考点】抛物线的定义。

【分析】根据点M到焦点的距离为1，利用抛物线的定义可推断出M到准线的距离也为1，利用抛物线的方程求得准线方程，从而可求得M的纵坐标。根据抛物线的定义可知M到焦点的距离为1，则其到准线的距离也为1。又因为抛物线的准线为y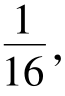＝－，所以点M的纵坐标为

【案例2】　（江苏2007年，5分）在平面直角坐标系xOy中，已知△ABC顶点A（－4，0）和C（4，0），顶点B在椭圆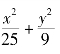＝1上，则＝___________。

【考点】椭圆的定义，正弦定理。

【分析】利用椭圆定义和正弦定理得a＋c＝2×5＝10，b＝2×4＝8，

所以

【例3】　（江苏2010年，5分）在平面直角坐标系xOy中，双曲线上一点M，点M的横坐标是3，则M 到双曲线右焦点的距离是__________。

【考点】双曲线的定义。

【分析】设d为点M到右准线x＝1的距离，MF为M到双曲线右焦点的距离。根据双曲线的定义，得，而d＝2，所以MF＝4。

二、应用圆锥曲线性质确定离心率

主要利用圆锥曲线的基本性质来求解离心率。

【例4】　（江苏2004年，5分）若双曲线的一条准线与抛物线y2＝8x的准线重合，则双曲线的离心率是_________。

【考点】双曲线的性质，抛物线的性质。

【分析】根据抛物线方程可求得抛物线的准线方程即双曲线的准线方程，从而求得c，最后根据离心率公式求得答案：由抛物线y2＝8x，可知p＝4，所以准线方程为x＝－2。双曲线的准线方程为x＝－＝－2，所以2c＝a2＝8，c＝4。所以双曲线的离心率e＝＝

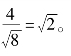
【例5】　（江苏2009年，5分）如图1，在平面直角坐标系xOy中，A1，A2，B1，B2分别为椭圆的四个顶点，F为其右焦点，直线A1 B2与直线B1 F相交于点T，线段OT与椭圆的交点M恰为线段OT的中点，则该椭圆的离心率为_________。

【考点】椭圆的基本性质。

【分析】∵A1，A2，B1，B2为椭圆（a＞b＞0）的四个顶点，F为其右焦点，∴直线A1 B2的方程为直线B1 F的方程为二者联立解得又∵点M恰为线段OT的中点，∴又∵点M在椭圆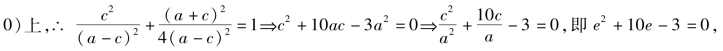解得

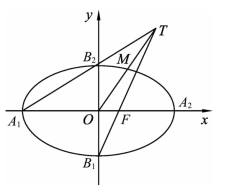
图1

三、圆锥曲线综合问题中的定点和定值问题

【例6】　（江苏2010年，16分）如图，在平面直角坐标系xOy中，已知椭圆的左、右顶点为A，B，右焦点为F。设过点T（t，m）的直线TA，TB与椭圆分别交于点M（x1，y1），N（x2，y2），其中m＞0，y1＞0，y2＜0。

（1）设动点P满足PF2－PB2＝4，求点P的轨迹；

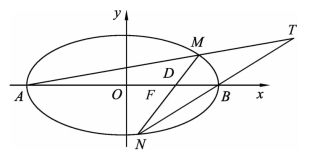
图2

（2）设求点T的坐标；

（3）设t＝9，求证：直线MN必过x轴上的一定点（其坐标与m无关）。

略解：（1）点P的轨迹为直线x＝。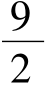

（2）点T的坐标为

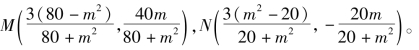（3）∵点T的坐标为（9，m），∴直线TA的方程为即直线NT的方程为即分别与椭圆方程联立，同时考虑到x1≠－3，x2≠3，求得当x1≠x2时，直线MN的方程为

令y＝0，解得x＝1。此时必过点D（1，0）；当x1＝x2时，直线MN方程为x＝1，与x轴的交点为D（1，0）。

所以直线MN必过x轴上的一定点D（1，0）。

【考点】轨迹方程，直线与圆锥曲线的综合问题。

【分析】第（3）问中求出直线方程的参数表达式，然后求出其与x轴的交点的坐标，得到其横坐标为一个常数，从而说明直线过x轴上的定点。

(www.zuozong.com)

图3

还可以这样证明：根据特殊情况即直线与x轴垂直时的情况求出定点，然后证明不垂直于x轴时两线DM与DN斜率相等，说明直线MN过该定点。

【例7】　（江苏2012年，16分）如图3，在平面直角坐标系xOy中，椭圆的左、右焦点分别为F1（－c，0），F2（c，0）。已知（1，e）和都在椭圆上，其中e为椭圆的离心率。

（1）求椭圆的方程；

（2）设A，B是椭圆上位于x轴上方的两点，且直线AF1与直线BF2平行，AF2与BF1交于点P。

①若AF1－BF2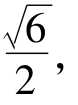＝求直线AF1的斜率；

②求证：PF1＋PF2是定值。

解：（1）椭圆的方程为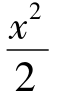＋y2＝1。

（2）①直线AF1的斜率为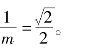

②证明：∵AF1∥BF2，∴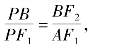

即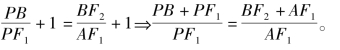

∴

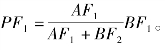
由点B在椭圆上知

∴

同理

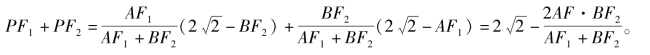
其中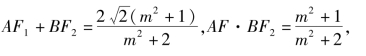

∴

∴PF1＋PF2是定值。

【考点】椭圆的性质，直线方程，两点间的距离公式。

【解析】（1）根据椭圆的性质和已知（1，e）和都在椭圆上列式求解。

（2）根据已知条件用待定系数法求解。

四、圆锥曲线中的分类讨论思想

根据点的位置的不同进行分类讨论。

【例8】　（江苏2004年，12分）已知椭圆的中心在原点，离心率为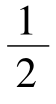，一个焦点是F（－m，0）（m是大于0的常数）。

（1）求椭圆的方程；

（2）设Q是椭圆上的一点，且过点F，Q的直线l与y轴交于点M，若求直线l的斜率。

解：（1）所求的椭圆方程是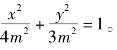

（2）设Q（xQ，yQ），直线l：y＝k（x＋m），则点M（0，km）。

当＝2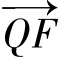时，由于F（－m，0），M（0，km），由定比分点坐标公式，得

又因为点在椭圆上，所以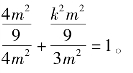

解得

当

于是，解得k＝0。

故直线l的斜率是0，±2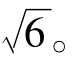

【考点】椭圆的标准方程，直线l的斜率。

【分析】（1）由椭圆的中心在原点，离心率为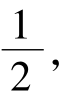，一个焦点是F（－m，0），可用待定系数法求出椭圆的方程。

（2）分两种情况由定比分点坐标公式求解即可。

总之，江苏高考中的圆锥曲线问题全面体现了新课程标准的要求，既关注了对学生数学基础知识、基本技能、基本思想方法的考查，更注重了对学生处理数学综合问题能力的考查。

（本文发表于《高中数学教与学》〈教研版〉2014年第2期）