高效遗传算子的优化方法是什么

本节介绍前面提出的带模糊逻辑控制器的遗传算法中的高效遗传算子，包括交叉算子、选择算子和变异算子。

1.权重重置交叉算子

遗传算法中交叉的作用是寻找新的解空间，交叉算子是对被选定的父母染色体交换其部分基因字符串。由于基于优先级的编码输入排列编码，故算法中可以使用基于排列编码的交叉算子，如部分重置交叉算子（PMX）、顺序交叉算子（OX）和定位交叉算子（PX）等。

部分重置交叉算子（PMX）和顺序交叉算子（OX），分别由Goldberg和Lingle（1995）以及Davis（1995）提出，可以视作传统的两切点交叉算子的变形[236，237]，而由Syswerda 提出的定位交叉算子则为均匀交叉算子的变形[238]。针对解决可能不合法或不合格的子女群体的产生，这些交叉算子有特定的修复程序。在带模糊逻辑控制器的遗传算法中使用权重重置交叉算子，是Gen[239]提出的，参见图5.4。Gen 将以上提到的四种交叉算子分别应用到遗传算法中，并对其相对应的算法性能进行了研究[239]。权重重置交叉算子可以看成关于排列编码的单切点交叉算子的扩展变形。作为单切点交叉算子，在权重重置交叉算子中，随机选取一个切点后，其子女代是由两部分产生构成的，即由切点左边的部分和重置父母代切点右边的部分构成。事实上，这类重置操作等同于对父母代的随机变形。图5.4给出了权重重置交叉算子的一个例子。在图5.4中，随机选取的切点为8，切入点之后右边部分的权重分别为：1→2，3→4，5→6 和6→7。使用这些权重对第二个父母进行重置，可获得第一个子女产生的新的右边部分为4，2，6 和7。同样地，对第一个父母进行同样设置，以获取第二个子女的染色体序列。

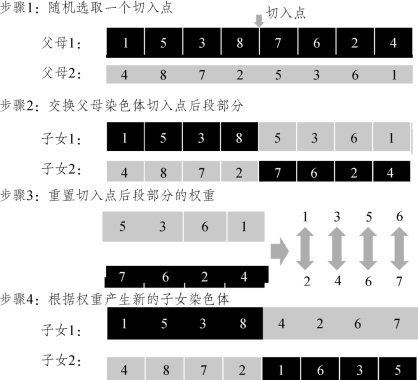
图5.4　权重重置交叉算子

2.互换变异算子

变异的作用与交叉的作用类似。交叉是为了防止算法过早收敛，同样也是为了探索新的解空间。与交叉不同的是，变异并没有涉及两条染色体，一般是对一条染色体上的基因进行改进。Gen 同样研究了两种变异算子，即插入变异算子和互换变异算子，分别探讨这两种算子对遗传算法性能的影响[239]。其中，插入变异算子指的是随机选取染色体上的一个数字，随后将该数字随机插入该染色体的一个新位置上。互换变异算子为在一条染色体上随机选取两个基因（数字），随后将这两个基因在染色体上的位置互换。图5.5分别给出了插入变异算子和互换变异算子的例子。此处，在带模糊逻辑控制器的遗传算法中使用互换变异算子。(www.zuozong.com)

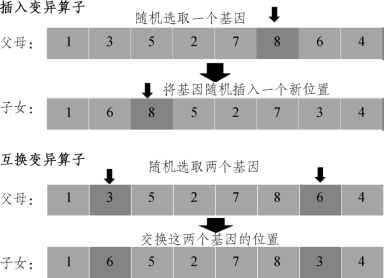
图5.5　互换变异算子

3.轮盘赌选择算子

选择之前，先要对染色体的优劣进行评估。评估是计算每个染色体的适应函数值，通过适应函数值反映个体染色体的拟合优度。评估的过程是将单个染色体和种群中其他染色体进行比较。这里，适应函数的选取十分关键，因为它直接涉及染色体改进提高的趋势和方向。使用适应函数对每一代所产生的解进行评估，故而对适应函数值的计算效率的要求必须很高。即分别选取上跟随者的目标函数并作为上跟随者染色体更新的适应函数。

算法中的遗传操作（交叉和变异）可视为探索新的解空间的勘探过程，而选择操作则作为指引算法进化方向的开发过程。这里选取轮盘赌选择算子作为选择机制。轮盘赌选择算子是一种成比例选择机制，基本思路为：选定每一条染色体的选择率或存活率并使之与其适应函数值成正比，随后建立展示所有染色体的概率的轮盘赌模式。选择过程为每次转动轮盘后选择其中一条染色体作为新一代染色体，其中转动轮盘的次数与种群大小相同。轮盘的特点使得选择过程为随机抽样过程。图5.6给出了一个轮盘赌选择算子的实例。从图5.6中可以看出，轮盘上显示了所有染色体的概率，其中最合适或者适应函数值最好的染色体占有最大份额，最弱或者适应函数值最差的染色体占有最小份额。随着轮盘的旋转，选取点会选择其中一条染色体作为新的一代，并且最合适的染色体被选上的概率是最高的。

图5.6　轮盘赌选择算子