参数处理：基于期望值算子的模糊随机变量优化方法

实际上，不确定是绝对的，而确定是相对的，现在，模糊随机变量已经被应用到很多领域，如仓储问题[222]、项目进度问题[116]、报酬更新过程问题[38]以及供应链问题[223]。这些研究已经证明，模糊随机理论在处理随机信息和模糊信息共存的问题上具有一定的有效性。

然而，处理不确定变量，尤其是模糊随机变量，是十分困难的。针对模糊随机变量，Kwakernaak 给出了其数学表达式[93，184]，随后 Puri 和Ralescu 将此数学形式定义得更加清晰[97]。在Kwakernaak 或Puri 和Ralescu的理论中，模糊随机变量被看作一组典型的取实值的随机变量的“模糊感知、观察或者印象”。由于不能够直接获取或者计算出模糊随机变量的数值，故提出一个用期望值算子对包含模糊随机变量的目标函数进行处理。根据可测集值函数的Aumann 积分，Puri 和Ralescu 将模糊随机变量的期望值定义为模糊数[97]。

【定义4.1】[97] 给定概率空间（Ω，F，P），如果对 ∀ω ∈ Ω，α ∈[0，1]，映射ω ↦ξα-（ω）和ω ↦ξα+（ω）是可积的，则称ξ 为关于概率空间（Ω，F，P）的积分有界的模糊变量。

【定义4.2】[97] 设ξ 是概率空间（Ω，F，P）上积分有界的模糊随机变量，ξ 的期望值 E （ξ）被定义为R 上唯一的模糊集，对∀α ∈（0，1]，满足：

其中是 ξα 关于P 的Aumann 积分，L1 （P）表示关于概率测度P 可积的全部函数 f：Ω→R。

设（Ω，F，P）为完备概率空间，ξ：Ω→FC （R）为积分有界的模糊随机变量[107]，则对∀α ∈（0，1]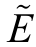， （ξ）的 α-截集可以表示为如下的紧凸区间：

设（Ω，F，P）为完备概率空间，ξ1，ξ2为定义在（Ω，F，P）上积分有界的模糊随机变量，λ，γ ∈ R，则有[107]：

【定义4.3】[186] 设ξ 是定义在概率空间（Ω，F，P）上的一个模糊随机 变量，它的期望值定义为：

在等式（4.4）两边同时出现符号E，然而这两个E 代表不同的含义，其中一个为模糊随机变量的期望值算子，另一个为模糊变量的期望值算子。

当模糊随机变量ξ 退化为随机变量时，（4.4）式可改写为：

它变成了随机变量的期望值。

当模糊随机变量ξ 退化为模糊变量时，（4.4）式可改写为：

它变成了模糊随机变量的期望值[186]。

设ξ 和η 是期望值有限的模糊随机变量，则对于任意常数a，b，有

【定义4.4】[186] 设ξ 是期望值有限的模糊随机变量，则ξ 的方差定义为

有关不同方差的定义和性质可参见文献[88，224~226]。

从Puri 和Ralescu 所给出的定义可以看出，模糊随机变量是从一个可能性空间到一批次的模糊变量的可测函数。粗略地说，模糊随机变量是一个带有随机值的模糊变量。根据文献[222]，可以将模糊随机变量转变为一个模糊区间，由此，该模糊区间可以用一个模糊数来表示。但是，处理含有模糊变量的目标函数仍然比较困难，无法直接获取确定的最优值。为了尽可能地减少信息的缺失，使用Heilpern 提出的期望值理论，将不确定模型转化为清晰等价模型[227]。综上，根据模糊随机理论，提出了一种将模糊随机变量转变为清晰等价变量的转化方法。下面以典型的模糊随机变量，其中为例，介绍此转化方法的一般步骤。

Step 1.将客户所能忍受的最早服务时间，考虑为模糊随机变量。通过历史统计数据及由经验获取的数据，估计模糊随机变量几个参数[m]L，[m]R，μ0和σ02。

Step 2.模糊随机变量的内部参数由群决策方式获得，其取值受决策者保守程度的影响。根据 Puri 和 Ralescu 所给出的定义[97]，将模糊随机变量表示为，其中ρ （ω）~N（μ0，σ02）的概率密度分布函数为 φρ（x），其数学表达式为。假设σ，σ∈[0，supφρ（x）]，是概率水平，r 是可能性水平且r ∈[rl，1]，其中，则σ 和r 均体现决策者的保守程度。(www.zuozong.com)

Step 3.设定 ρσ 为随机变量 ρ （ω）的 σ-cut。

Xu 和 Liu 在他们的文章中提出了一个可以将模糊随机变量转化为类似于梯形模糊数的模糊变量。文献[222]中的研究调整了这个定理及其证明，使其能够更加适用于离散随机变量，而且有着具有模糊性质的浮动上边界、中值、下边界参数。

【定理4.1】[222] 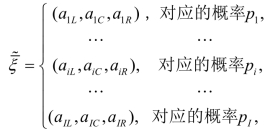是模糊随机变量，有着离散随机分布，在上边界、中值、下边界参数上具有模糊性质的浮动，其中，离散随机分布为 Pψ （x）。设δ 是任意给定的一个随机变量的概率水平，η 是任意给定的一个模糊变量的可能性水平，那么模糊随机变量可以转化为（δ，η）水平梯形模糊变量。

根据Xu 和Liu[222]所给出的引理，，其中ρσ L和ρσ R的取值可以如下表示：

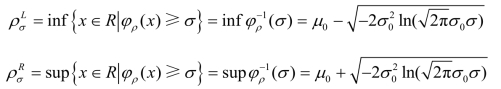
Step 4.将模糊随机变量转化为（r，σ）-level梯形模糊变量，转化公式如下：

其中，

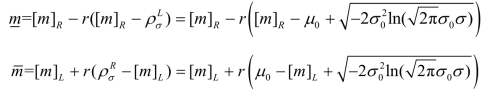
进而，可由表示，其隶属度函数为：

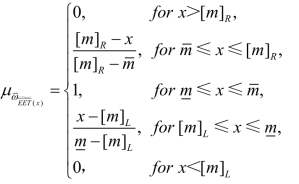
将模糊随机变量转化为（r，σ）-level梯形模糊数的过程参见图4.2。

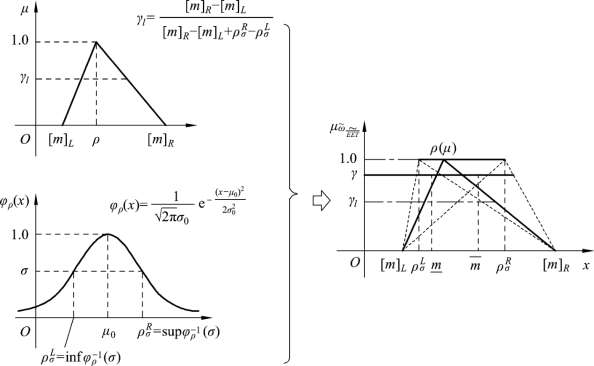
图4.2　模糊随机变量转化过程

Step 5.期望值算子可以将（r，σ）-level梯形模糊变量转变为其清晰等价形式。根据 Heilpern[227]的模糊区间理论和期望值理论，假定一个模糊数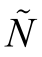=（a，b，c，d），其隶属度函数如下：

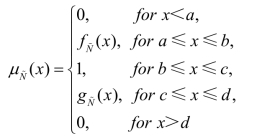
其中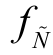（x）和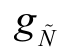 （x）分别是模糊数的上限和下限，此时，模糊数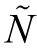的期望值定义为式（4.7）[227]：

所以，模糊变量的期望值如下：

根据以上讨论，可以获得模糊随机时间窗口，如图4.3所示。同样的转换过程可以应用到模糊随机程成本和上。

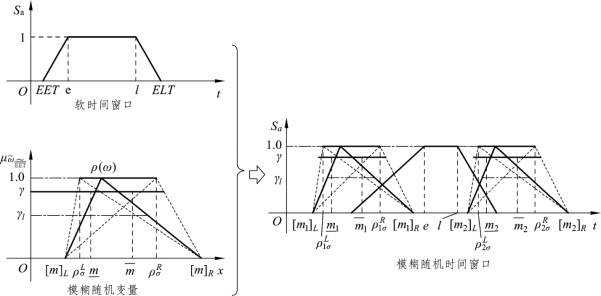
图4.3　模糊随机时间窗口

综上，对模糊随机时间窗口的处理过程可参见图4.4。

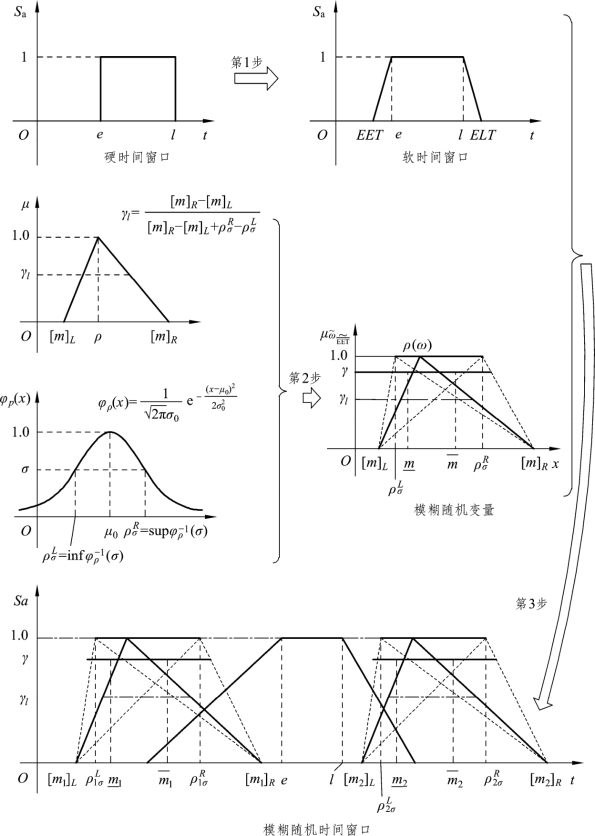
图4.4　模糊随机时间窗口处理过程