构建地理距离空间权重矩阵

各个经济区域之间所拥有的资源是不同的，生产要素的分布也不可能完全均衡，由此必然会导致地区因素极大地影响到区域经济发展[107]。空间数据最显著的特征就是空间的依赖性以及自相关性，较之于传统的计量模型而言，空间计量模型对于较为复杂的区域经济问题具有较强的处理能力。

通过以下三种方式可以用以选择空间权重矩阵：①构建邻接矩阵；②构建基于地理距离的空间权重矩阵；③构建基于经济距离的空间权重矩阵。本书所使用的矩阵模型为第二种，在确定地理距离空间权重矩阵时所依据的是两地间距离的倒数，其权重随着距离的减少而增大，两者的关系为负相关，反之，权重也就越小。定义如下：

这里dij指的是i和j两个不同的资源型城市彼此的间距，具体的计算方式为平均后的铁路和公路距离。(www.zuozong.com)

在实证分析的时候，要明确采取空间计量分析的适用性，因此必须要对其是否具有空间关联性进行检验。如果这种关联性切实存在，那么在实证分析的时候就适合选择空间计量工具。为了验证本书所选取的研究对象是否存在空间相关性，本书借选取的Moran's I指数的公式如下所示：

其中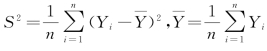，，Yi代表第i个地区的观察值，n为地区总数，Wij为空间权重矩阵。Moran's I应当在[－1，1]的区间内取值，如果Moran's I的取值为0，那么说明各地区空间的相关性表现为正，越是较大的数据，说明越是具有较强的正相关性；小于0表明空间负相关；取值为0则说明各地区间不存在任何的关联性。通过以上公式不难发现，在指数存在非常强的显著性时，其绝对值如果比较接近1，那么就意味着空间的相关性就相对更强。