基于熵权的改进TOPSIS方法

美国数学家香农（1948）最早提出了信息熵的概念[79]，目的是为了对信息进行更好的定量分析。在物理学中，熵是热力学中一个衡量分析混乱程度的概念，香农结合了热力熵的概念，对信息来源的不确定性，提出用信息熵来解释和有效衡量的观点。香农定义的信息熵如下：

假设存在一个离散的随机变量，我们称为：X1＝{x1，x2，x3…，xn}，其信息源以pi＝P（xi）（i＝1，2，…，n）的概率出现，同时，。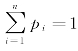

X的信息熵可表示为以下公式[80]。

信息熵的原理是对信息量进行衡量，计算指标的信息熵可以将指标的原始信息体现出来。一般而言，一个指标能够带给我们多少信息量在很大程度上受到了信息熵的影响，信息熵越小，该指标越能够带给我们越多的信息量，其越有贡献于评价结果，所以在综合评价结果中该指标占据着较大的比重。反之，越大的信息熵，意味着越少的信息量，越是较小贡献于综合评价结果，其在综合评价结果中越是占据较少的比重。熵值法作为赋权法的一种相对比较客观。对比因子分析方法，信息熵的过程计算简单，并且限制因素少，比如不需要强调数据的正态分布，等等。

TOPSIS计算模型最早由C.L.Hwang和 K.Yoon（1981）提出，是著名的经典指标计算方法之一[81]。TOPSIS定义了理想值和负理想值。理想值就是最终所形成的方案属于最优，这意味着该方案当中的各项指标都比较好，反之如果这些指标的数据比较低，那么就属于负理想值。通过对比分析，越是靠近理想值的方案，且远离于负理想值，那么在所有的备选方案当中此方案就属于最佳。TOPSIS依据上述方法来找出最优方案。该方法的基本前提是所有变量是递减或者递增，在这个前提下，TOPSIS采用欧式距离的测量方法来对理想值和负理想值进行计算，然后按照优劣的等级来排列各指标最佳解和最差解的欧式距离[82]。离最佳解距离近，离最差解距离远，评估结果好，反之，评估结果差[83]。

1）构建评价矩阵

假设一共有n个待评价的对象，m个评价指标，可以形成原始的数据矩阵R＝（ri，j）m×n：

2）指标的标准化

为了使不同资源型城市绿色转型的各个指标具备一定的可比性，需要对指标的原始数据进行数据标准化处理。一般指标分为效益型指标和成本型指标，效益型指标的数值越大越好，指标的数据标准化公式如下：

消耗性指标：

收益性指标：

根据以上公式对指标原始数据进行标准化处理，得到，且。

3）计算资源型城市绿色转型指标的熵

本研究一共选取了25个指标作为评估指标，选取了101个资源型城市作为研究对象，我们把25个指标定义为m，101个城市作为评估对象，定义为n。具体公式如下：(www.zuozong.com)

4）计算评价指标的熵权

在有m个评估指标、n个评价对象的评估问题中，第i个评价指标的熵权定义式如：

5）构造加权的标准化决策矩阵

即得到加权的标准化决策矩阵

6）确定理想值和负理想值，参见如下公式：

其中，对于效益型指标来说，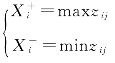

对于成本型指标来说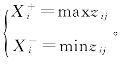

7）欧式距离计算

计算各资源型城市各个指标的值，并计算其与理想值和负理想值的欧式距离和，如以下公式所示：

8）计算相对贴近度

计算各评价对象与理想值的相对贴近度Dj，如下式：

Dj为各评价对象的综合评价得分，Dj越大，评价对象的排名越靠前，转型效果越好；Dj越小，评价对象的排名越靠后，其转型效果越差。