为什么需要方差分析及方差分析的条件

方差分析是F分布最重要的用途之一。方差分析比较复杂，常常需要使用专门的电脑统计软件（如SPSS）。这里，我们只简要讨论一下方差分析的基本原理并举例说明最简单的方差分析的方法和应用。

一、为什么需要方差分析？

简单来讲，方差分析是t检验的一种特殊情况，f检验仅适用于检验两个样本平均数之间的差异是否显著。但是，在语言研究中，我们有时需要同时检验两个以上的样本平均数的差异，比如某次大规模考试中来自几个不同院校的考生的平均成绩是否有显著差异。这时，虽然我们仍可用t检验，但是会带来一定的问题。一是计算量大，费时费力。假如我们有n个样本或n组数据，就有w（w-1）/2对，因而就要进行次r检验。二是当我们做许多t检验时，犯a型错误的概率就会增大。换句话说，差异的显著性会被夸大，这样一来，在总体平均数并不存在差异的情况下，检验却可能会有意义。比如，如果有5组数据，就要做10次f检验；在所有总体平均数都相等的情况下，10个显著水平中至少有一个小于0.05的可能性为29%。而方差分析就可以克服这些问题。运用方差分析，就可以把几个样本平均数同时加以比较，看看它们有没有显著差异。因而方差分析是语言研究中非常常用、非常重要的一个统计分析手段。

二、方差分析的条件

方差分析是一个参数检验，必须满足下列条件：

（一）样本为独立样本；

（二）总体分布为正态；

（三）总体方差相等。

其中，第三个条件可以放松一些，因为即使总体方差之间有些差异，如果各组的样本容量大体相同，也不会对方差分析的结果造成大的影响，因为在这种条件下，方差分析对方差同质性的偏离不是很敏感。但是，如果样本容量差别很大，而总体方差又不相同，就要谨慎了。

三、单因素方差分析与多因素方差分析

方差分析分单因素方差分析与多因素方差分析。所谓“因素”，简言之，就是实验研究所涉及的自变量。比如，我们要研究不同的教学方法对学习成绩的影响，所涉及的自变量就是“教学方法”；再比如，要研究语言难度与内容熟悉程度对阅读理解的影响，就要涉及“语言难度”和“内容熟悉程度”这两个自变量。从另一个角度看，“因素”也可以称为“分组变量”，因为我们以该变量为标准把因变量（我们所收集的数据）分成若干组。例如，在第一个例子中，如果我们的研究涉及三种不同的教学方法，就可以把被试的成绩（因变量）分成三个组；在第二个例子中，如果把阅读材料按“语言难度”分为“难”“较难”“中”“较易”“易”五个等级，就可以把阅读理解成绩（因变量）相应地分成五个组。因此，所谓“单因素方差分析”，就是仅涉及一个自变量或分组变量的方差分析；如果涉及两个以上的自变量或分组变量，则方差分析就为“多因素方差分析”。多因素方差分析不仅计算过程复杂，计算结果的解释也相应地复杂一些。如果用手工计算（也要用具有统计功能的计算器），一般只能处理数据量不是很大的双因素方差分析。就是一些专门的计算机统计软件（如SPSS），能够处理的方差分析的复杂程度也是有限的。当然，由于实验设计、实验实施等方面的种种限制以及实验结果解释的困难，一般的实验只涉及两个或三个自变量。因此，本书仅讨论单因素方差分析和最简单的多因素方差分析——双因素方差分析（但各种规模的方差分析的基本原理都是一样的）。

四、方差分析的基本原理

方差分析是利用F分布来决定几个平均数之间是否有显著差异。方差代表着数据的变异或离散情况。对于一组数据，该变异是由各个观测值之间的差异造成的。如果我们的数据是由几组数据组成的，那么数据的总变异就来自两个方面或是由两个变异源造成的：一是各组内部的差异——由抽样所带来的观测值之间的差异，我们称之为“组内变异”；二是各组平均数之间的差异，称为“组间变异”。

现在，我们假设各组的观测值均来自同一个总体，或来自平均数及方差均相等的总体，这时，数据的总变异就可以看作仅由一个变异源造成的——由抽样带来的变异。如果我们根据组内和组间这两个变异来源，分别计算出总体的方差估计值，那么代表组内变异与组间变异的方差估计值就会大体相等，因而其比值就会大约等于1。但是如果各组观测值来自平均数不同的总体，那么就会有上述两个变异来源，而且组间变异就会远远大于组内变异，两者之比也就会大于1。如果组内变异很小（极端的情况是变异为0，即各观测值都与组平均数相等），而组间变异很大，各组的平均数就有可能是不相同的。

那么，到底组间变异大于组内变异多少时，我们才能说各组平均数之间的差异显著呢？这就要利用F分布进行f检验。(www.zuozong.com)

五、单因素方差分析

（一）总变异的分解

从以上分析可以看出，方差分析的关键是把数据的总变异分解为两个部分：反映各组内观测值离散程度的组内变异和反映各组平均值之间差异大小的组间变异。因此，我们先来看看如何分解总变异。

我们在分解总变异时，被分解的实质上是（×-×）2这一部分，即离均差的平方和。

为了讨论方便，我们先引入几个符号：SSt表示数据的总变异（即总平方和）SSb表示组间变异（即组间平方和），SSw表示组内变异（即组内平方和）。也有人用RSS表本组内变异。RSS为英文residualsumofsquares的缩写，意为“剩余平方和”，因为总平方和等于组间平方和与组内平方和之和，即SSt=SSb＋SSw，所以组内平方和就等于总平方和减去组间平方和之后所剩余的部分：SSW=SSt-SSb。这也说明，我们只要计算出总平方和与组间平方和，两者相减就可得出组内平方和了。

（二）单因素方差分析的步骤

第一步：提出零假设：H0：1=2=···m（即各组数值或各样本所来自的总体的平均值之间没有差异，m表示组数或样本数）。

第二步：设定显著水平。

第三步：计算总平方和SSt。由于SSt反映整个数据的离散情况，所以用下面的公式

式中：

X——全部数据中的每个观测值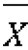； —所有观测值的总平均数。

由于该公式需要从每个观测值中逐个减去总平均数，所以当数据量比较大时，计算起来非常繁琐。

第四步：计算组间平方和SSb。由于SSb反映各组平均数之间的离散情况所以，该式的意思是：把每组的平均数减去总平均数，把所得之差平方，然后乘以所在组的观测值个数，最后再把各组所得的乘积累加起来（这与求总平方和的道理是一样的：把所有数据中的每个观测值与总平均数之差平方，然后再累加。这里，各组的平均数相当于一个个观测值）。为了计算方便，一般用方差估计值通常称为均方（符号为MS，组间均方为MSb，组内均方为MSW，也有人 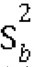和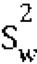 示）。就像方差的通常计算方法一样，我们用组间平方和及组内平方和除以相应的自由度，就可得出组间和组内方差估计值。

由于组间平方和SSb为各组平均数与总平均数之差的平方和，所以组间均方的自由度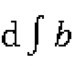（）为组数减1。如用m表示组数（也有用p或k表示的），则其自由度为（m-1）。由于组内平方和SSW为每组的各个观测值与其所在组的平均数之差的平方和，所以组内均方既涉及每组观测值的个数，又涉及组数，因而其自由度（）等于每组观测值个数减1，再乘以组数。如用《表示每组观测值的个数（也有用9表示的），则等于m（n-1）。与SSt相对应的自由度等于组间均方与组内均方自由度之和，即（m-1）＋m（n-1），或mn-1，也即N-1（数据中所有观测值的个数减1）。