逐步回归分析及回归模型检验和分析

一、逐步回归分析

在研究中，事先并不能确定这15个自变量都对因变量都有显著性影响，为从这15个自变量中选择出一些作用较大的因子，建立最优回归方程，我们对上述模型采用前述标准化数据。同时我们通过SPSS软件逐步回归程序进行计算，［45］排除了自变量间的多重线性关系的影响，保留了相对较独立的自变量，求得回归方程是：Y=0.449X1+0.180X4+0.178X3+0.107X15+0.113X2+0.087X7。

二、回归方程的显著性检验和分析

对于求出的回归方程，还需要对其进行显著性检验和分析，对于显著性检验，本文采用拟合优度检验、F检验、T检验；对于回归方程分析，本文采用以及回归方程的残差分析。

（一）回归方程的显著性检验

通过对上述求回归方程过程中的数据统计，得到回归方程的拟合优度检验统计表（见表8-1）、F检验统计表（见表8-2）、T检验统计表（见表8-3）。

表8-1　拟合优度统计表

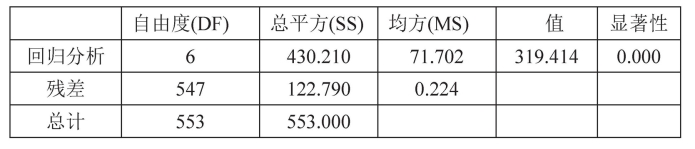
表8-2　F检验统计表

(www.zuozong.com)

表8-3　T检验统计表

对于表8-1，复相关系数R又称相关系数，是用来衡量自变量X与Y之间的相关程度的大小的，表8-1中的复相关系数为0.882，表明自变量X与Y之间的有较高正相关性；决定系数是用来说明自变量解释因变量Y变差的程度的，以测定因变量Y的拟合效果，表8-1中的决定系数为0.778，表明用用自变量可解释因变量变差的77.8%；校正决定系数是调整后的决定系数，表8-1中的校正决定系数为0.776，说明自变量能说明因变量Y的77.6%，因变量Y的22.4%要由其他因素来解释。

对于表8-2和表8-3，F值检验达到了0.01的显著水平，其T值检验中，自变量X1，X4，X3，X15，X2，X7对应的回归系数都达到了大于0.01的显著水平，由此可判定回归方程与各参数检验结果都有显著性意义，所求得的回归方程是有效的。

（二）回归方程的残差分析

残差是预测值与实际值之差的信息，残差图也可用来判断回归模型的拟合效果。图8-1和图8-2是利用SPSS统计软件求回归方程过程中的显示的残差分布实际状况。图1为残差分布的直方图与附于其上的正态分布曲线相比较，可以认为回归方程的残差服从正态分布，满足“残差分布为正态分布”的回归分析假设。图8-2为学生满意度问卷调查的观测量累计概率图，即标准化残差的正态P—P图，用于检验残差分布与正态分布差异的图形。该图的纵坐标为期望累计概率分布，横坐标为观测量累计概率分布，图中的斜线对应着一个均值为0的正态分布，图中的散点密切地散布在这条斜线附近，也验证了随机变量残差服从正态分布，从而证明了数据来自于正态总体。

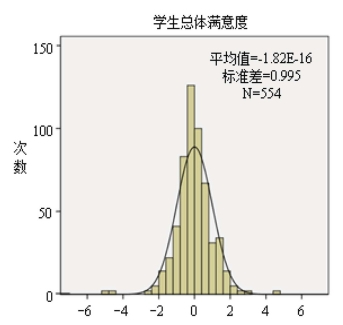
图8-1　残差分布直方图

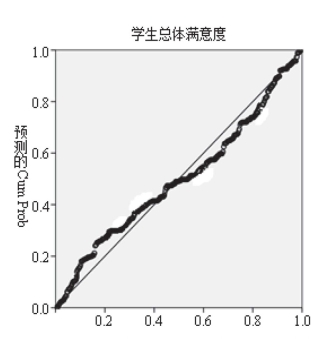
图8-2　回归标准残差的正态P-P图