对称轴（L）的概念和如何使用

第三章　晶体的对称

第一节　对称的概念

对称的现象在自然界和日常生活中极为常见，如植物、动物、某些建筑物、生活用具、器皿等都常呈对称的图形（图3-1）。

图3-1　物体对称示意图

物体或图形对称必须满足两个基本条件：①具有两个或两个以上相同的部分；②这些相同的部分通过一定的操作（如旋转、反映、反伸）可以发生重复。如图3-1中的物体左右两个相等的部分，都可以通过垂直平分它们的镜面的反映而彼此重合。

对称就是物体相同部分有规律的重复。

第二节　晶体对称的特点

晶体是具有对称性的，晶体外形的对称表现为相同的晶面、晶棱和角顶作有规律的重复。晶体的对称和其他物体不同。动植物的对称是长期演化的结果，对称有利于它们的生存。建筑物、工艺品和用具的对称是人为的，是为了使其美观和适用。而晶体的对称是取决于它内在的格子构造，因此，它具有如下特点：

（1）由于晶体内部都具有格子构造，而格子构造本身就是质点在三维空间周期重复的体现，因此，从这种意义上来说，所有晶体都是对称的。

（2）晶体的对称受格子构造规律的限制，也就是说只有符合格子构造规律的对称才能在晶体上体现。因此，晶体的对称是有限的，它遵循“晶体对称定律”（见对称轴一节）。

（3）晶体的对称取决于其内在的本质——格子构造，因此，晶体的对称不仅体现在外形上，同时也体现在物理性质（如光学、力学、热学、电学性质等）上，也就是说晶体的对称不仅包含着几何意义，也包含着物理意义。

晶体的对称性是晶体最重要的特征，晶体的对称性是对种类繁多的晶体进行分类的依据。

第三节　对称要素和对称操作

使物体或图形的相同部分重复出现的操作称为对称操作。在进行对称操作时，总要借助于一些假想的几何要素（点、线、面），如绕直线进行“旋转”操作，对一个平面进行“反映”操作，对一个点进行“反伸”操作。在进行对称操作时所应用的辅助几何要素称为对称要素。

晶体外形可能存在的对称要素和相应的对称操作如下。

一、对称中心（C）

对称中心是晶体内部一个假想的点，通过这一点的直线两端等距离的地方有晶体上相等的部分。所对应的对称操作为反伸。

对称中心用符号C表示。

图3-2是一个具有对称中心的图形，C点为对称中心。在通过C点所作的直线上，距C等距离的两端可以找到对应点，如A和A1，B和B1；也可以看成由A经过C反伸到A1，由B经过C反伸到B1。

一个具有对称中心的图形，其相对应的面、棱、角都体现为反向平行。如图3-3所示，C为对称中心，△ABC与△A′B′C′为反向平行。因此，要确定晶体或晶体模型有无对称中心时，可将晶体模型放在桌子上，看晶体上面是否有一个晶面与下面的晶面（与桌面接触的晶面）平行而且相等。把晶体转动，重复这样的观察，如果晶体上所有的晶面都可以找到与其平行而且相等的晶面，说明晶体有对称中心，否则就没有对称中心。

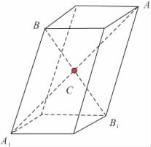
图3-2　具有对称中心的图形

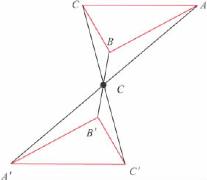
图3-3　由对称中心联系起来的两个反向平行的图形

不是所有晶体都有对称中心，晶体外形上若有对称中心，只可能有一个。

二、对称面（P）

对称面是一个假想的平面，它把晶体平分为互为镜像的两个相等部分。其对称操作是对一个平面的反映。“反映操作”可与“反伸操作”对比，两者不同之处仅在于反伸凭借一个点，反映凭借一个面。

图3-4（a）中P1和P2都是对称面（垂直纸面），因为它们都可以把图形ABDE分成两个互为镜像的相等部分。图3-4（b）中的AD却不是图形ABDE的对称面，因为它虽然把图形ABDE平分为△AED和△ABD两个相等部分，但这两个相等部分不是互为镜像关系，△AED的镜像是△AE1D。

在晶体上对称面的出露位置：

（1）垂直平分晶面（图3-5中1、2、3对称面）。

（2）垂直平分晶棱（图3-5中1、2、3对称面）。

（3）包含晶棱并平分晶面的夹角（图3-5中4、5、6、7、8、9对称面）。

在一个晶体上，可以没有对称面，也可以有一个或若干个对称面，但最多可达9个，如立方体有9个对称面（图3-5），记作9P。

图3-4　对称面和非对称面对比

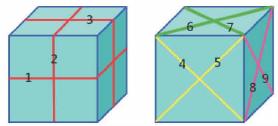
图3-5　晶体上对称面的出露位置

三、对称轴（Ln）

对称轴是通过晶体中心的一条假想直线，晶体围绕它旋转一定角度后，晶体的相等部分重复出现。旋转一周重复的次数称为轴次n，重复时所旋转的最小角度称基转角α，两者之间的关系为n＝360°/α。

对称轴以L表示，轴次n写在它的右上角，写作Ln。

晶体外形上可能出现的对称轴如表3-1所列。

表3-1　晶体外形上各种对称轴的符号及作图符号

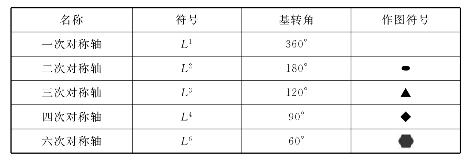
轴次n＞2的对称轴，称高次轴，轴次n≤2的称低次轴。

图3-6为分别具有L2，L3，L4，L6的单锥体及其断面，从图中可以看出，这些锥体绕轴旋转一定基转角后，相同的角顶、晶面和晶棱均重复出现。如具L4的四方单锥，绕L4旋转90°后，锥体上相等部分就重复出现，绕L4旋转360°，相等部分就出现4次。

晶体中对称轴可能出露的位置：

（1）晶面的中心：两相对晶面中心的连线［图3-7（a）］。

（2）晶棱的中点：两相对晶棱中点的连线［图3-7（b）］。

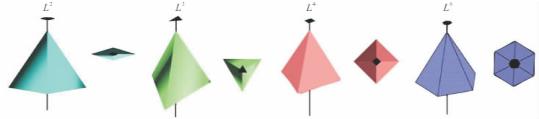
图3-6　晶体中的对称轴L2，L3，L4，L6

（3）角顶上：两相对角顶的连线［图3-7（c）］；或者一个角顶和与之相对的一个晶面中心的连线［图3-7（d）］。

图3-7　对称轴在晶体上的出露位置

由于晶体是具有格子构造的固体物质，这种质点格子状的分布特点决定了晶体的对称轴只有L1，L2，L3，L4，L6这五种，不可能存在五次轴及高于六次的对称轴。这就是晶体对称定律。

晶体对称定律可以这样理解：在晶体结构中，垂直对称轴一定有面网存在，在垂直对称轴的面网上，结点分布所形成的网孔一定要符合对称轴的对称规律。围绕L2，L3，L4，L6所形成的多边形网孔［图3-8（a），（b），（c），（e）］，可以毫无间隙地布满整个平面，从能量上看是稳定的；且这些多边形网孔也符合面网上结点所围成的网孔（即形成平行四边形状）。但围绕L5所形成的正五边形网孔以及围绕高于六次轴所形成的正多边形网孔（如正八边形等）［图3-8（d），（f）］都不能毫无间隙地布满整个平面，从能量上看是不稳定的；且这些多边形网孔大多数不符合面网上结点所围成的网孔。所以，在晶体中不可能存在五次及高于六次的对称轴。

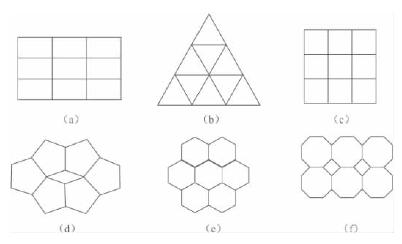
图3-8　垂直对称轴所形成的多边形网孔
（引自潘兆橹等，1993）

四、旋转反伸轴

旋转反伸轴是晶体中的一根假想直线，晶体围绕此直线旋转一定角度后，再对此直线上的一个点进行反伸，可使晶体上相等的部分重复。其对称操作是围绕一根直线的旋转和对此直线上一个点的反伸。

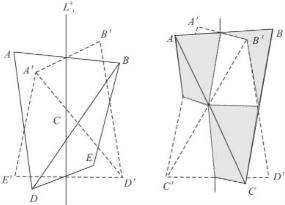
图3-9　具有的四方四面体（引自潘兆橹等，1993）

旋转反伸轴以符号表示，i是反伸之意，n为轴次，n可为1、2、3、4、6。现以为例来加以说明。图3-9所画的结晶多面体为四方四面体，当其绕旋转90°后，角顶A、B、E、D到达A′、B′、E′、D′的位置，再对上的一点C进行反伸，使A′、B′、E′、D′分别与旋转前的D、E、B、A相重合，整个图形重复为旋转前的形象。为了便于理解，也可以就一个晶面来分析，如晶面ABD绕 旋转90°到达A′B′D′位置，再经 上的一点C的反伸，与旋转前的一个晶面DEA重合，其他晶面依此类推，整个晶体重复为原来的形象，旋转360°重复4次。旋转反伸轴的作用如图3-10所示。除外，其余各种旋转反伸轴都可以用其他简单的对称要素或它们的组合来代替，其间关系如下（图3-10）：

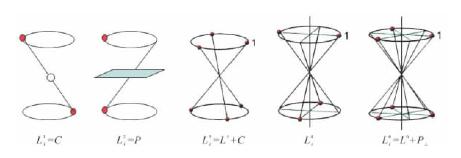
图3-10　各种旋转反伸轴图解
（引自潘兆橹等，1993）

第四节　对称要素组合

在结晶多面体中，可以只有一个对称要素单独存在，也可以有若干个对称要素组合在一起。

对称要素的组合服从以下定理。

定理一：如果有一个二次轴L2垂直n次轴Ln，则必有n个L2垂直Ln。即：Ln＋L2⊥→LnnL2

例如：L2＋→L22L2，L3＋→L33L2，L4＋→L44L2，L6＋→L66L2（图3-11）

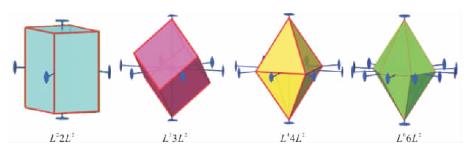
图3-11　定理一图解

定理二：如果有一个对称面P垂直偶次对称轴Ln（偶），则在其交点存在对称中心。即：Ln（偶）＋P⊥→LnPC

例如：L2＋P⊥→L2　PC，L4＋P⊥→L4　PC，L6＋P⊥→L6　PC（图3-12）。

(www.zuozong.com)

图3-12　定理二图解

定理三：如果有一个对称面P包含Ln，则必有n个对称面包含Ln。即：Ln＋P∥→LnnP

例如：L2＋P∥→L22P，L3＋P∥→L33P，L4＋P∥→L44P，L6＋P∥→L66P（图3-13）。

图3-13　定理三图解

定理四：如果有一个二次轴L2垂直于（或者有一个对称面P包含），当n为奇数时则必有n个L2垂直和n个P包含即：当n为偶数时则必有n/2个L2垂直和n/2个P包含即

例如:（图3-14）

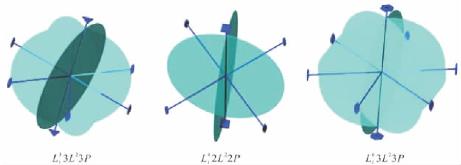
图3-14　定理四图解

第五节　晶体的分类

根据晶体对称特点，可以对晶体进行合理的科学分类。

一、对称型

一个结晶多面体中全部对称要素的总和，称为该结晶多面体的对称型。

晶体上出现哪些对称要素，出现多少，取决于晶体的种类。例如：斜长石和蓝晶石都只有一个对称中心（C）（图3-15），所以斜长石、蓝晶石等只有一个对称中心（C）的晶体都属C这一对称型。又如：石膏、正长石晶体，它们的全部对称要素均为L2PC（图3-16），所以石膏、正长石等均属于L2PC这一对称型的晶体。

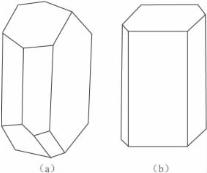
图3-15　只有对称中心（C）的斜长石
（a）和蓝晶石（b）晶体（引自戈定夷等，1989）

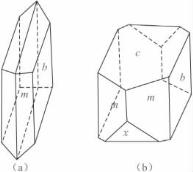
图3-16　具L2PC对称型的石膏（a）和正长石（b）晶体（引自戈定夷等，1989）

根据晶体中可能出现的对称要素种类以及对称要素间组合的规律，从数学上可以推导得出：在一切晶体中，总共只能有32种不同的对称要素组合方式，即32种对称型。无论是天然产出的晶体，还是人工制造的晶体，其对称要素组合都包括在这32个对称型之中，无一例外（表3-2）。

对称型举例如图3-17所示。从中可以看出不同的晶体具有不同的对称型；不同的晶体也可具有相同的对称型，例如立方体和菱形十二面体均具有3L44L36L29PC对称型，四方四面体和复四方偏三角面体均具有对称型。

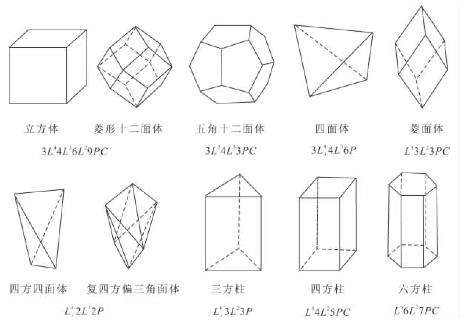
图3-17　对称型举例

二、晶族、晶系及晶类的划分

根据晶体对称的特点可以对晶体进行合理的科学分类。分类依据及分类体系见表3-2。

首先，根据是否有高次轴以及有一个或多个高次轴，把32个对称型归纳为低级、中级和高级3个晶族。

在各晶族中，再根据对称特点划分晶系。晶系共有七个：属于低级晶族的三斜晶系（无对称面和对称轴）、单斜晶系（二次轴和对称面各不多于一个）和斜方晶系（二次轴或对称面多于一个）；属于中级晶族的四方晶系（有一个四次轴）、三方晶系（有一个三次轴）和六方晶系（有一个六次轴）；属于高级晶族的等轴晶系（有四个三次轴）。

表3-2　三十二种对称型及晶体的分类表

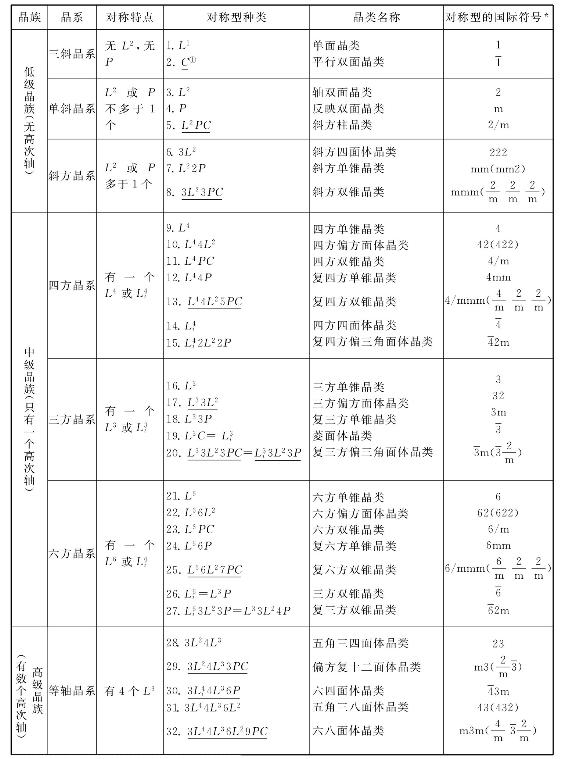
注：①有下划线者为常见的重要对称型。
＊国际符号在本教材没有讲解，可参看《结晶学及矿物学》（潘兆橹等，1993）。

晶体的分类有着重要的实际意义。绝大多数矿物都是晶体。高、中、低三晶族的矿物不仅在形态上各有特点，而且物理性质上也截然不同。七个晶系的矿物在形态和物理性质上也有明显的差异。掌握各晶族、晶系的对称特点，是对矿物进行鉴定和研究必须具备的基础知识。

第六节　十四种空间格子

在第一章中我们已经提出，晶体结构的最基本的特征是质点在三维空间的周期重复，空间格子是表示这种重复规律的几何图形。我们还初步讨论了空间格子的几何要素：结点、行列、面网和平行六面体。

晶体的对称具有表里一致性。晶体外形上的对称，是内部构造对称在晶体形态上的反映。晶体按其对称特点可划分为3个晶族，7个晶系，32个对称型。那么表示晶体内部构造对称规律的几何图形——空间格子有多少种呢？

空间格子的最小重复单位是平行六面体，要弄清楚有多少种空间格子，实质上就是要弄清有多少种平行六面体。

一、平行六面体的选择

对于每一种晶体而言，其结点（相当点）的分布是客观存在的，但平行六面体的选择是人为的。如图3-18所示：同一种结构中其平行六面体的选择可有多种方法。因此，选择平行六面体必须遵循一定的原则才能统一。

平行六面体的选择原则如下。

（1）所选取的平行六面体应能反映结点分布整体所固有的对称性。

（2）在上述前提下，所选取的平行六面体中棱与棱之间的直角关系力求最多。

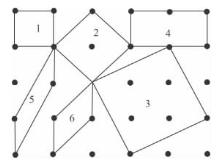
图3-18　平行六面体的选择

（3）在满足以上两个条件的基础上，所选取的平行六面体的体积力求最小。

根据以上原则，分析图3-18所示的情况，点的分布具有四方对称的特点，显然按第1种方法来选取平行六面体才符合上述原则。第2、3种方法有直角关系且符合四方对称，但体积太大；第4种方法虽有直角关系但不符合四方对称；第5、6种方法不符合四方对称且无直角关系。在实际晶体结构中，这种被选取的重复单位（平行六面体）称为晶胞，整个晶体结构就是晶胞在三维空间平行地、毫无间隙地重复堆彻而成（图3-19）。

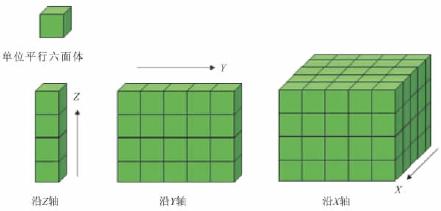
图3-19　平行六面体构成晶体结构图示

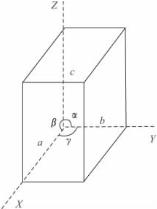
图3-20　决定平行六面体形状和大小的参数

二、各晶系平行六面体的形状和大小

在第二章我们已经知道，平行六面体的形状和大小是由晶胞参数（a、b、c、α、β、γ）决定的，见图3-20。每种晶体都有自己特定的晶胞参数。

根据晶体的对称特点我们不能确定晶胞参数，只能确定晶体常数特点（a、b、c、α、β、γ之间的相对关系）。各晶系对称性不同，因而平行六面体形状也不同（图3-21），晶体常数特点各异。现将7个晶系的晶体常数特点列于表3-3中。

三、平行六面体中结点的分布

在按选择原则选出的平行六面体中，根据结点的分布情况，格子又可分为4种类型（图3-22）。

1.原始格子（P）

结点分布于平行六面体的8个角顶上［图3-22（a）］。

表3-3　七个晶系晶体常数特点

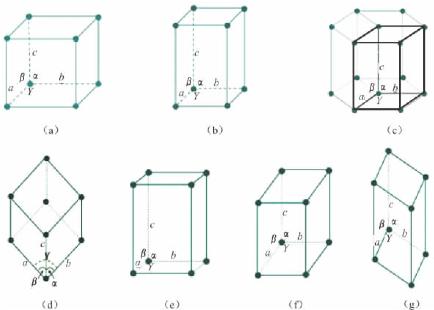
图3-21　七个晶系平行六面体的形状
（a）立方格子；（b）四方格子；（c）六方格子；（d）三方菱面体格子；（e）斜方格子；（f）单斜格子；（g）三斜格子

2.底心格子

结点分布于平行六面体的角顶及一对面的中心。其中又可细分为：①C心格子（C），结点分布于平行六面体的角顶和平行（001）一对面的中心［图3-22 （b）］；②A心格子（A），结点分布于平行六面体的角顶和平行（100）一对面的中心［图3-22（b）］；③B心格子（B），结点分布于平行六面体的角顶和平行（010）一对面的中心［图3-22（b）］。

3.体心格子（I）

结点分布于平行六面体的角顶和体中心［图3-22（c）］。

4.面心格子（F）

结点分布于平行六面体的角顶和面中心［图3-22（d）］。

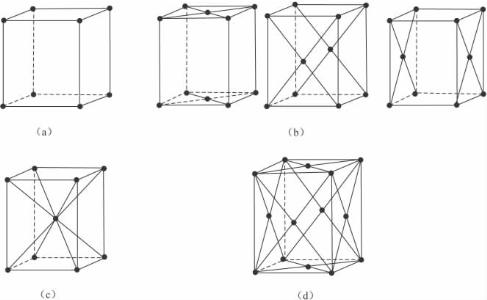
图3-22　4种格子类型
（a）原始格子P；（b）底心格子；（c）体心格子I；（d）面心格子F

四、十四种空间格子（布拉维格子）

前述我们知道平行六面体有7种形状，格子又有四种类型，那么空间格子不是应该有28种吗？其实，空间格子只有14种，它最初是由布拉维推导出来的，所以称为十四种布拉维格子（表3-4）。

表3-4　十四种布拉维格子

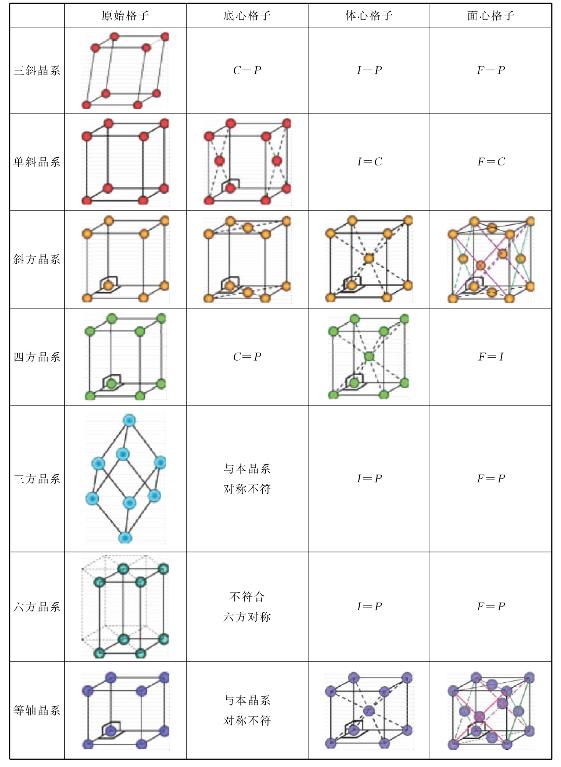
资料来源：引自潘兆橹等，1993。

空间格子之所以只有14种，是因为某些格子类型彼此重复，还有一些不符合某晶系的对称特点而不能在该晶系中存在。如图3-23中：①三斜面心格子（虚线）可以转变成体积更小的三斜原始格子（实线）；②四方底心格子（虚线）可转变为体积更小的四方原始格子（实线）；③三方菱面体面心格子（虚线）可转变为体积更小的三方菱面体原始格子（实线）。而在等轴晶系中，若在立方格子中的一对面的中心安置结点，则完全不符合等轴晶系具有4L3的对称特点，故不可能存在立方底心格子。

因此，当去掉一些重复的、不可能存在的空间格子后，在晶体结构中只可能出现十四种空间格子，即十四种布拉维格子。

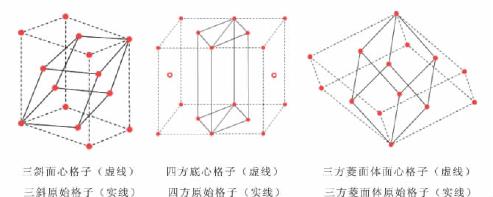
图3-23　格子转换图解（引自潘兆橹等，1993）