晶体及其基本性质是什么呢

第二章　晶体及其基本性质

第一节　晶体的基本概念

自然界到目前为止已经发现了3　000多种矿物，绝大多数是晶体。在古代人们称水晶为晶体，因为水晶有规则的几何多面体外形——比较平整的面、直的棱和尖的棱角［图2-1（a）］。后来在采矿过程中不断发现了更多的和水晶一样具有规则外形的天然矿物，如金刚石、黄铁矿、电气石等［图2-1（b），（c），（d）］，由此对晶体的定义进一步发展，人们认为凡具有几何多面体外形的自然物质均为晶体。

图2-1　石英（水晶）（a）、金刚石（b）、黄铁矿（c）和电气石（d）的晶体

随着生产的发展，科学的不断进步，人们对自然界观察的逐步深入，认识到只把晶体概念定义为规则的几何多面体形态是不准确的。有的晶体形成规则形态，也可以形成不规则的粒状。例如石英：生长于晶洞中的石英多长成规则的多面体形态，即水晶；但也可以呈极不规则形态的颗粒生长于岩石中，像花岗岩中的石英受到生长空间的限制而形成不规则粒状。显然，这种形态上的差异是由生长时的空间条件不同造成的。现代科学实验也证明，把不规则的纯净石英颗粒放入SiO2溶液中，在一定的温度和压力条件下则可形成规则的石英多面体。由此可见，自然多面体形态并非晶体最根本的特征，而是晶体的某种内在本质在一定条件下的外在表现。

什么是晶体的本质呢？有关晶体本质的探讨持续了好几个世纪，直到1912年德国结晶学家劳埃用晶体做光栅使X射线衍射成功，才真正弄清楚了晶体的本质。原来，在一切晶体中，组成它们的物质质点（原子、离子、离子团或分子等）在空间都是作有规律排列的，这种规律主要表现为质点的周期重复，这种质点在三维空间周期性地重复排列称格子构造。因此，我们可以对晶体作出如下定义：

晶体是内部质点（原子、离子或分子）在三维空间周期性重复排列（格子构造）构成的固体物质，或者说晶体是具有格子构造的固体。

数以千计的不同种类晶体，尽管各种晶体的结构各不相同，但都具有格子构造，这是一切晶体的共同属性。

与上述情况相反，有些状似固态的物质，如玻璃、琥珀等，它们的内部质点不作规则排列，即不具格子构造，称为非晶质或非晶质体。图2-2是晶体与玻璃（二者化学成分都是SiO2）的结构示意图，由图可见，晶体内部结构中的质点是有规律排列的，具有格子构造；非晶体的内部结构是无规律的，不具格子构造。

晶体和非晶体在一定的条件下是可以相互转化的。

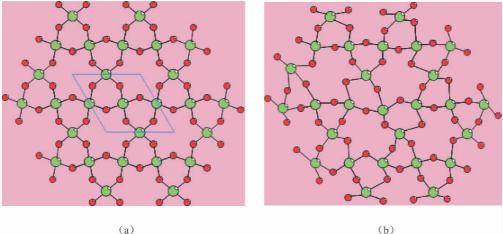
图2-2　晶体和玻璃的结构示意图（引自潘兆橹，1993）
（a）晶体；（b）玻璃

脱玻化作用（结晶化作用）：非晶体自发地转变为质点规则排列的晶体的作用称之为脱玻化作用。自然界，高温岩浆迅速冷却凝固而成的火山玻璃，是非晶体。在漫长的地质年代，火山玻璃内部质点不断地扩散、调整、排列逐渐有序，而形成一些矿物晶体。

玻璃化作用（非晶化作用）：晶体内部质点规则排列遭到破坏而向非晶体转变的作用称之为玻璃化作用。自然界中含放射性元素的结晶矿物，由于受到放射性元素蜕变时发出的α射线作用，晶体遭到破坏，而转变为非晶质的矿物（仍可保持原结晶矿物多面体外形的假象）。

第二节　空间格子

晶体内部结构的最基本特征是质点在三维空间作有规律的周期重复，表示晶体内部结构中质点重复规律的几何图形，就是空间格子。

一、导出空间格子的方法

要从晶体结构中导出空间格子，必须找出晶体结构中的相当点，再将相当点按照一定的规律连接起来就形成了空间格子。相当点必须满足两个条件：

（1）点的内容（或种类）相同。

（2）点的周围环境相同。

如图2-3所示，每种颜色点的种类相同，点周围的环境也相同，因此，每种颜色的点都可以看做晶体结构中的相当点。

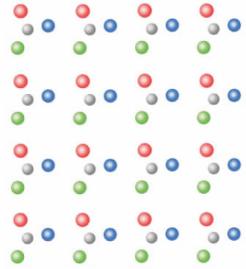
图2-3　晶体结构中的相当点

下面我们以石盐NaCl为例，说明空间格子如何导出。

先看一维图案（图2-4）。

A-NaCl中沿Y轴Na＋和Cl-排列的情况。

B-以Na＋为相当点，它满足相当点的两个条件，将这些相当点抽取出来沿直线排列。

C-抽象为直线点阵。

二维图案（图2-5）。

（a）-NaCl中XY平面Na＋和Cl-排列的情况。

（b）-以Na＋或Cl-作为相当点，并将其从晶体结构中抽取出来，将它们在平面上按一定规则排列。

（c）-抽象为平面点阵。

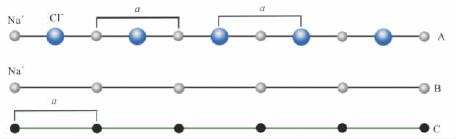
图2-4　相当点一维导出图案

图2-5　相当点二维导出图案

三维图案（图2-6）：

（a）—NaCl中Na＋和Cl-在三维空间的排列情况。

图2-6　相当点三维导出图案

（b）—以Na＋或Cl-作为相当点，并将其从晶体结构中抽取出来，抽象为空间点阵，即形成了空间格子。

任何复杂的晶体结构，只要找出相当点，抽象出空间格子，复杂晶体结构的重复规律就变得一目了然。

空间格子与具体的晶体结构是什么关系？可以认为具体的晶体结构是由多套空间格子组成的。

具体的晶体结构是多种原子、离子组成的，使得其重复规律不容易看出来，而空间格子就是使其重复规律突出表现出来。空间格子仅仅是一个体现晶体结构中的周期重复规律的几何图形，比具体晶体结构要简单得多（图2-7）。

图2-7　晶体结构和空间格子关系
（a）晶体结构；（b）空间格子

二、空间格子的几何要素

1.结点(www.zuozong.com)

是空间格子中的点，代表晶体结构中的相当点。在实际的晶体结构中结点可以为相同的离子、原子或分子所占据，但实际晶体中的同种质点却并不一定只占据在同一套结点上。在空间格子中，就结点本身而言，它们并不代表任何质点，它们只有几何意义，为几何点（图2-8）。

2.行列

结点在直线上的排列即构成行列。空间格子中任意二结点联结起来的直线就是一条行列（图2-9中的AB）。行列中相邻结点间的距离称为该行列的结点间距（图2-9中的a）。在同一行列中结点间距是相等的（图2-9中的AC＝CB），在平行的行列上结点间距也是相等的（图2-9中的AD＝BE）；不同方向的行列，其结点间距一般是不等的，某些方向的行列上结点分布较密，而另一些则较稀。

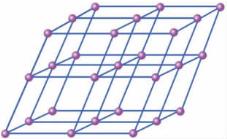
图2-8　结点示意图

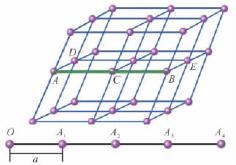
图2-9　行列与结点间距示意图

3.面网

结点在平面上的分布即构成面网（图2-10中的ABCD即为一个面网）。空间格子中不在同一行列上的任意3个结点就可联结成一个面网，换句话说，也就是任意两个相交的行列就可决定一个面网。面网上单位面积内结点的密度称为面网密度。相互平行的面网，面网密度必相同，且任意两相邻面网间的垂直距离——面网间距（图2-11中的AB）也必定相等；互不平行的面网，面网密度及面网间距一般不同。面网密度大的面网其面网间距也大，反之，面网密度小，面网间距也小，如图2-12所示，其中AA′，BB′，CC′，DD′的面网密度依次减小，它们的面网间距d1，d2，d3，d4也依次减小。

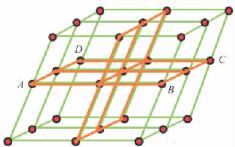
图2-10　面网示意图

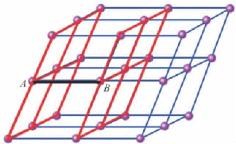
图2-11　面网间距示意图

4.平行六面体

空间格子的最小重复单位或结点在三维空间形成的最小单位，即平行六面体。它由六个两两平行而且相等的面组成。实际晶体结构中这样划分出来的最小单位称为晶胞。空间格子可视为由平行六面体在三维空间平行、毫无间隙地重复堆砌而成的。同样整个晶体结构可以视为晶胞在三维空间平行、毫无间隙地重复堆砌。晶胞的形状和大小则取决于它的三条彼此相交的棱的长度（图2-13中的a、b、c）和它们之间的夹角（图2-13中的α、β、γ）。

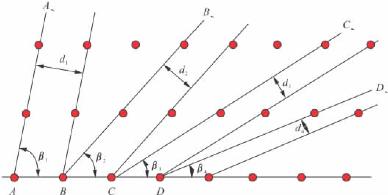
图2-12　面网密度与面网间距关系示意图（引自罗谷风等，1985）

图2-13　平行六面体示意图
（a）空间格子；（b）平行六面体

第三节　晶体的基本性质

一、均一性

由于晶体是具有格子构造的固体，在同一晶体的各个不同部分，质点的分布是一样的，所以晶体的各个部分的物理性质和化学性质也是相同的，这就是晶体的均一性。如将一块纯净的水晶打碎，每一块的成分都是SiO2、密度都是2.65g/cm3。

必须注意的是：非晶质体也具均一性，如玻璃的不同部分折射率、膨胀系数、热导率等都是相同的。但是由于非晶质体的质点排列不具格子构造，所以其均一性是统计的、平均近似的均一，称为统计均一性；而晶体的均一性是由其格子构造决定的，称为结晶均一性。液体和气体也具有统计均一性。

二、自限性

晶体在适当条件下可以自发地形成几何多面体外形的性质，这种性质叫自限性，如图2-14所示。

图2-14　晶体自限性示意图
（a）水晶的柱状晶体；（b）黄铁矿的立方体晶体

晶体为平的晶面所包围，晶面相交成直的晶棱，晶棱会聚成尖的角顶。晶体的多面体形态是其内部格子构造在外形上的直接反映。晶面、晶棱和角顶分别与格子构造中的面网、行列和结点相对应，它们之间的关系如图2-15所示。

晶面：晶体表面上自发长成的平面。

晶棱：晶面的交棱。角顶：晶棱会聚的点。

三、异向性（各向异性）

在同一格子构造中，在不同方向上质点排列一般是不一样的，因此，晶体的性质随方向的不同而有所差异，这就是晶体的异向性。如蓝晶石的硬度随方向不同有显著差别，平行晶体延长方向（图2-16中的AA方向）硬度小于小刀，垂直晶体延长方向（图2-16中的BB方向）硬度大于小刀，因此蓝晶石又名二硬石。又如云母、方解石等矿物晶体具有完好的解理，受力后可沿晶体的一定方向裂开成光滑的平面，而沿其他方向则不能裂开成光滑的平面。在矿物晶体的力学、光学、热学、电学等性质中，都有明显的异向性的体现。此外，如晶体的多面体形态，也是其异向性的一种表现，无异向性的外形应该是球形。非晶质体一般表现为等向性，其性质一般不随方向而改变。

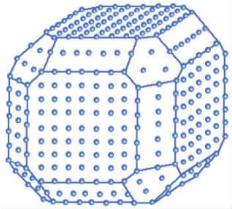
图2-15　晶面、晶棱、角顶与面网、行列、结点的关系示意图
（引自潘兆橹等，1993）

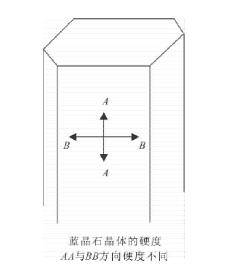
图2-16　蓝晶石晶体硬度的异向性
（引自潘兆橹等，1993）

四、对称性

晶体具异向性，但这并不排斥晶体在某些特定的方向上具有相同的性质。晶体的相同部分（如外形上的相同晶面、晶棱或角顶，内部结构中的相同面网、行列或质点等）能够在不同的方向或位置上有规律地重复出现，这就是晶体的对称性。晶体的格子构造本身就是质点重复规律的体现，对称性是晶体极其重要的性质，是晶体分类的基础，我们将在第三章中详加讨论。

五、最小内能性

在相同的热力学条件下，晶体与其同种物质的气体、液体和非晶质体相比较，其内能最小，这就是晶体的最小内能性。所谓内能，包括质点的动能与势能。例如，冰是一种晶体，它的内能比水和水蒸气小，当水的温度逐渐下降，在常压下降至摄氏零度时，水就开始结冰，由液体状态转变为固体状态，此时温度就停止下降了，当水转化为冰后，温度还可以下降。温度下降的停顿是因为水分子由无规则状态转变为有规律排列的结晶格子时，伴随有能量的析出。因此，在一定温度和压力下，晶体与成分相同但处于其他状态的物体比较，具有最小内能。

动能与物体所处的热力学条件有关，温度越高，质点的热运动越强，动能也就越大，因此它不能直接用来比较物体间内能的大小。可用来比较内能大小的只有势能，势能取决于质点间的距离与排列。

晶体是具有格子构造的固体，其内部质点是有规律地排列的，这种规律的排列是质点间的引力与斥力达到平衡的结果。在这种情况下，无论是质点间的距离增大还是缩小，都将导致质点的相对势能的增加。非晶质体、液体、气体由于它们内部质点的排列不是有规律的，质点间的距离不可能是平衡距离，因此它们的势能也较晶体为大。也就是说在相同的热力学条件下，它们的内能都较晶体为大。实验证明：当物体由气态、液态、非晶质状态过渡到结晶状态时，都有热能的析出；相反，晶格的破坏也必然伴随着吸热效应。

当晶体加热时，起初温度是随着时间逐渐上升的，当达到某一温度时晶体开始溶解，同时温度的上升停顿了，此时所加的热量用于破坏晶体的格子构造，直到晶体完全溶解，温度才开始继续上升。在温度停顿的时间内，晶体吸收了一定的热量而使自己转变为液体，这些热量称为溶解潜热。由于晶体的格子构造中各个部分的质点是按同一方式排列的，破坏晶体各个部分需要同样的温度，因此，晶体具有一定的熔点［图2-17（a）］。

非晶质体则与之不同，由于它们不具有格子构造，所以没有一定的熔点。例如，将玻璃加热时，它首先变软，逐渐变为黏稠的熔体。在这一过程中没有温度的停顿，其加热曲线为一光滑的曲线［图2-17（b）］。

六、稳定性

在相同的热力学条件下，晶体比具有相同化学成分的非晶体稳定，非晶质体有自发转变为晶体的必然趋势，而晶体决不会自发地转变为非晶质体，这就是晶体的稳定性。晶体的稳定性是晶体具有最小内能性的必然结果。

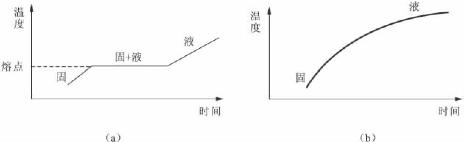
图2-17　晶体与非晶质体的加热曲线示意图
（a）晶体的加热曲线；（b）非晶质体的加热曲线